Search
moon
sun
3️⃣

영상 디스플레이의 기초 [2021/02/08~2021/02/15]

영상에서 화질을 결정하는 두 가지 요소

•
공간 해상도
•
양자화

공간 해상도 (spatial resolution)

🔑
영상에 대한 화소들의 밀도를 공간 해상도라고 한다.

샘플링 (Sampling)

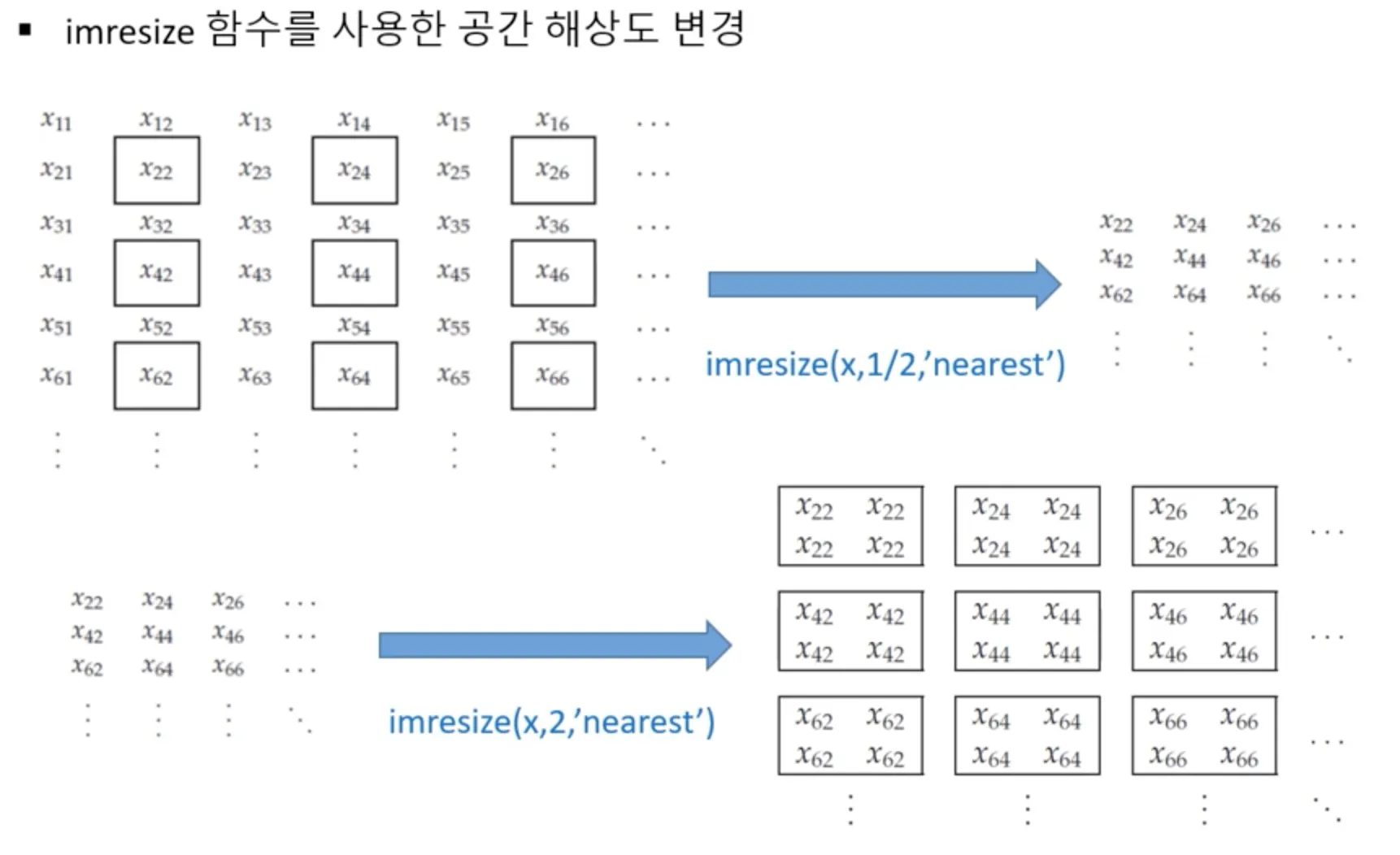
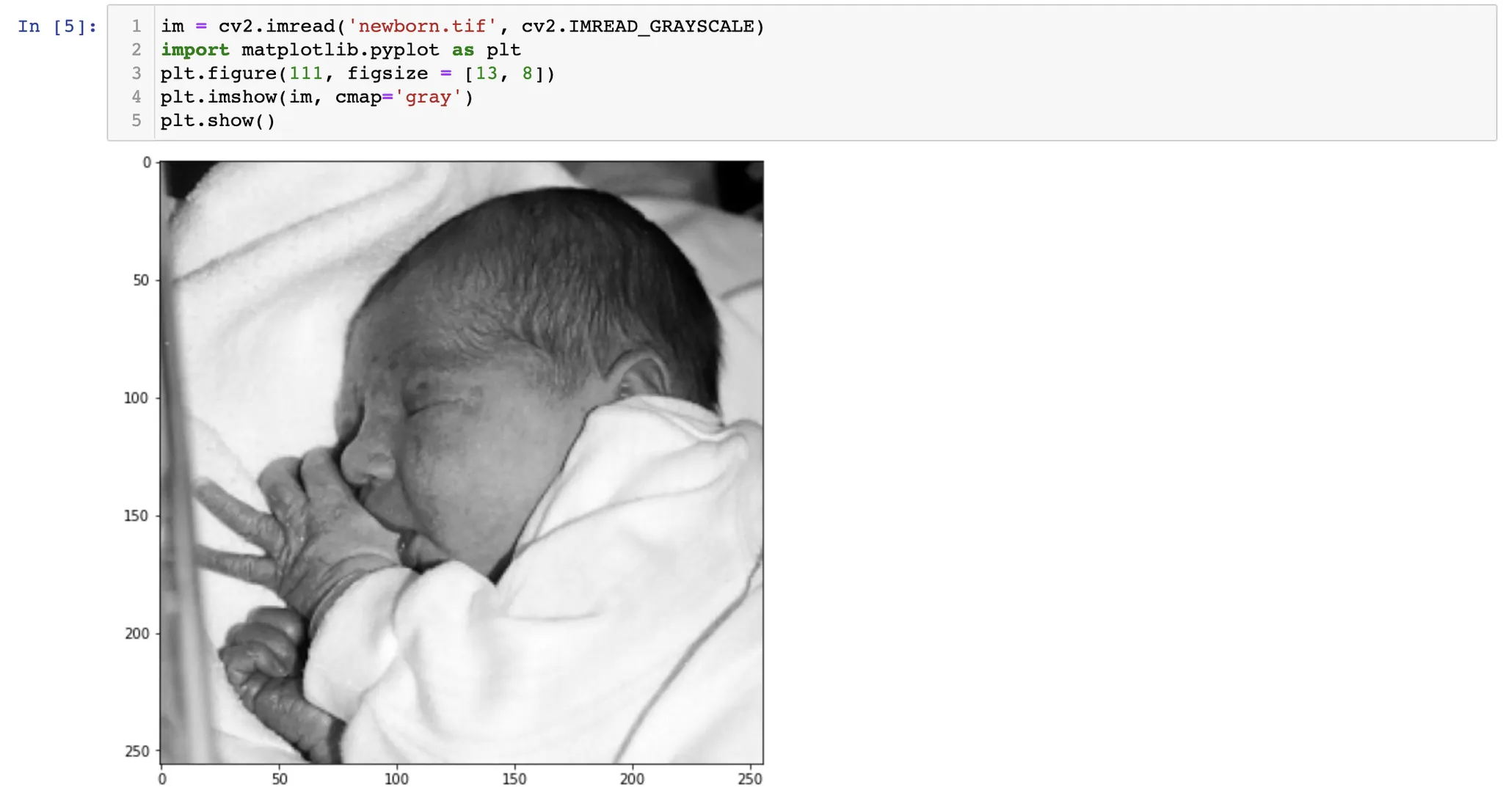
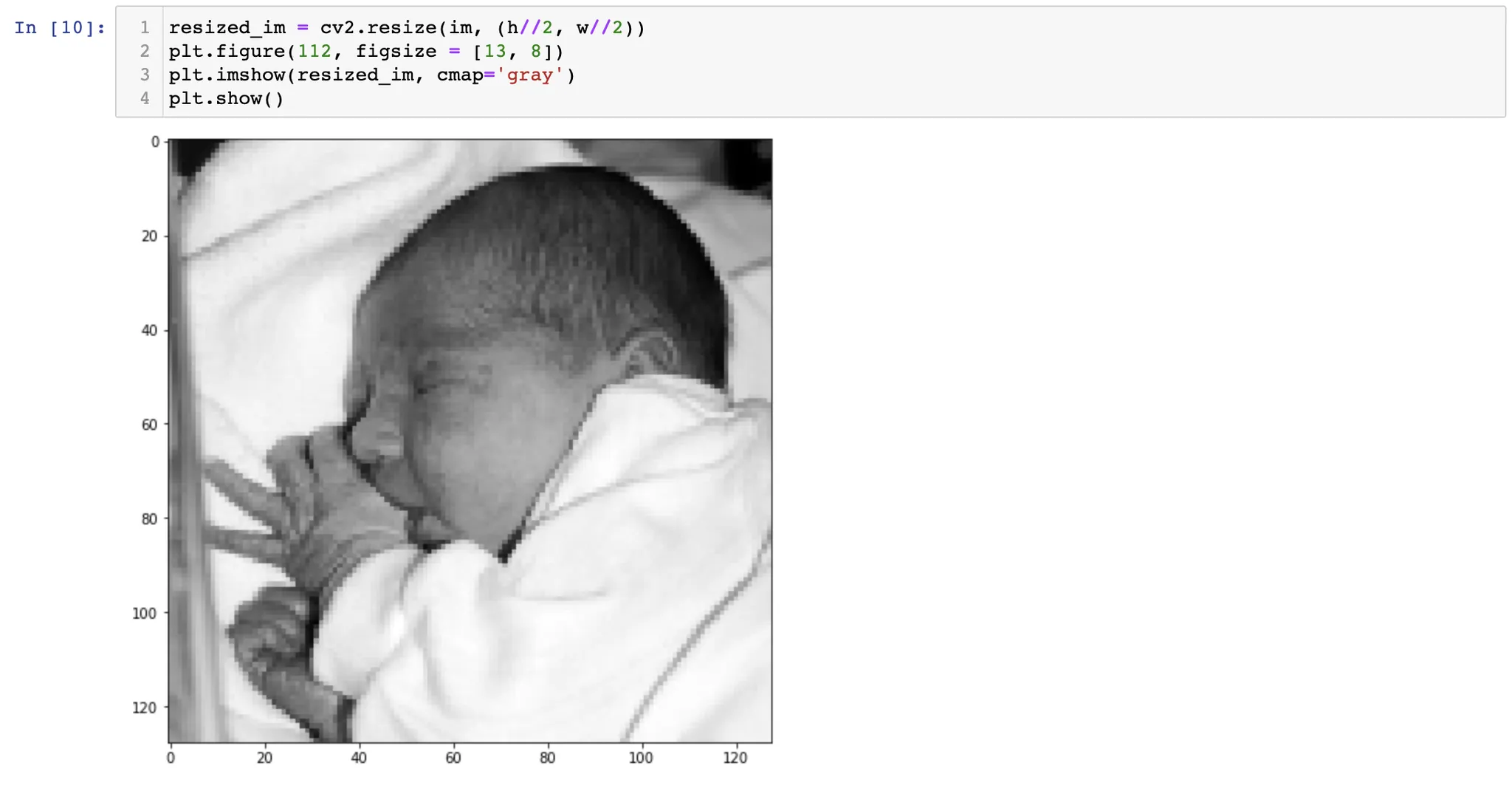
python 에서는 cv2.resize 를 통해 이미지의 공간 해상도를 변경할 수 있다. 위 사진에서는, N by N 이미지를 N/2 by N/2 이미지로 공간 해상도를 줄이고, 이를 다시 N by N 이미지로 공간 해상도를 다시 늘렸다.
💡
입력 영상과 최종 영상의 크기는 같지만, 정보의 양이 다르고, 실제적인 해상도가 다르다. 이러한 실제적인 해상도를 effective resolution 이라고 한다.

블록화 / 화소화 (pixelization)

샘플링을 더 적게 하게 되면 블록화(화소화, pixelization) 현상이 나타나게 된다.

양자화 (quantization)

💡
영상의 밝기 (intensity) 를 표현하는 데 사용되는 밝기값의 개수를 정하고 표현하는 것을 양자화라고 한다.
기본 영상은 256개의 ( = uint8 = 2^8 ) 개의 숫자로 양자화한다. 상황에 따라 256개보다 적은 수의 밝기값으로 양자화할 필요가 있다.

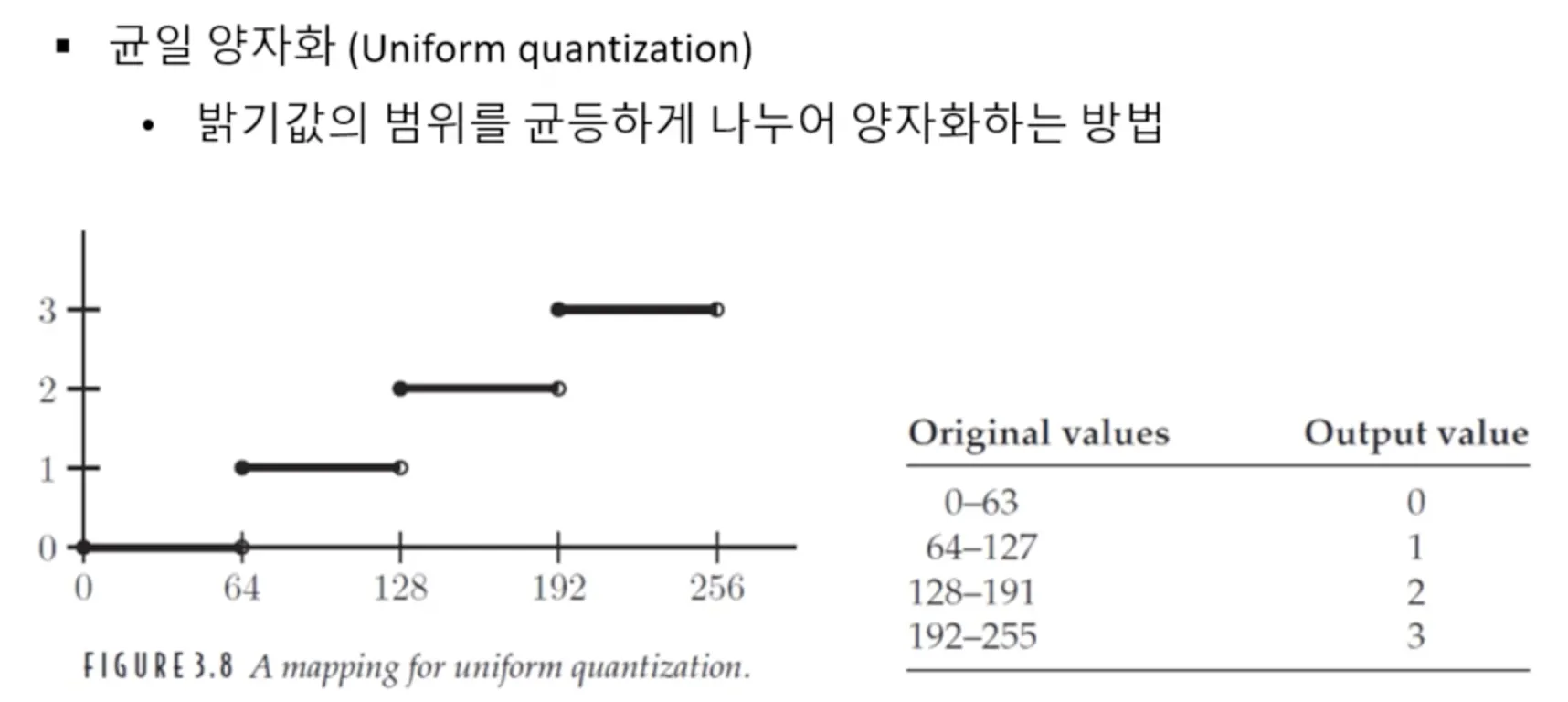
균일 양자화 (uniform quantization)

💡
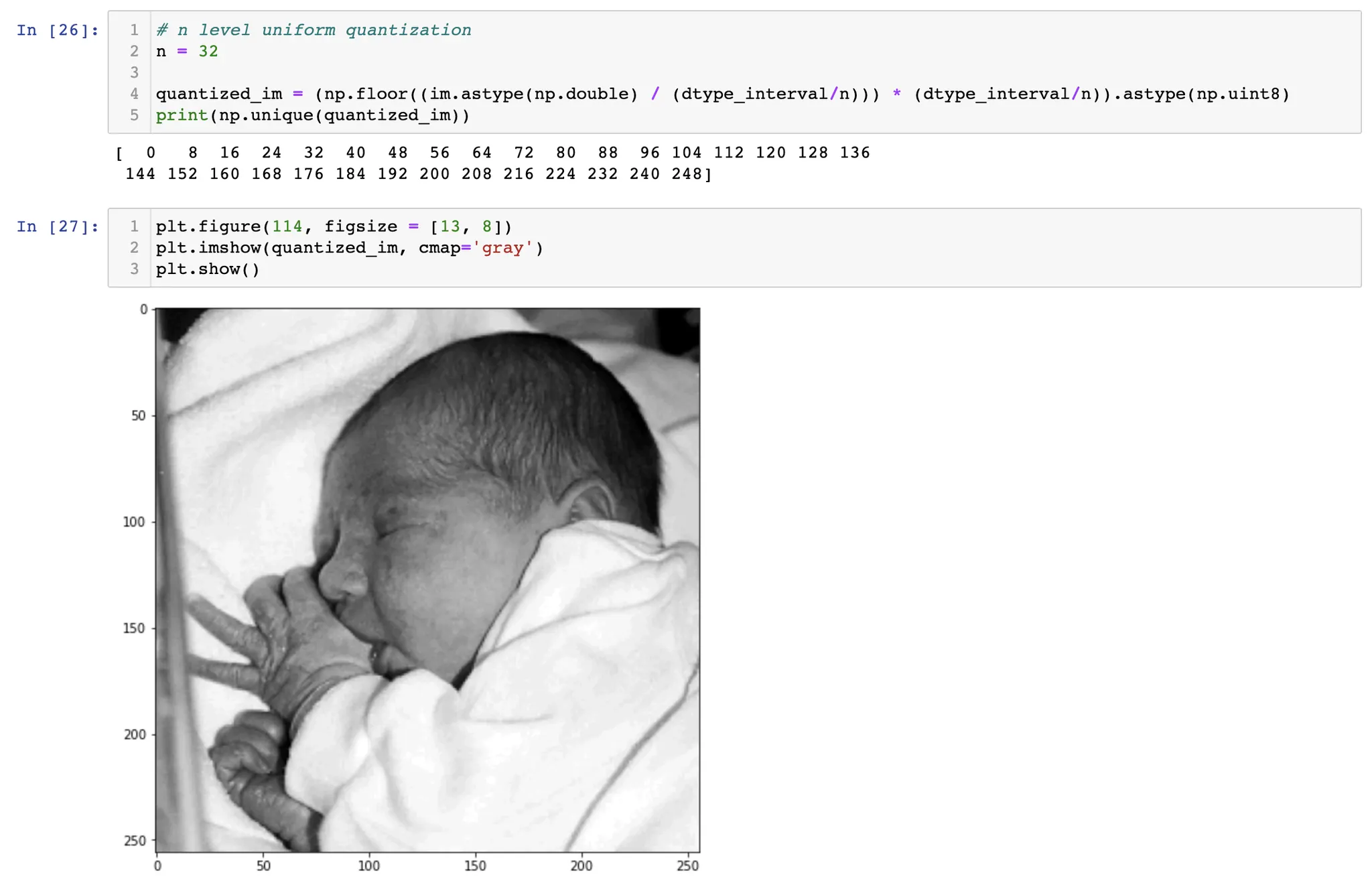
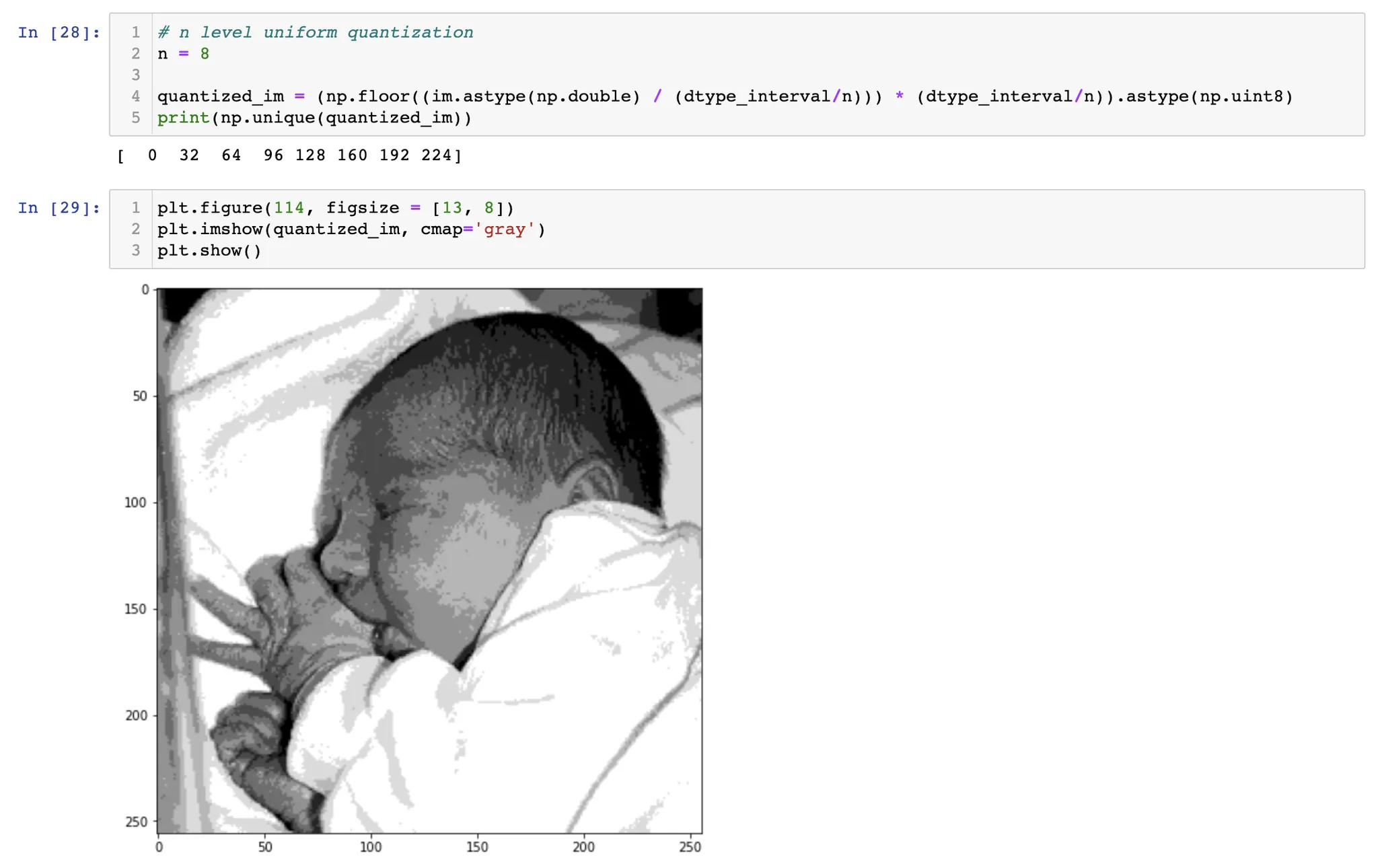
밝기값의 범위를 균등하게 나누어 양자화하는 것을 균일 양자화 (Uniform quantization) 라고 한다.
💡
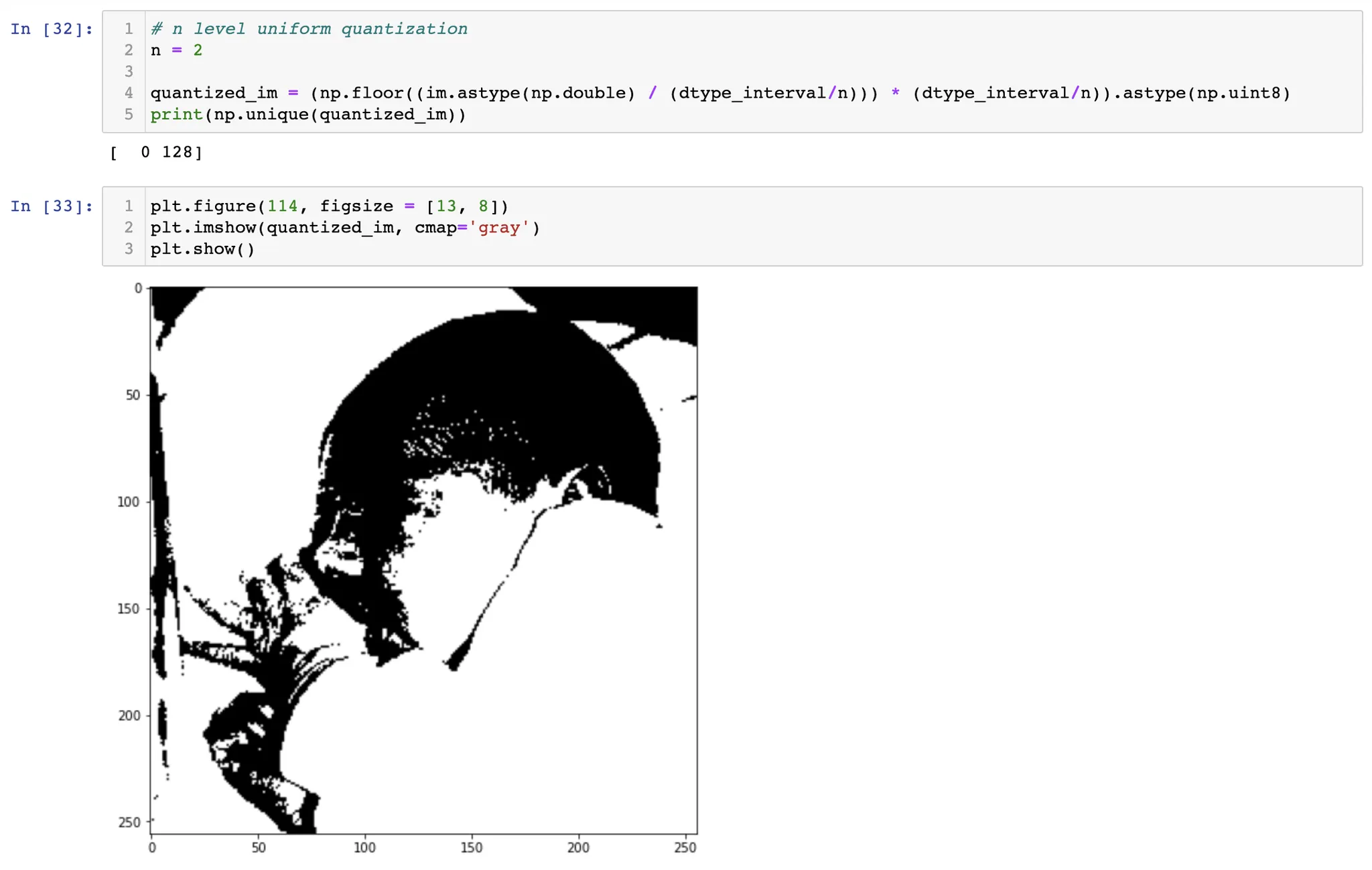
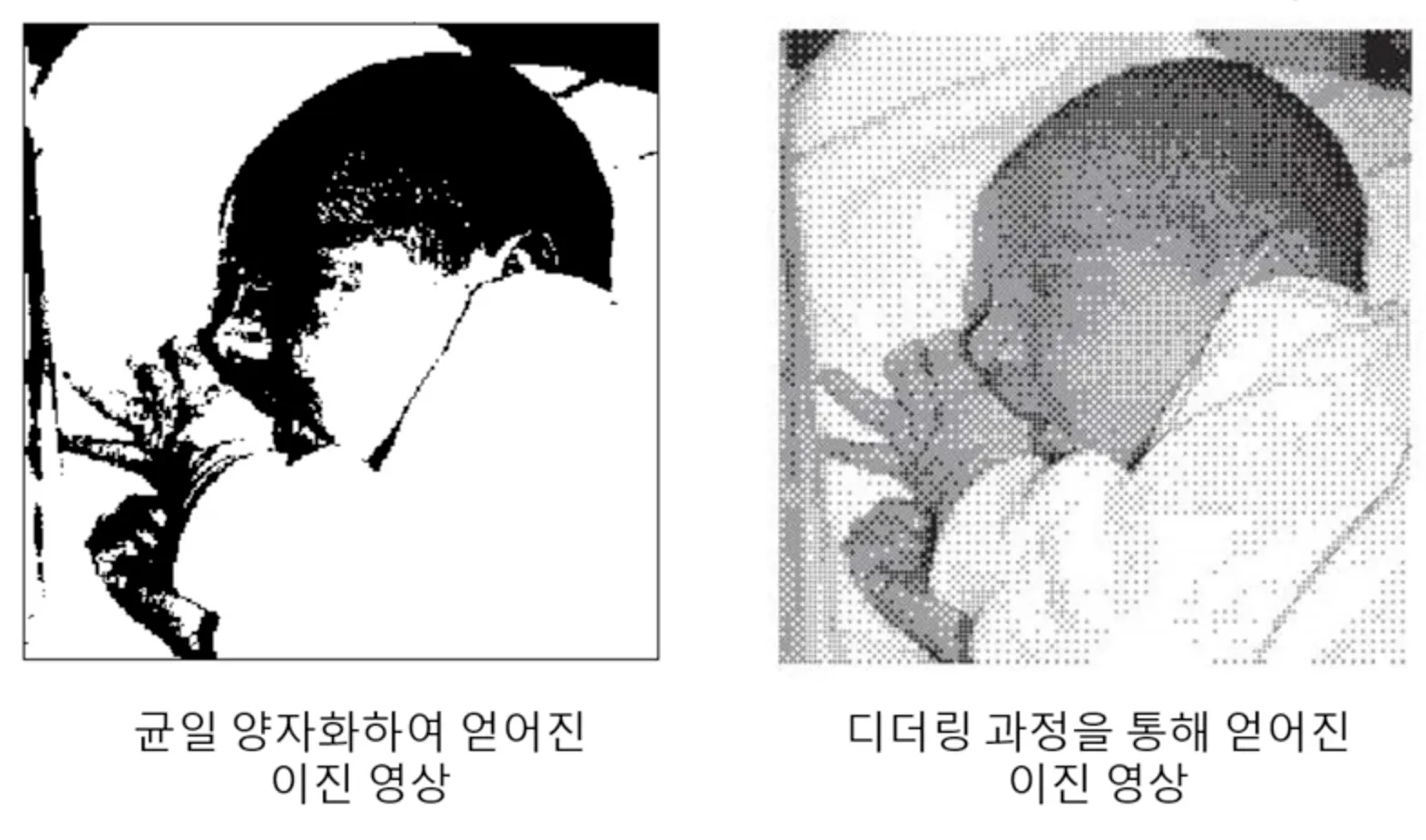
이렇듯, 균일 양자화를 하면, 원 영상에서는 존재한다고 느끼지 못하는 "거짓 윤곽" 이 나타날 수 있다. 이것은 양자화가 더 심하게 될수록 더 극단적으로 나타날 수밖에 없다.

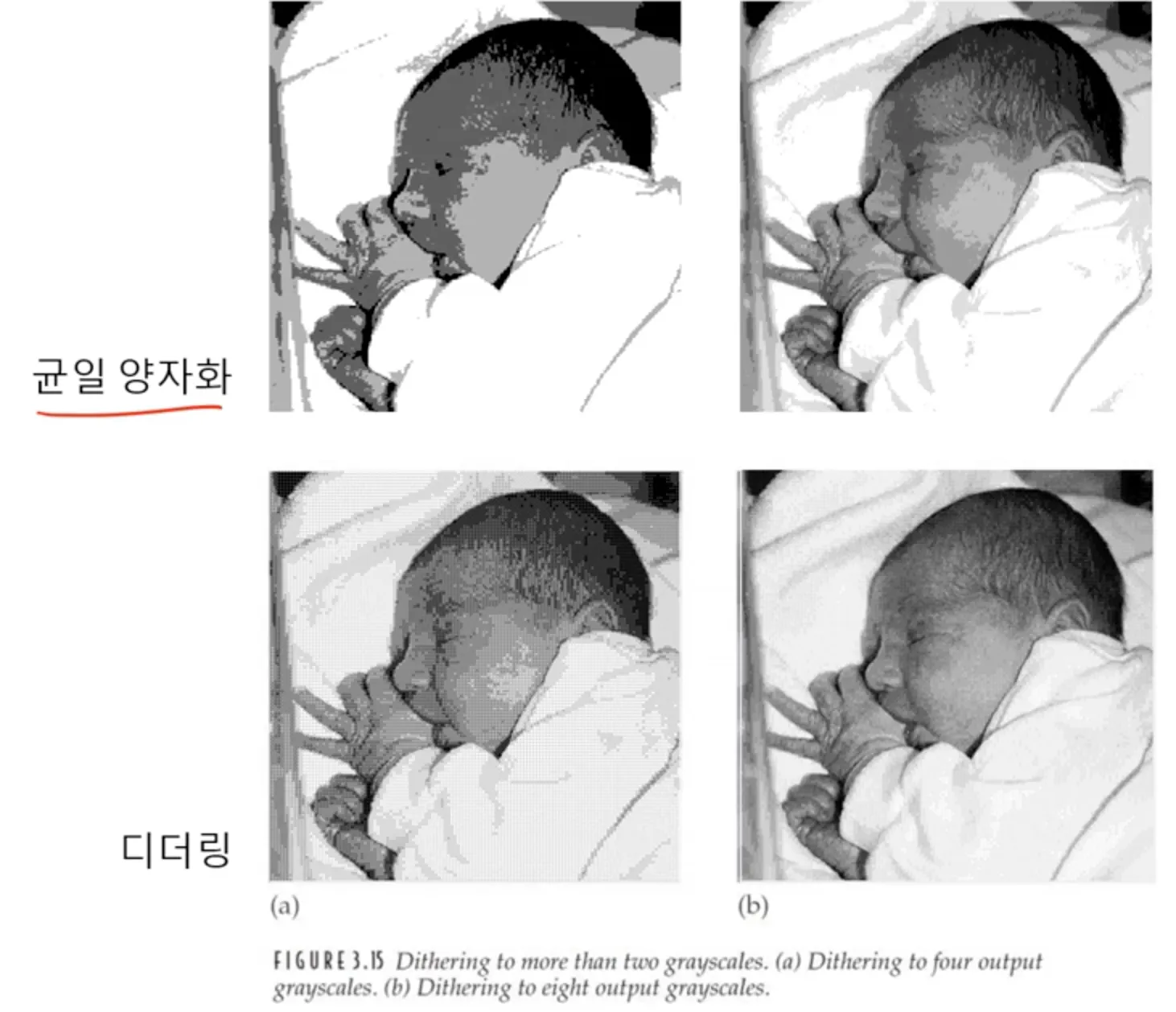
디더링 (Dithering)

🔑
디더링 (dithering) 은 quantization 을 하면서도 영상의 quality 를 떨어뜨리지 않는, 컬러의 수 축소 방법이다.
🔑
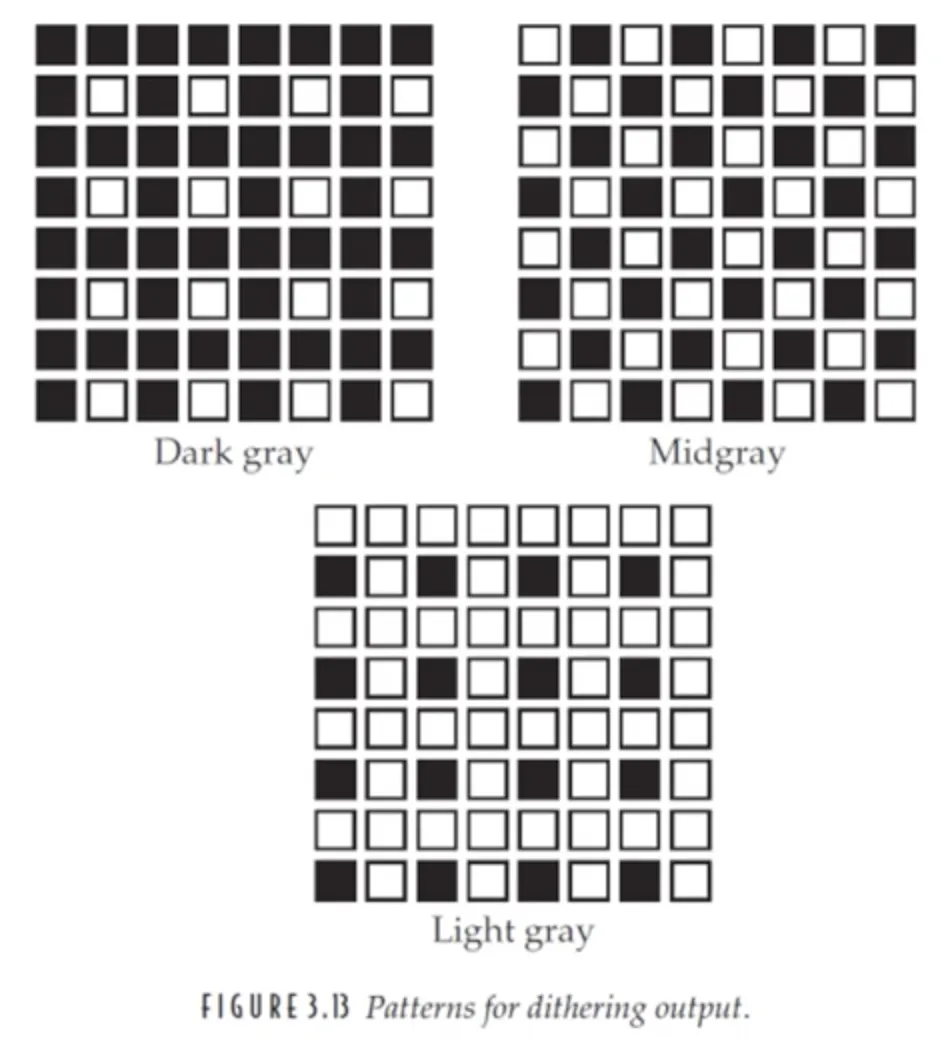
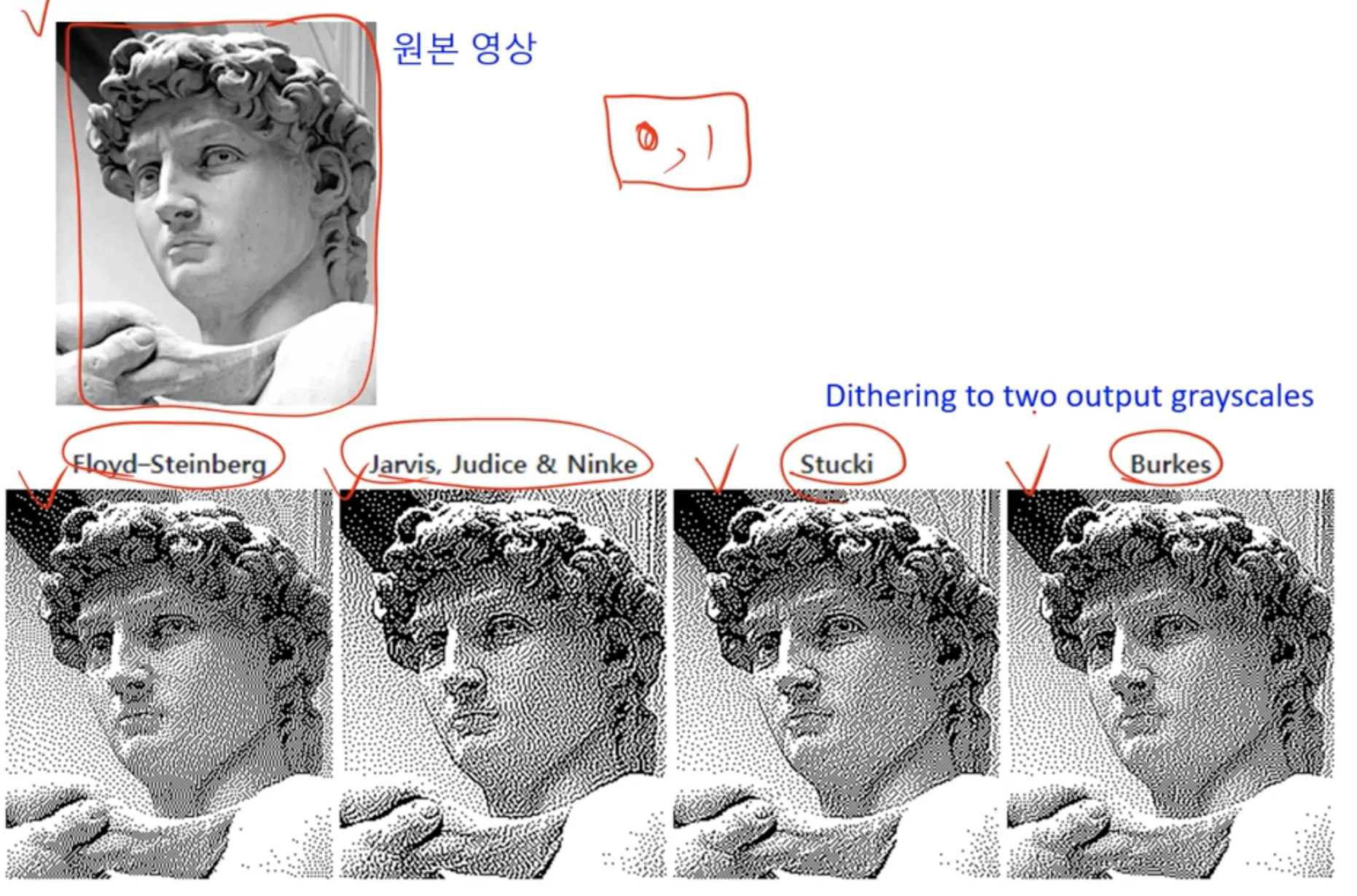
halftoning 은 디더링 (dithering) 의 한 형태로, 영상을 두 가지 톤 (tone) 으로 표현하는 것을 의미한다.
특히, halftoning 은 dithering 의 극단적인 경우로, 영상의 밝기값을 0, 1 로만 양자화해야 한다. 하지만 균일한 양자화는 앞서 보았듯 거짓 윤곽이 정말 많이 나타난다. 이를 해결하는 방법을 알아보자.
우선, 패턴 처리를 활용한 방법이다. 위 그림처럼, 하나의 화소가 아닌 영역의 밝기에 따라 흑과 백 두 톤의 픽셀비율을 조절하는 방법을 상상할 수 있다.
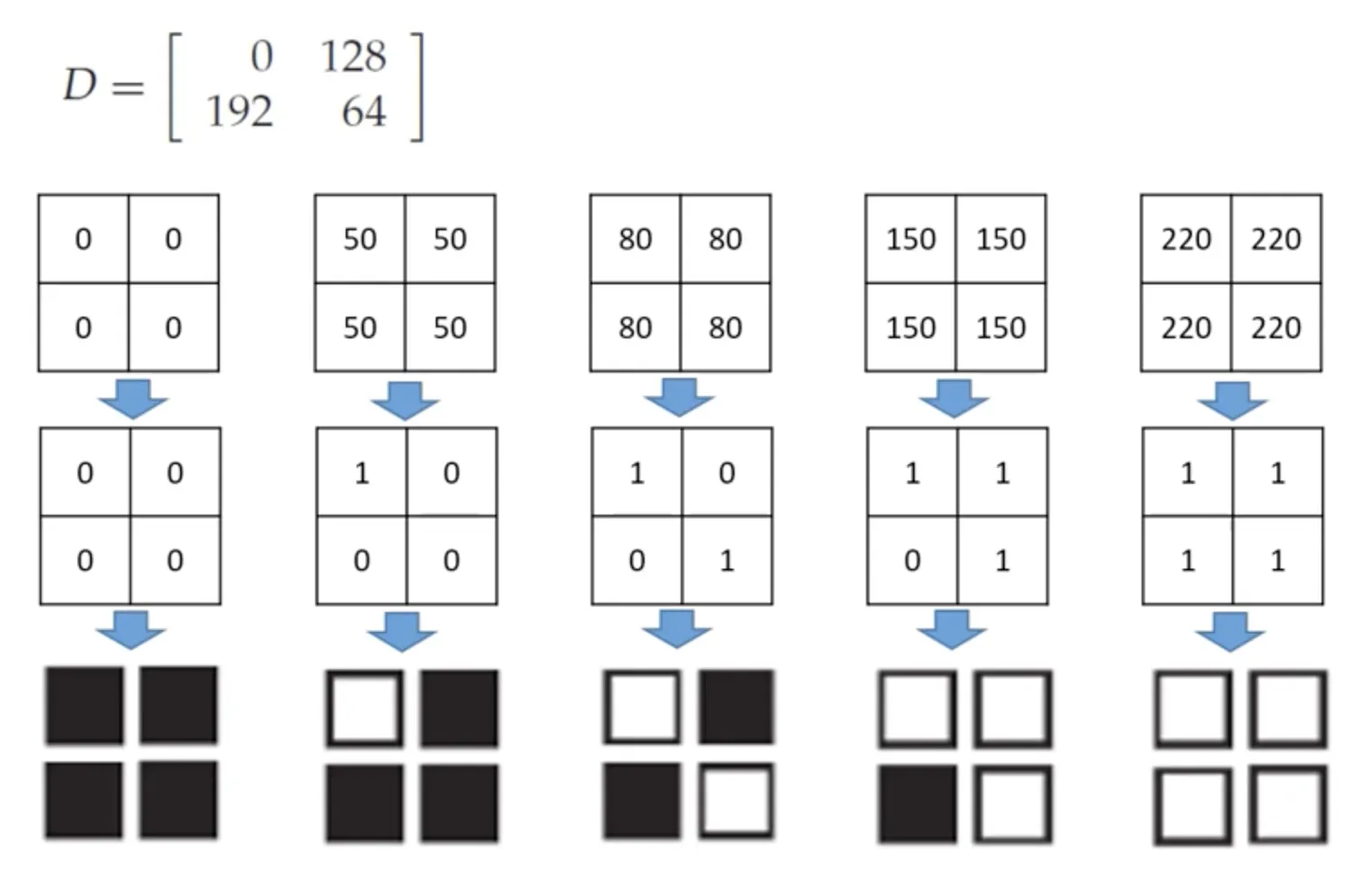
강의에서는 이것을 달성하기 위한 방법들 중, 아주 간단한 방법을 소개한다고 한다. 강의에서 소개한 방법은 dithering matrix 을 통한 방법이다.
갑자기 행렬이 나와서 당황스러울 수 있지만, 결국 그냥 네 픽셀과 행렬의 네 요소를 비교해서 크면 1, 작으면 0 을 그 위치에 대입하겠다는 것이다.
n = 4 dithering_4 = np.linspace(uint8_min, uint8_max, n).astype(np.uint8) print(dithering_4) dithering_4_mat = dithering_4.reshape([np.sqrt(n).astype(np.uint8), np.sqrt(n).astype(np.uint8)]) print(dithering_4_mat)
Python
복사
[ 0 85 170 255] [[ 0 85] [170 255]]
Python
복사
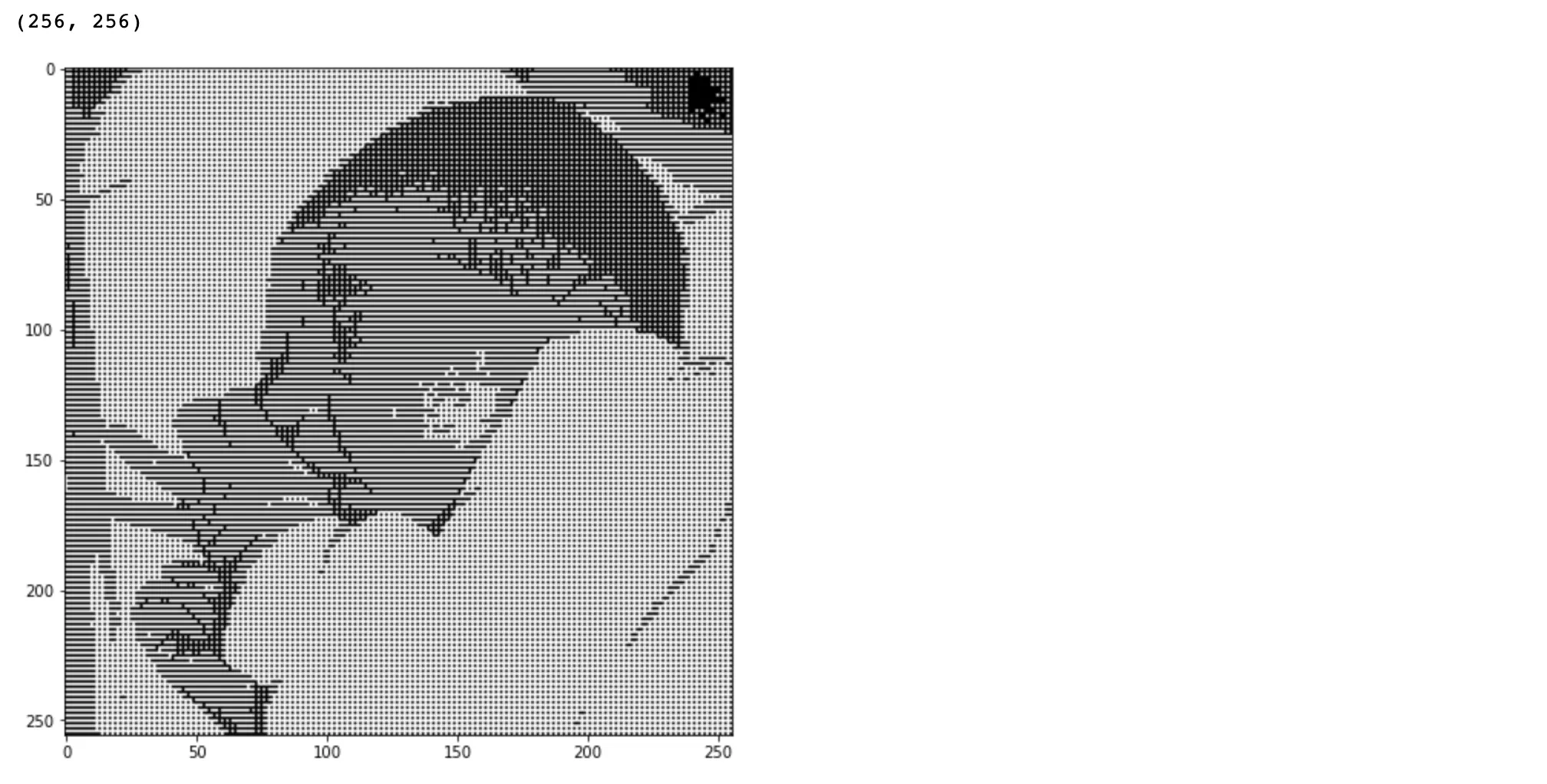
n = 4 dithering_4_mat = np.tile(dithering_4_mat, [h//np.sqrt(n).astype(np.uint8), w//np.sqrt(n).astype(np.uint8)]) print(dithering_4_mat.shape) dithering_4_im = (im > dithering_4_mat) plt.figure(121, figsize = [13, 8]) plt.imshow(dithering_4_im, cmap='gray') plt.show()
Python
복사
좋은 디더링 알고리즘을 사용하면 아래와 같이 더욱 디테일한 영상을 만들어 볼 수 있다.
이제 n-output grayscale dithering 을 해 보자.
💡
dithering 의 한 형태인 halfolding 은 binary 형태로 나타내는 것을 의미하므로, 다음에 시도해볼 내용은 halfolding 이 아니기 때문에 0 과 1 만으로 이루어져 있지는 않다.
4-output grayscale dithering 은 다음과 같은 과정으로 이루어진다.
q(i,j)=floor(x(i,j)/85)q(i,j) = floor(x(i,j)/85)
이때, 85 라는 값은 85=ceil(255/(4−1)))85 = ceil(255 / (4-1))) 를 통해 도출된 값이다. 여기서 q(i,j)q(i,j) 까지는 uniform quantization 결과물과 별반 다를 것이 없다. 하지만 우리는 dithering 을 하고 있지 않은가.
final output dithering image qfinal\ output\ dithering\ image\ q
if x(i,j)−85q(i,j)<d(i,j), p(i,j)=q(i,j)+1if\ x(i,j)-85q(i,j) < d(i,j),\ p(i,j) = q(i,j)+1
else p(i,j)=q(i,j)else\ p(i,j) = q(i,j)
왜 이게 가능할까지 아래 예시 이미지 x(i,j) 를 통해 해 보도록 하자.
n-output grayscale dithering 으로 일반화해 보자.
s=ceil(255/(n−1))s=ceil(255/(n-1))
q(i,j)=floor(x(i,j)/s)q(i,j) = floor(x(i,j)/s)
final output dithering image qfinal\ output\ dithering\ image\ q
if x(i,j)−q(i,j)s<d(i,j), p(i,j)=q(i,j)+1if\ x(i,j)-q(i,j)s < d(i,j),\ p(i,j) = q(i,j)+1
else p(i,j)=q(i,j)else\ p(i,j) = q(i,j)
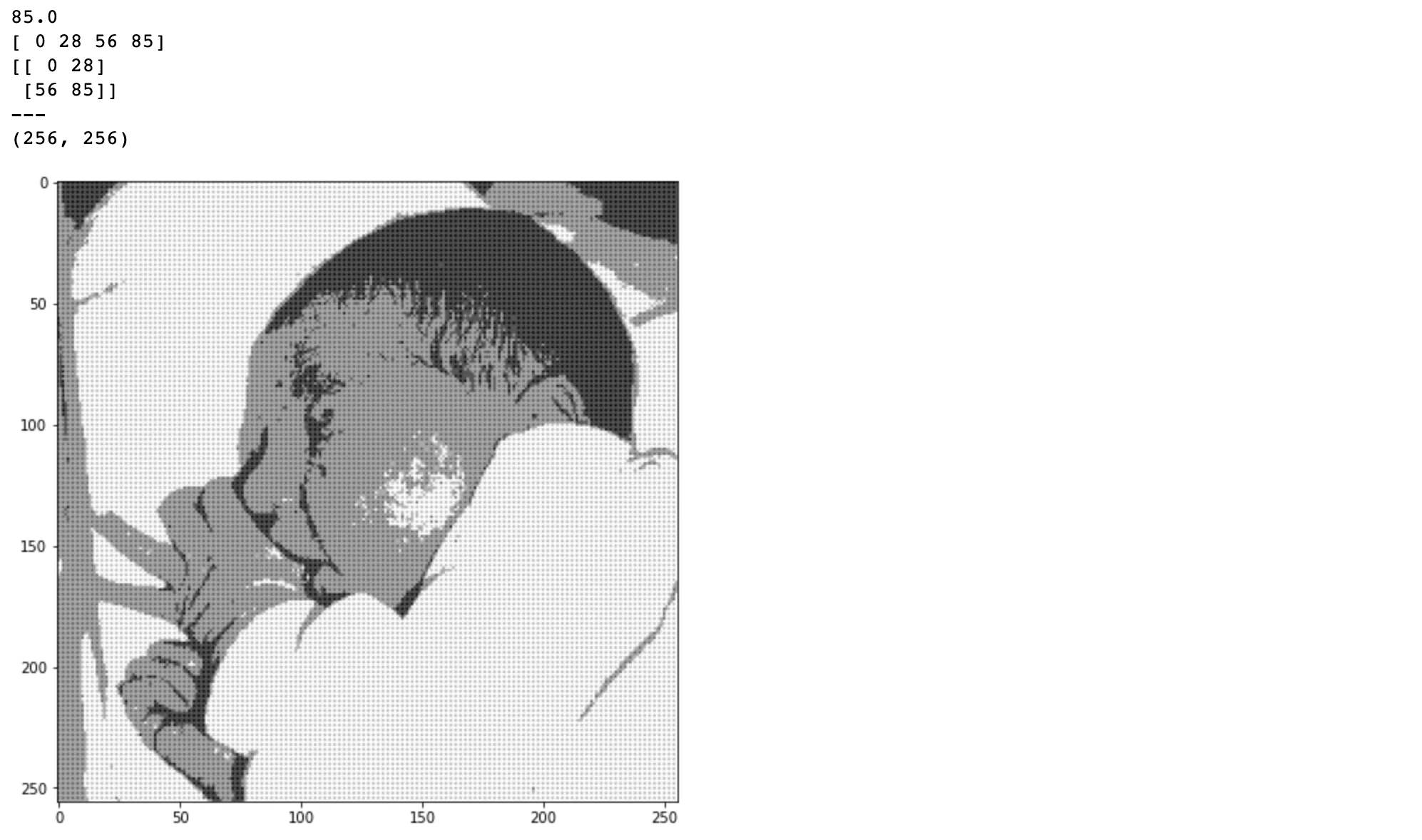
# 4-scale dithering n = 4 s = np.ceil(uint8_max / (n-1)) print(s) dithering_4 = np.linspace(uint8_min, s, n).astype(np.uint8) print(dithering_4) dithering_4_mat = dithering_4.reshape([np.sqrt(n).astype(np.uint8), np.sqrt(n).astype(np.uint8)]) print(dithering_4_mat) print('---') dithering_4_mat = np.tile(dithering_4_mat, [h//np.sqrt(n).astype(np.uint8), w//np.sqrt(n).astype(np.uint8)]) print(dithering_4_mat.shape) dithering_4_im = np.floor(im / s) + (im > im - s * dithering_4_mat) plt.figure(131, figsize = [13, 8]) plt.imshow(dithering_4_im, cmap='gray') plt.show()
Python
복사