Search
⛳

cognet.1.4.1_2. title: ‣

🚀 prev note
♻️ prev note
♻️ next note
17 more properties
논하는 세부 주제들 개요 MAX 25 links
•
전체 날짜 보기
1.
OCR 문제의 metric 에 대해 커다란 오해를 하고 있었습니다.
•
gt (groundtruth) 데이터셋은 nn 개의 이미지 각각에 대해 mm 개씩 정답값을 가지고 있고, pred (prediction) 데이터셋은 nn 개의 이미지 각각에 대해 ll 개씩 예측값을 내놓고 있습니다. 그런데 이때 단일 이미지에서 gt 와 pred 는 1:1 대응이 아니기 때문에 처음에 제가 1:1 대응되어 데이터가 주어진다고 가정하고 작성했던 metric 소스코드를 사용할 수 없었습니다. 왜 이걸 이제 깨달았지
•
gt 가 don’t care 가 아닌 경우를 먼저 생각해 봅니다.
gt 와 pred 의 문자 영역 IoU 가 0.5 이상 일치하고 단어도 일치하는 경우를 pred 와 gt 의 ‘연결’ 이라고 표현하겠습니다. pred 와 gt 는 다대다 연결이 가능합니다.
◦
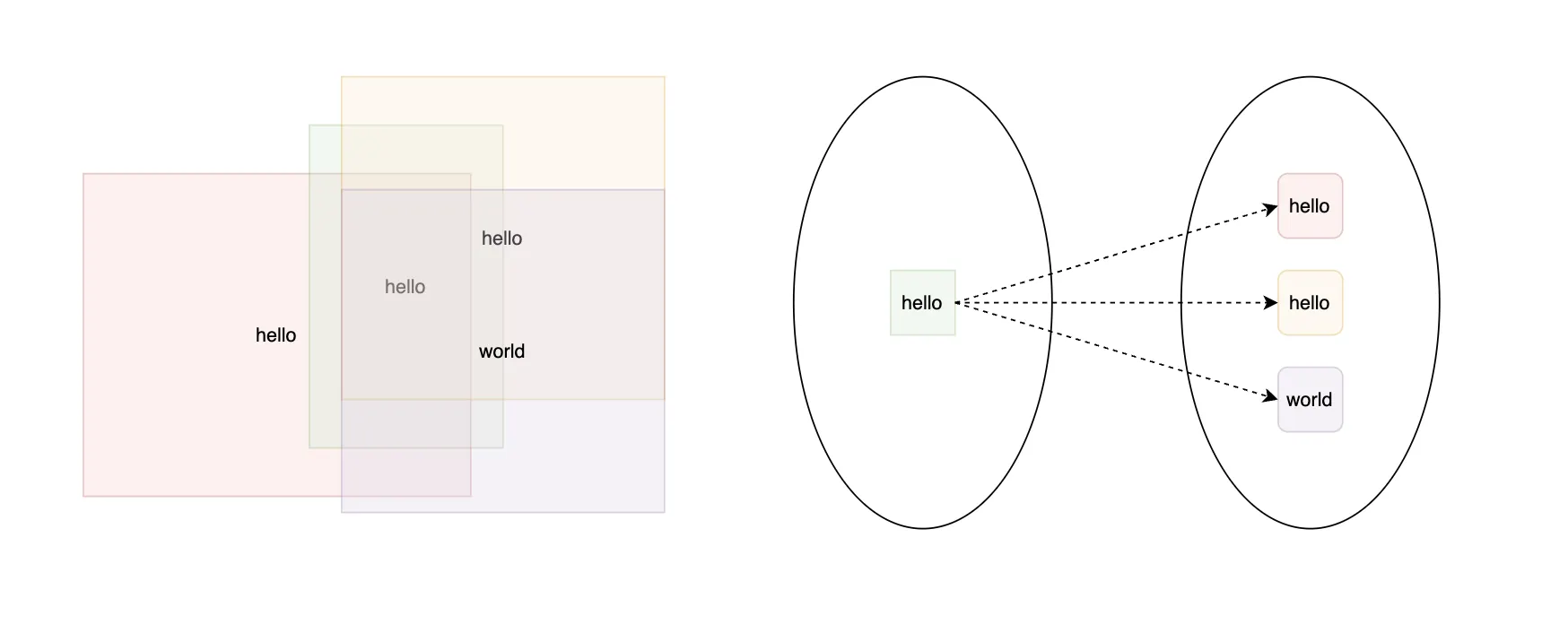
len(gts) == 1 이고 위 그림과 같은 상황에서 정의된 명세를 곧이곧대로 사용하면 metric 은 다음과 같이 산출됩니다.
▪
T′=4T'=4 (예측한 모든 set)
▪
M=1M=1 (영역도 일치하고 단어도 일치한 set = 연결 개수)
▪
G=1G = 1 (문자 영역과 단어의 gt set)
▪
이 경우에는 문제가 없다.
◦
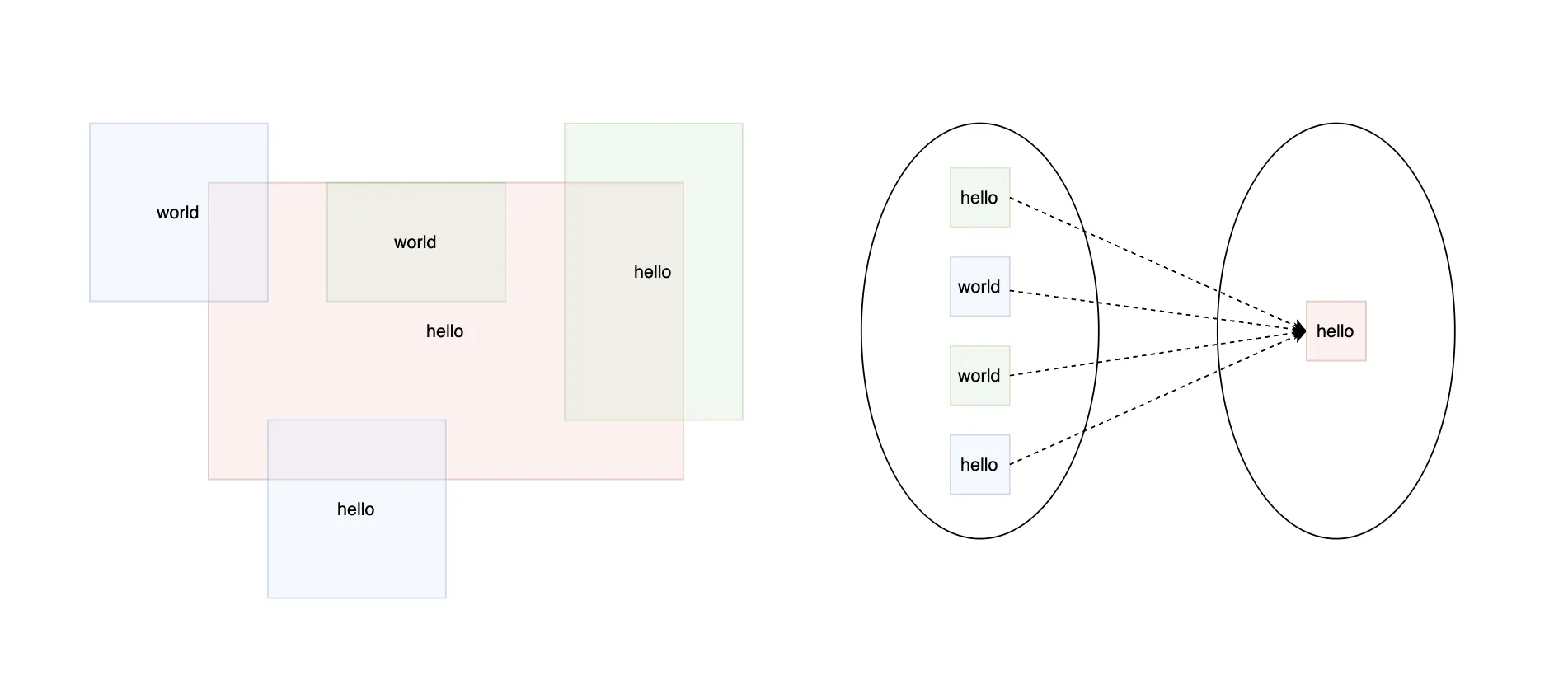
len(gts) == 1 이고 위 그림과 같은 상황에서, 하나의 gt 에 여러 pred 가 매칭되는 경우, 정의된 명세를 곧이곧대로 사용하면 metric 은 다음과 같이 산출됩니다.
▪
T′=5T'=5 (예측한 모든 set)
▪
M=2M=2 (영역도 일치하고 단어도 일치한 set = 연결 개수)
▪
G=1G = 1 (문자 영역과 단어의 gt set)
▪
이렇게 되면 갑자기 M>GM >G 가 되어 recall>1\mathrm{recall}>1 이 된다는 문제가 있습니다. 재현율(recall)은 반드시 1 이하여야 하기 때문에 생각이 필요합니다. 상식적으로 재현율은 1이 되어야 하고, 정밀도는 2/5 가 되어야 합니다. 따라서 recall\mathrm{recall} 은 한번도 연결되지 못한 gt 들을 세어 계산해야 합니다.
◦
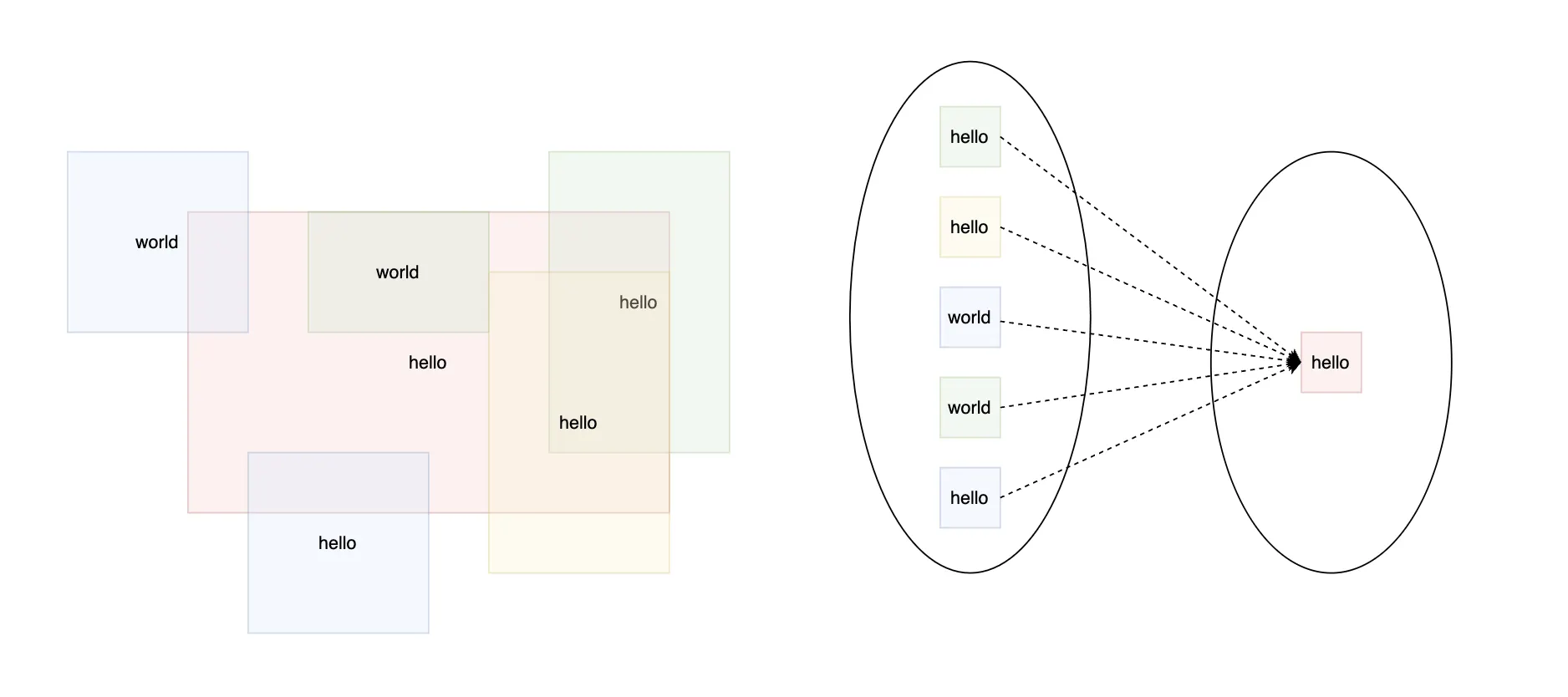
len(gts) == 3 이고 위 그림과 같은 상황에서, 하나의 pred 가 여러 gt 와 매칭되는 경우 정의된 명세를 곧이곧대로 사용하면 metric 은 다음과 같이 산출됩니다.
▪
T′=1T'=1 (예측한 모든 set)
▪
M=2M=2 (영역도 일치하고 단어도 일치한 set = 연결 개수)
▪
G=3G = 3 (문자 영역과 단어의 gt set)
▪
이렇게 되면 갑자기 M>T′M > T' 가 되어 precision>1\mathrm{precision}>1 이 됩니다. 재현율과 마찬가지로 정밀도(precision)는 반드시 1 이하여야만 합니다. 상식적으로 재현율은 1/3 이 되어야 하고, 정밀도는 1 이 되어야 합니다. 따라서 precision\mathrm{precision} 은 한번도 연결되지 못한 pred 들을 세어 계산해야 합니다.
class Approach(abc.ABC): def __init__(self, ...): # ... self.matrix = matrix.Matrix() self.matrix.n_words_gt = len(gts) self.matrix.n_words_pred = len(preds) # ... def cal_matrix(self): for gt, pred in self.yield_pair(): if self.matrix.is_end2end_tp(gt, pred, check_iou=False): gt.is_connected = True pred.is_connected = True self.matrix.update(self.preds, self.gts) class Matrix(): def update(self, preds, gts): # preds, gts are list or LinkedList for pred in preds: if pred.is_connected: self.n_words_matched_pred += 1 for gt in gts: if gt.is_connected: self.n_words_matched_gt += 1 @property def precision(self): if self.n_words_pred == 0: return 0 return self.n_words_matched_pred / self.n_words_pred @property def recall(self): if self.n_words_gt == 0: return 0 return self.n_words_matched_gt / self.n_words_gt
Python
복사
•
gt 가 don’t care 인 경우는 간단합니다. 그냥 이미 연결이 되어 있다고 쳐 버리면 끝납니다.
class Node(): def __init__(self, ... ): # ... self.is_connected = False if self.sentence == DONT_CARE: self.is_connected = True # ...
Python
복사
2.
sorting 과 multiprocessing 을 제외한 polygon 연산부분을 직접 구현하고, numba 로 최적화하여 벤치마킹했습니다. O(n2)\mathrm{O(n^2)} 순수 python 알고리즘 대비 최종 결과물은 대략 약 50배~100배 정도의 성능 향상이 있었습니다.
it/s 는 1초당 image 1장에 해당하는 preds 와 gts 를 처리할 수 있는 양에 해당합니다.
•
10 images, 10000 preds (1000 preds/image), 202 gts
◦
약 50배 성능 향상
single core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
0.21it/s
-
1.46it/s
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
0.27it/s
-
2.56it/s
multi(10) core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
1.54it/s
-
7.96it/s
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
1.99it/s
-
10.39it/s
•
50 images, 50,000 preds (1000 preds/image), 3139 gts
◦
약 90배 성능 향상 (괄호는 프로그램이 종료하는 사건까지 걸린 시간)
single core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
0.11it/s (7:16)
0.21it/s (3:56)
1.44it/s (0:34)
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
0.14it/s (5:54)
2.56it/s (3:14)
1.32it/s (0:37)
multi(10) core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
1.45it/s (0:34)
2.05it/s (0:24)
8.56it/s (0:05)
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
1.86it/s (0:26)
2.62it/s (00:19)
9.82it/s (0:05)
•
50 images, 500,000 preds (10,000 preds/image), 3271 gts
multi(10) core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
-
-
0.86s/it (0:57)
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
-
-
1.02it/s (0:48)
•
50 images, 5,000,000 preds (100,000 preds/image), 3271 gts
multi(10) core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
-
-
11.82s/it (9:51)
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
-
-
10.28s/it (8:34)
◦
O(nlog(n))\mathrm{O(nlog(n))} 과 O(n2)\mathrm{O(n^2)} 의 실행시간에 큰 차이가 나지 않는 이유는, naive 접근과 sort 접근은 모두 bbox 를 통해 ‘계산할 가치가 있는 다각형’ 을 필터링해내는 방식으로 작동하는데 이때 필터링되는 bbox 의 개수는 비슷하기 때문임. sorting 과 filtering (시간복잡도에 영향을 받음) 에 걸리는 시간보다 matching 에서 소비되는 시간이 훨씬 길기 때문일 것이라고 추측.
•
10892 images, 10,892,000 preds (1000 preds/image), 785,498 gts
◦
돌릴 엄두가 안난다.
single core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
multi(10) core
native python
polygon lib
numba optimized
alg: naive O(n2)\mathrm{O(n^2)}
13.49it/s (13:27)
alg: sort O(nlog(n))\mathrm{O(nlog(n))}
15.62it/s (11:37)