영상처리 연산
영상의 화소(pixel)값을 변경하는 일을 영상처리 연산이라고 한다.
•
화소 단위 처리: 하나의 화소값만을 사용하여 화소값을 변경
•
영역 단위 처리: 이웃 화소들을 참조하여 화소값을 변경
•
영상 단위 처리: 기하적 변환(Transform)
영상 단위 처리
보간 (interpolation)
주위의 값을 근거로 함수값을 추정하는 것을 보간 (interpolation) 이라고 한다.
보간에는 다음과 같은 것들이 있다.
•
최근접 보간 (nearest-neighbor interpolation)
•
선형 보간 (linear interpolation) (2차원에서는 양선형 보간 : bilinear interpolation)
•
3차 곡선 보간 (cubic interpolation) (3차원에서는 양방향 3차곡선 보간 : bicubic interpolation)
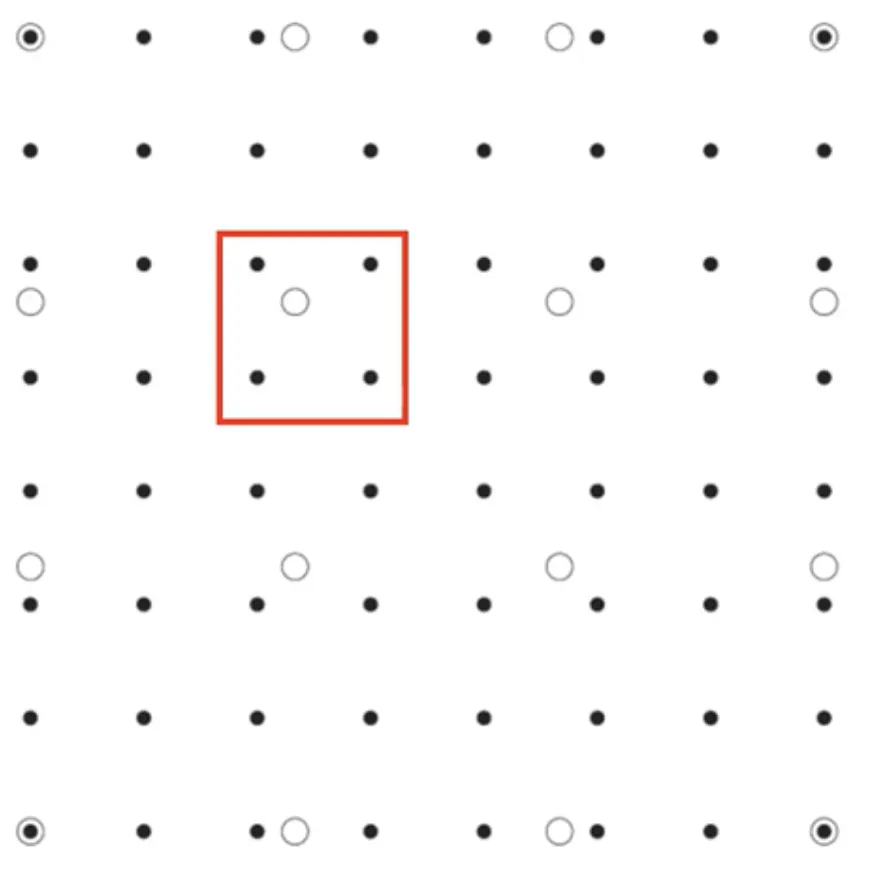
위 그림에서 흰 동그라미는 원래의 영상 (4x4) 이고, 검은 동그라미는 보간을 통해 만들어내고자 하는 영상 (8x8) 인 경우이다.
우리가 관심가지고 보간을 하는 스코프는, 위 그림과 같다.
아래 그림에서는 반대로 흰 동그라미는 보간을 통해 만들어내고자 하는 영상 (4x4) 이고, 검은 동그라미는 우리가 가지고 있는 영상 (8x8) 으로, 8x8 영상을 4x4 영상으로 축소하는 경우를 의미하지만, 딱히 달라지는 것은 없다.
최근접 보간 (nearest-neighbor interpolation) 은 보간값으로 가장 가까운 값을 취하는 방법이다.
선형 보간 (linear interpolation) 은 원래 함수 값들을 직선으로 연결하고, 그 직선 위의 값을 보간값으로 선택하는 방법이다.
꽤 단순해 보이지만, 만약 선형보간이 2차원으로 확장되었을 때는 조금 더 생각을 해 보아야 한다.
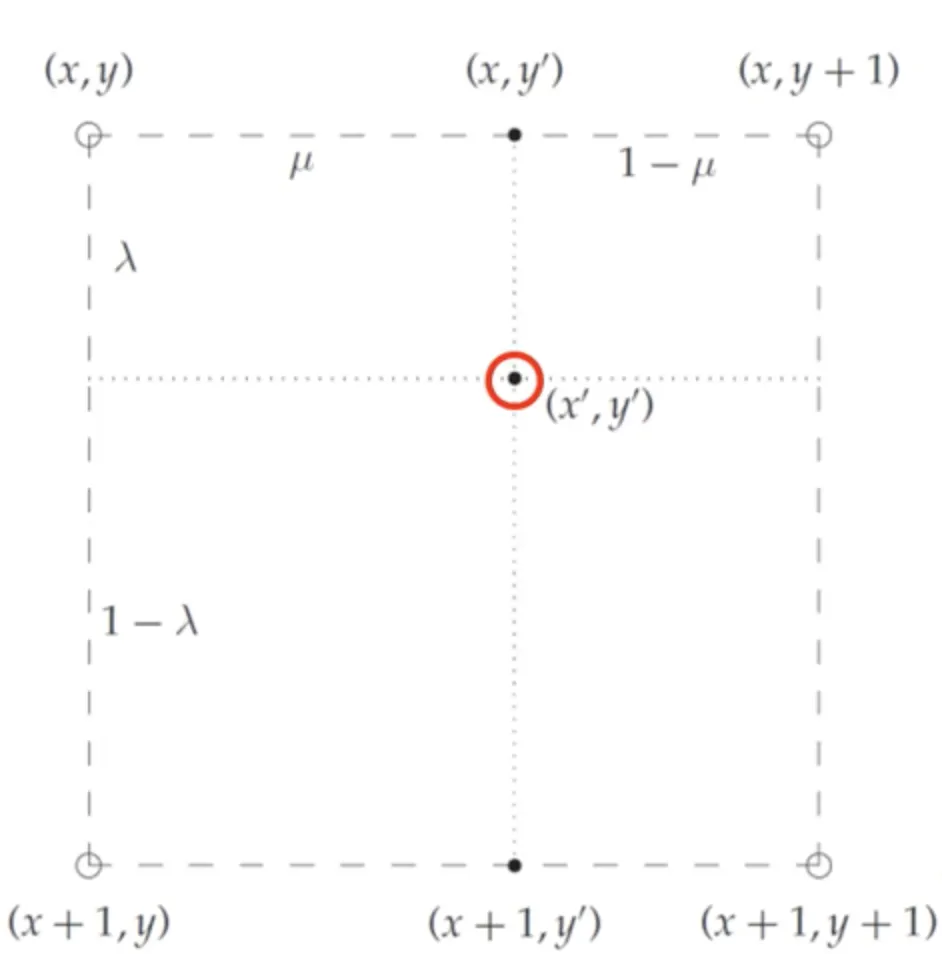
최종적인 목표는 의 함수값을 찾아내는 것이다.
먼저 가로방향 선형보간을 거친다.
가로방향 선형보간을 거쳐 얻은 을 바탕으로 세로방향 보간을 통해 최종값을 만든다.
아래 그림들은 각각 원본 이미지, nearest neighbor 과 bilinear 을 통해 보간한 결과물이다.
양선형 보간을 하면 영상이 주변 픽셀들의 가중 평균값으로 채워지기 때문에 부드럽지만 흐려진다.
최근접 보간과 선형보간의 일반화 (보간함수를 활용한 표현)
최근접 보간과 선형보간 (양선형 보간) 은 일반적인 보간의 두 가지 특수한 경우이다.
수식 설명 : 이기 때문에, 의 정의역은 함수 R 의 (-1, 0) 범위에서 움직이고, 의 정의역은 함수 R 의 (0, 1) 범위에서 움직인다.
따라서 최근접 보간과 선형보간은 에 대하여 선대칭일 것이다.
최근접 보간 (nearest neighbor) 에 사용되는 보간 함수 R
선형 보간 (linear) 에 사용되는 보간 함수 R
3차 곡선 보간
3차 곡선 보간 (cubic interpolation) 은 2개의 값이 아닌, 4개의 값을 사용하여 보간을 수행한다.
3차 곡선 보간의 보간 함수는 다음과 같다.
1차원에서의 선형보간이 2차원에서 양선형 보간이 되었듯, 1차원에서 3차 곡선 보간은 2차원에서 양방향 3차곡선 보간이 된다.
•
1차원 : 선형 보간 (linear interpolation)
•
2차원 : 양선형 보간 (bilinear interpolation)
•
1차원 : 2개의 값
•
2차원 : 4개의 값
.
•
1차원 : 3차곡선 보간 (cubic interpolation)
•
2차원 : 양방향 3차곡선 보간 (bicubic interpolation)
•
1차원 : 4개의 값
•
2차원 : 16개의 값
nearest / bilinear / bicubic
아무래도 조금 더 많은 정보를 바탕으로 interpolation 을 수행했기 때문에 결과가 더 좋을 가능성이 높다.
회전 (Rotation)
어떤 점을 반시계 방향으로 theta 만큼 회전해서 다른 점으로 mapping 하는 행렬은 다음과 같다.
이때, 행렬 R 은 orthonormal 하기 때문에, 행렬 R 의 역행렬 (Inverse)과 전치행렬 (Transpose) 은 동일하다.
어떤 영상을 회전시킨다는 것은 다음과 같다. 검정색이 원본 영상을 의미하고, 흰색 점은 원본 영상을 반시계 방향으로 theta 만큼 회전시킨 영상을 의미한다.
영상은 항상 upright 하기 때문에 (수직으로 바로세워져 있어야 하기 때문에), 회전된 영상을 둘러싼 사각형이 회전된 영상의 크기가 된다.
위 성질을 잘 생각해야 한다. 원본 영상보다 크기가 커진다는 성질을 잘 생각하라는 말이다. 그럼 이제 거꾸로 생각하자. 회전된 영상 중, 아래의 조건을 만족하는 위치만, 원본 영상 내에 존재하는 것이다. 다시 말하면, 회전된 영상은 원래 영상에 없는 부분의 정보까지 가지고 있지 못한데, 이를 찾아내는 과정은 다음과 같다.
1.
회전된 영상의 모든 영역(a) 에 대해서, (a)의 모든 점들이 회전 전의 어떤 위치(b) 에 있는지 먼저 찾아내고
2.
회전 전의 위치(b) 가 원본 영상 영역 내에 존재하는지(c) 확인하고
3.
해당 픽셀의 위치(b) 가 원본 영상 내에 존재한다면 (c) 은 밝기값을 가지고
4.
해당 픽셀의 위치(b) 가 원본 영상 내에 존재하지 않는 영역(d) 에 해당한다면 값을 채우지 않는다.
위 과정 (1~4) 에서 2 를 잘 생각해 보자. 회전 전의 위치를 찾았을 때, 그 위치 (b) 가 원본 영상의 각 픽셀에 (가령, 정수 index 로) 딱 떨어지지 않을 수 있다. 아래 그림과 같은 상황을 의미한다.
이럴 때, 적절한 밝기값을 찾아내기 위해 위에서 배운 보간을 사용한다.
rotation 을 활용하는 다양한 자료들을 보다 보면... rotation 이야기를 하는데 계속 보간 이야기가 나왔고, 이것이 도대체 이런 이야기가 왜 나왔을까 고민을 해 보았을 때 느낌은 알았지만 그 이유를 정확히 이해하지는 못했다. 이제 보간이 어느 부분에서 사용되는지 알겠다.
opencv python api 에서는 다음과 같은 방법으로 rotation 을 수행한다.
1.
rotation matrix 얻기 (cv2.getRotationMatrix2D())
2.
rotation matrix 를 통해 Affine 변환 (cv2.warpAffine())
그냥 회전을 시키는 경우
from scratch 로 작성해 보자.
TODO : 소스코드 실습
야발 내가 이걸 왜 짜겠다고 나서서... 짜는중...
low_left = np.matmul(R, np.array([0, im.shape[0]-1]))
low_right = np.matmul(R, np.array([im.shape[1]-1, im.shape[0]-1]))
top_left = np.matmul(R, np.array([0, 0]))
top_right = np.matmul(R, np.array([im.shape[1]-1, 0]))
print('\n---\n{}\n{}\n{}\n{}'.format(low_left, low_right, top_left, top_right))
x_min = np.min([low_left[0], low_right[0], top_left[0], top_right[0]])
y_min = np.min([low_left[1], low_right[1], top_left[1], top_right[1]])
x_max = np.max([low_left[0], low_right[0], top_left[0], top_right[0]])
y_max = np.max([low_left[1], low_right[1], top_left[1], top_right[1]])
print('\n---\n{}\n{}\n{}\n{}'.format(x_min, y_min, x_max, y_max))
# x_range, y_range, ... -> rotated
x_range = np.arange(np.floor(x_min), np.ceil(x_max))
y_range = np.arange(np.floor(y_min), np.ceil(y_max))
x_range_tile = np.repeat([x_range], len(y_range), axis=0)
y_range_tile = np.repeat([y_range], len(x_range), axis=0).T
print('\n---\n', 'shape:', x_range_tile.shape, y_range_tile.shape)
x_y_index = np.concatenate([[x_range_tile], [y_range_tile]], axis=0).reshape(-1, 2)
print('\n---\n', x_y_index)
print('shape :', x_y_index.shape)
for i in range(len(x_y_index)):
res = np.matmul(R.T, x_y_index[i])
if (np.array([0, 0]) < res).any() & (res < im.shape).any():
interpolation(res)
# res <- interpolation(res)
else:
0
Python
복사
x_y_index