Search
🔵

bdf_3. title: 확률변수와 구체적인 사건의 표기법을 정확히 익혀두지 않으면 디퓨전모델의 수학적 표현을 이해하기 어렵다.

생성
🚀 prev note
🚀 next note
♻️ next note
14 more properties
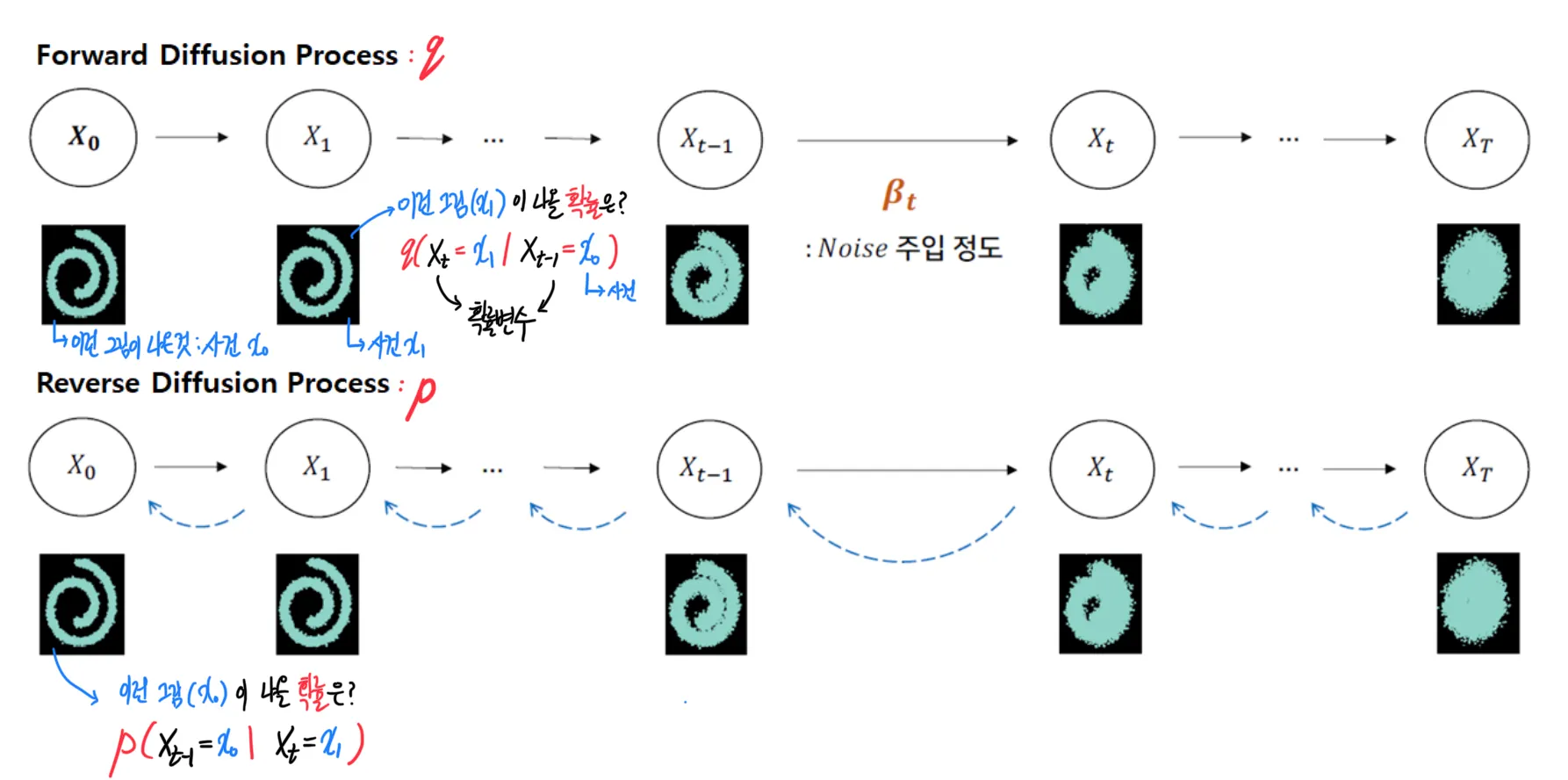
디퓨전모델에서 pp 는 노이즈를 제거하는 reverse process를 의미하고, qq 는 노이즈를 추가하는 forward process 를 의미한다. 이건 이미 수많은 블로그들에서 설명하고 있다. 그런데 pp 나 qq 는 함수일까 확률분포일까? 어떨 때는 함수처럼 작동하는 듯 하고, 어떨 때는 분포 표현처럼 작동하기도 한다. pp 나 qq 는 확률함수가 아니라 확률분포다. 이를 헷갈리면 절대 이해할수가 없다.
표현
동치 표현
값
해석
pθ(Xt∣Xt+1)p_{\theta}(X_t|X_{t+1})
확률분포
Xt∣Xt+1X_t|X_{t+1} 는 ‘Xt+1X_{t+1} 이라는 사건이 발생했을 때, XtX_t 라는 사건이 발생한 사건’ 을 의미한다. Xt∣Xt+1X_t|X_{t+1} 자체도 하나의 확률변수로 해석 가능하다. 그렇다면 Xt∣Xt+1X_t|X_{t+1} 은 하나의 확률로 확정할 수 없다. Xt∣Xt+1X_t|X_{t+1} 사건이 발생할 확률은 분포 형태로 나타날 것이다.
pθ(xt∣xt+1)p_{\theta}(x_t|x_{t+1})
pθ(Xt=xt∣Xt+1=xt+1)p_{\theta}(X_t=x_t|X_{t+1}=x_{t+1})
확률
사건 Xt+1X_{t+1} 이 정확히 xt+1x_{t+1} 일 때, 사건 XtX_{t} 이 정확히 xtx_{t} 일 때의 확률을 의미한다.
pθ(x0)p_{\theta}(\mathrm{x_0})
pθ(X=x0)p_{\theta}(X=\mathrm{x_0})
확률
통상적으로 확률변수는 기울임 대문자 XtX_{t} 로 표현하고, 구체적인 값은 소문자로 표현한다. 통상적으로 벡터는 굵은 정자체를 사용한다. x0\mathrm{x}_0 은 벡터를 의미한다. 여기서 벡터는 벡터가 될 수 있는 모든 것이다. 이미지도 flatten 하면 벡터가 될 수 있다.
pθ(x0∣x1)p_{\theta}(\mathrm{x}_0|\mathrm{x}_{1})
pθ(Xt=x0∣Xt+1=x1)p_{\theta}(X_t=\mathrm{x}_0|X_{t+1}=\mathrm{x}_1)
확률
사건 Xt+1X_{t+1} 이 정확히 x1\mathrm{x}_1 일 때, 사건 XtX_{t} 이 정확히 x0\mathrm{x}_0 일 때의 확률을 의미한다.
블로그들에서 한번쯤 찾아볼 수 있는 그림이다(출처). 각각의 과정을 확률 표현식으로 정확히 서술할 수 있어야 한다.
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료을 보관해 두는 영역입니다.
1.
None
from : 과거의 어떤 원자적 생각이 이 생각을 만들었는지 연결하고 설명합니다.
1.
•
비단 디퓨전모델뿐 아니라 확률과 관련된 모든 표현에 적용되는 내용이다.
2.
•
추상적으로 이해한 뒤, 수식적으로 이해하려고 하는데 노테이션이 정립되지 않아 이해에 지나치게 많은 시간이 소비되었다. pp 와 qq 를 ‘확률함수’ 라고 생각했기 때문이다. 그것을 전제로 모든 생각을 펼쳐 나가다 보니 계속 논리가 맞지 않았다.
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는지 연결합니다.
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는지 연결합니다.
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되거나 이어지는지를 작성하는 영역입니다.
1.
None
ref : 생각에 참고한 자료입니다.
1.
None