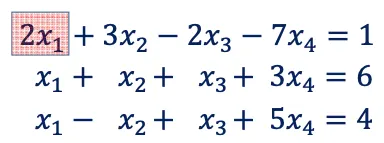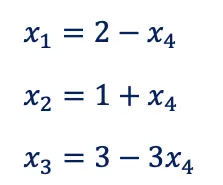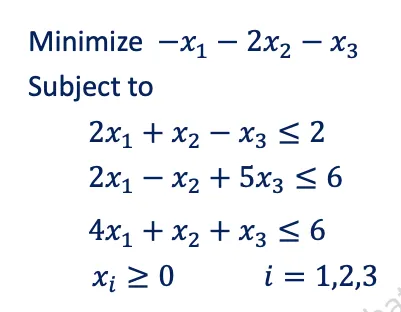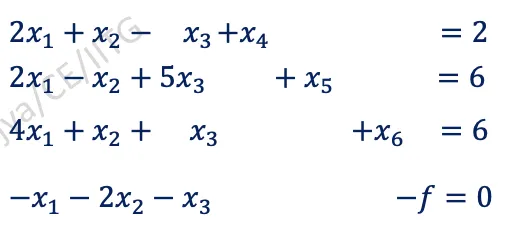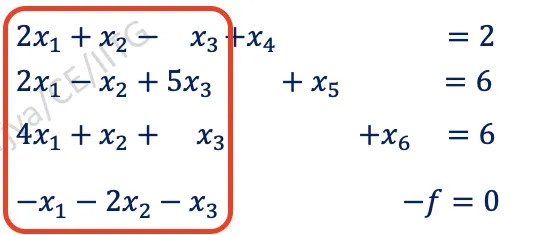A basic solution is one in which {(n-m variable) are set equal to zero and solution can be obtained for the m number variable} ... 문장이 어려운데, basic solution 은, n-m 개의 변수가 "0이라고 설정" 하고, m 개의 변수들에 의해 등식을 만족시키는 다양한 상황들 중 하나(one in which) 이다. The solution obtain by setting independent variable equal to zero is called basic solution. (이것을 보아, 위에서 말했던 "0이라고 쳐보는" n-m 개의 변수들이 독립변수를 의미하는 듯하다.) 아래 예시* 를 보자.

출처

수집시간

2021/08/10 14:38

연결완료

1 more property

pivot = x1

이 상황에서는 종속변수가 x1, x2, x3, 독립변수가 x4 이므로 x4 = 0 이 basic solution 이다.

x1, x2, x3 를 독립변수로 보면 안되는건가? 그럼 x4 (종속변수) 이 졸졸졸 끌려오잖아 헤헤

하지만 꼭 pivot 을 무엇으로 잡을 필요는 없다.

당연히 처음에는 x1, x2, x3, x4 사이에는 어떠한 위계도 존재하지 않는다. 따라서 어떤 녀석을 pivot 으로 잡느냐에 따라 basic solution 은 정말 다양하게 나타날 수 있다.

자 그럼 여기서 이런 생각을 할 수 있다. basis (기저) is The collection of variables not set equal to zero to obtain the basic solution* is called the basis. 각 상황마다 기저가 다르게 된다.

변수의 개수를 n 개, 주어진 등식 (조건이 아니다! 부등식인 순간 변수가 늘어나게 된다!) 의 수를 m 개라고 했을 때 nCm 개의 basic solution 이 나올 수 있게 된다.

이렇게 n변수 방정식을 풀어내는 상황을 잘 일반화해 보면 방정식 앞부분에는 저렇게 잘 소거되는 변수들이 있을것이고 뒷쪽에는 변수들이 다 살아있을텐데 이것을 Pivotal, non pivotal 이라고 부르는 것 같다. 여기서 잘 보면 변수가 n 개이고 식이 m 개이다.

이거 별도 문서로 만들것

예제

decision variable : x1, x2, x3 objective function : 2x1 + x2 + x3 constraints : x1+x2 ≤ 1, x1 - x3 ≥ 2 , x1+x2+x3 = 5, x1 ≥ 10, x2 < 0 feasible solution : 모든 제약조건 (all constraints) 을 충족하는 그 무엇이든지 만족하는 (x1, x2, x3) optimal solution : feasable solution 인데, objective function 이 최대이거나 최소이거나 한 것 에 따라, 다음과 같이 전개된다.

•

objective : f=−x1−2x2−x3f = -x_1 - 2x_2-x_3f=−x1​−2x2​−x3​

•

subject to : constraints

Linear programming 에는 세 가지 특성이 있다. (1) 모든 objective function 은 minimization type 이다. (최대화여도 최소화로 돌려풀 수 있음)* (2) 모든 제악조건 (constraints) 는 surplus variable, slack variable을 활용해서 등식으로 표현**할 수 있다. (3) 모든 decision variable 은 양수이다.*** (음수이더라도 두 양수의 차로 바꾸어 생각할 수 있음.) 의 (2) 에 따라 다음과 같이 전개된다.

A basic solution is one in which {(n-m variable) are set equal to zero and solution can be obtained for the m number variable} ... 문장이 어려운데, basic solution 은, n-m 개의 변수가 "0이라고 설정" 하고, m 개의 변수들에 의해 등식을 만족시키는 다양한 상황들 중 하나(one in which) 이다. The solution obtain by setting independent variable equal to zero is called basic solution. (이것을 보아, 위에서 말했던 "0이라고 쳐보는" n-m 개의 변수들이 독립변수를 의미하는 듯하다.) 아래 예시* 를 보자. 에 따라, 다음과 같이 분리 가능하다. 붉은 영역은 pivotal variables, 나머지 영역은 non pivotal variables 이다.

근데 이게 진짜 어이없게 pivot 을 잘못 잡고 소거하면, 잘못된 결론에 도달하게 될 수 있다. 그 이유는 우리의 전제가 x1~x6 이 모두 양수여야 한다는 것이다. 그런데 도대체 왜 pivot 을 하나 잘못잡았다고 아예 다른 값들이 나와버리면 되겠나...? 계산을 잘못한건가...?

물론 이런 문제가 발생하는 이유는, 피벗을 잘못 잡고 계산을 잘못한 게 아니라, 부등식을 등식으로 바꾸면서 x4, x5, x6 을 추가했고, 이것과 동시에 x4, x5, x6 이 양수여야만 한다는 조건을 추가했다. 와 이걸 왜 생각을 못했지 그 조건이 pivot 을 통해 연산하는 과정 속에 녹아있지 않기 때문에 마지막에 숫자가 나온것을 보고 나서야 아, 이거 infeasible 하네! 라고 사람이 인지할 수 있게 되는 것이다.

여튼, pivot 을 잘못 잡으면, 마지막에 이게 유효한지 아닌지 확인을 하게 되어 비효율적이다. 이것을 어떻게 더 잘 할 수 있을까? 어떻게 더 효율적으로 pivot 을 잡고 연산해서 해를 구할 수 있을까? 를 고민하면서 나온 것이 Now what is the rule, how to select the pivoting element? Select the minimum one to avoid infeasible solution Thus the general rule is "Select the minimum one to avoid infeasible solution" ... SIMPLEX METHOD 인 것 같다. 이에 대해서는 추가적인 공부가 필요하다.

이를 구하는 과정과 관련해서