•
수습기간 3개월간 팀마다 3주씩 돌기로 했었다. 원래는 기획팀을 가보기로 했었는데 회사사정상 Ai solution lab 으로 바로 가게 되었다. 도 태스크를 주셨다.
◦
배경지식
•
OCR 태스크는 논리적으로 두 개의 단계로 구성된다. Deep Learning based OCR 은 (첫 번째 단계) 문자영역을 찾아내는 detection 모델과 (두 번째 단계) 문자를 식별하는 recognition 모델로 이루어져 있다.
•
해야 하는 일은 End2End F1 Score 을 산출하는 것이다. 으로부터 이 과제를 부여받은 것은 @9/15/2022쯤이었지만, @10/26/2022쯤 뒤늦게 알게 된 사실은 MMOCR 등의 OCR 프레임워크들조차 Detection F1 Score 이나 Recognition Word Accuracy, Recognition Character F1 Score 등을 계산해 주는데 비해 Detection + Recognition = End2End F1 Score 을 계산해주지는 않는다. 따라서 MMOCR 등 프레임워크를 사용하더라도 모델 출력값을 받아서 이 기능을 직접 구현해야만 한다. 따라서 이 에셋은 AiHub OCR 국가지원사업은 물론 다른 OCR 태스크에도 유용하게 사용될 수 있다.
◦
End2End F1 Score 의 정의는 아래 과제문서를 참고하라.
◦
•
이때 최적화가 굉장히 중요하게 작용한다. 보통 시간복잡도가 이기 때문이다. 컴파일 언어 사용을 권장한다. Distribution or Multiprocess 를 사용하라.
•
모든 Object detection task 가 그러하듯, prediction 과 ground truth 는 1:1 대응이 되지 않는다. prediction 순서와 ground truth 의 순서 및 개수는 보장되지 않는다. 보통 prediction bbox 이 ground truth 보다 훨씬 많을 것이다.
•
대표적인 OCR 대회는 ICDAR 이고, ICDAR 만의 Label 포맷이 있다.
{x1},{y1},{x2},{y2},{x3},{y3},{x4},{y4},{label}
{x1},{y1},{x2},{y2},{x3},{y3},{x4},{y4},{label}
{x1},{y1},{x2},{y2},{x3},{y3},{x4},{y4},{label}
Plain Text
복사
ICDAR format. 이미지파일 1개당 위와 같은 텍스트파일 1개가 제공된다.
일반적인 object detection task bounding box label 과 다르게, 그 형식이 left_top, right_bottom 형태가 아님을 알 수 있다. OCR 문제에서는 문자가 존재하는 영역 사각형이 이미지의 변에 평행하거나 수직인 직사각형 형태일 것이라는 점을 보장할 수 없기 때문이다. 텍스트에 주어진 text detection 형식은 polygon 이다.
•
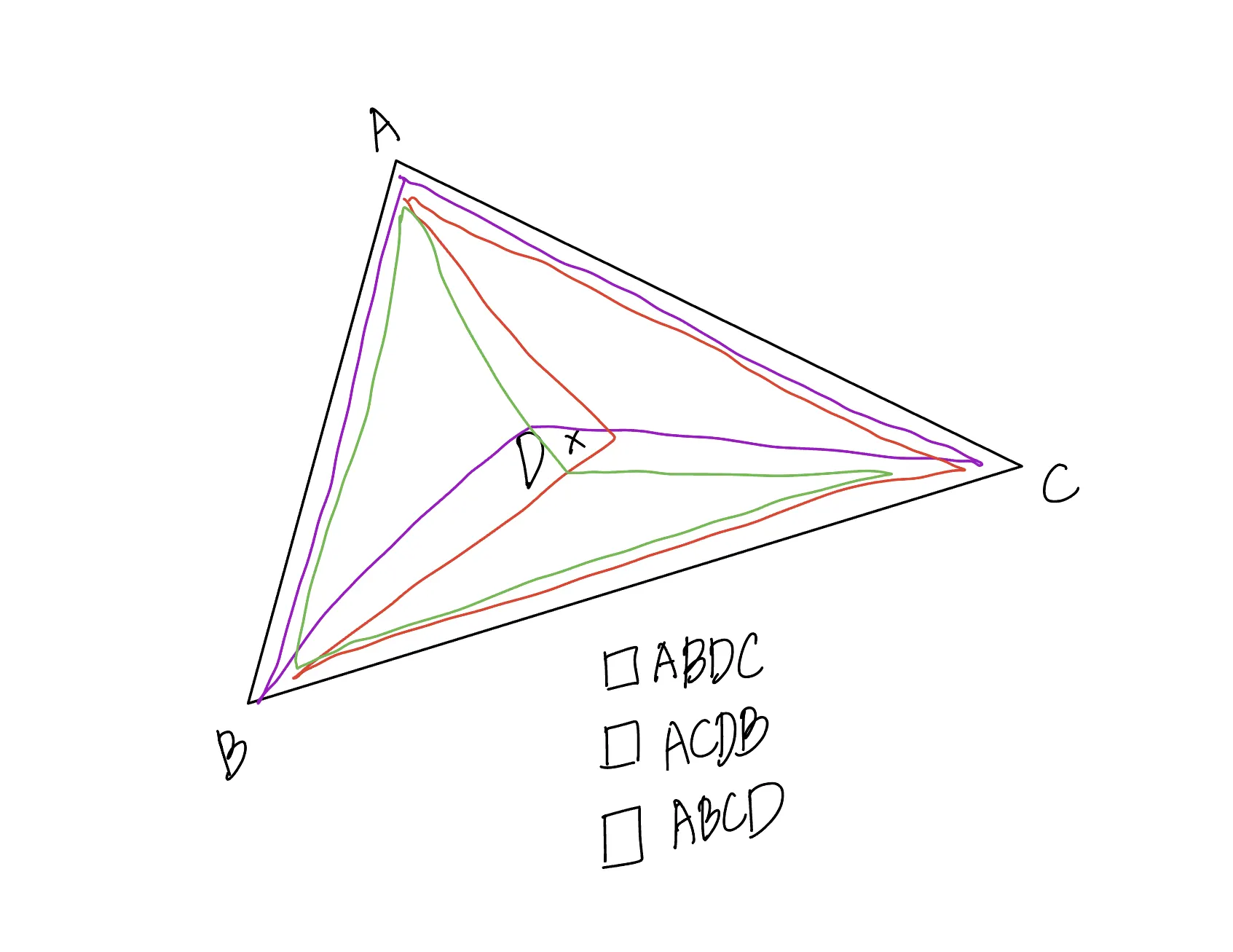
만약 주어진 네 좌표에서, 임의의 세 개의 좌표로 만드는 삼각형이 나머지 한 개의 좌표를 포함한다면, 네 개의 좌표로 만들 수 있는 사각형은 유일하지 않다.
•
따라서 반드시 주어지는 는 ‘linear ring’ 을 만들 수 있는 형태로 공급된다.
•
레이블러의 실수에 대해 강인하게 설계되어야 한다. 가령 GT 데이터의 labels key 가 비어 있는 레코드들을 don’t care 이라고 보는 것이 합리적이지만, iscrowd == False 인데도 labels key 가 비어있는 레코드가 발견될 수 있다. 혹은 주어지는 가 ‘linear ring’ 형태로 들어오지 않는 경우가 존재할 수 있으므로 처리를 거부하는 예외처리 로직이 있으면 좋을 것이라고 한다. 에 따르면, 이러한 상황들은 그냥 레이블러의 실수이기 때문에 전처리 과정에서 그냥 버리면 된다고 하셨다.
•
텍스트 영역에 가림(occlusion)이 있는 경우 하나의 검출 대상에 대해서도 여러 polygon 으로 구성되어 있을지 모른다.
•
을 계산할 때, 문장 내 단어가 1개로 구성되어 있다면, 해당 단어를 구성하는 문자 n 개 중 1 개라도 틀리면 그냥 score 을 0 으로 계산하는 것이 맞다.
생각하기
•
최적화의 원칙
1.
Single instruction 실행 시간을 단축하는 미시적인 최적화보다 알고리즘 시간복잡도 단축과 같이 거시적인 최적화가 선행되어야 할 뿐 아니라 훨씬 중요하다.
2.
무엇이 더 시간을 많이 잡아먹는지 알기 위해서는 요소별 소요시간을 정확히 측정하고, 자주 일어나는 연산을 빠르게 한다 (Common Case Fast).
•
벤치마크 데이터를 적절히 사용하라.
3.
병렬적으로 처리하라 (Performance via parallelism).
•
더 나은 코드를 작성하는 습관
1.
2.
다양한 알고리즘이 나타날 수 있으므로 알고리즘을 커스텀으로 쉽게 추가할 수 있도록 설계
3.
다양한 백엔드와 다양한 라이브러리를 바꿔가며 실행해볼 수 있도록 래퍼를 설계
액션플랜
1.
python prototyping
(1) 일단 최대한 완성된 라이브러리들을 사용하여 전체 파이프라인을 완성시킨 다음에 하나씩 자체적으로 구현하며 디버깅하는 것이 훨씬 개발 생산성이 높을 것이라는 생각, (2) 최적화 원칙 중 알고리즘 단축에 더욱 집중할 수 있는 언어를 사용하기 위해 python 프로토타이핑을 우선적으로 진행한다.
a.
테스트케이스 작성 및 정답 계산 @9/19/2022 → 10/4/2022
i.
1개 이미지, 10개 @9/20/2022
ii.
간단한 산식 동작 확인 @9/20/2022
iii.
전체 데이터셋(gt) 분석 @9/20/2022, @9/21/2022
iv.
알고리즘 구현 @9/21/2022, @9/22/2022
v.
벤치마킹 @9/22/2022
b.
라이브러리 사용해서 속도 향상 @9/23/2022
i.
입출력 결과 확인 @9/26/2022
ii.
벤치마킹 @9/26/2022
c.
라이브러리 제거하고 직접 구현 @9/27/2022
i.
polygon 제거 @9/30/2022
ii.
입출력 결과 확인 @9/30/2022
iii.
벤치마킹 @9/30/2022
d.
병렬처리 도입 @10/3/2022
i.
입출력 결과 확인 @10/3/2022
ii.
벤치마킹 @10/4/2022
2.
C/C++ porting
C/C++ 포팅은 진행 중, 더 급한 일들이 생겨서 더이상 진행하지 않았다.
a.
C/C++ 로 구현
i.
입출력 결과 확인 @10/5/2022
ii.
벤치마킹
b.
병렬처리 라이브러리 도입
i.
입출력 결과 확인
ii.
벤치마킹
알고리즘
•
알고리즘 시간복잡도 단축을 위한 데이터 및 문제 명세
◦
gt (groundtruth) 데이터셋은 개의 이미지 각각에 대해 개씩 정답값을 가지고 있다. 따라서 약 개의 gt 레코드가 존재한다.
◦
pred (prediction) 데이터셋은 개의 이미지 각각에 대해 개씩 예측값을 내놓고 있다. 따라서 약 개의 pred 레코드가 존재한다.
◦
하나의 이미지에서 일어나는 개의 예측과, 해당 이미지에 존재하는 개의 정답값을 매칭시켜 주어야 한다. 매칭 기준은 예측 polygon 과 정답 polygon 의 IoU (Intersection of Union) 이다. 모든 경우를 고려하면 하나의 이미지에 대해서도 의 시간복잡도를 가지게 된다.
◦
문제 접근
▪
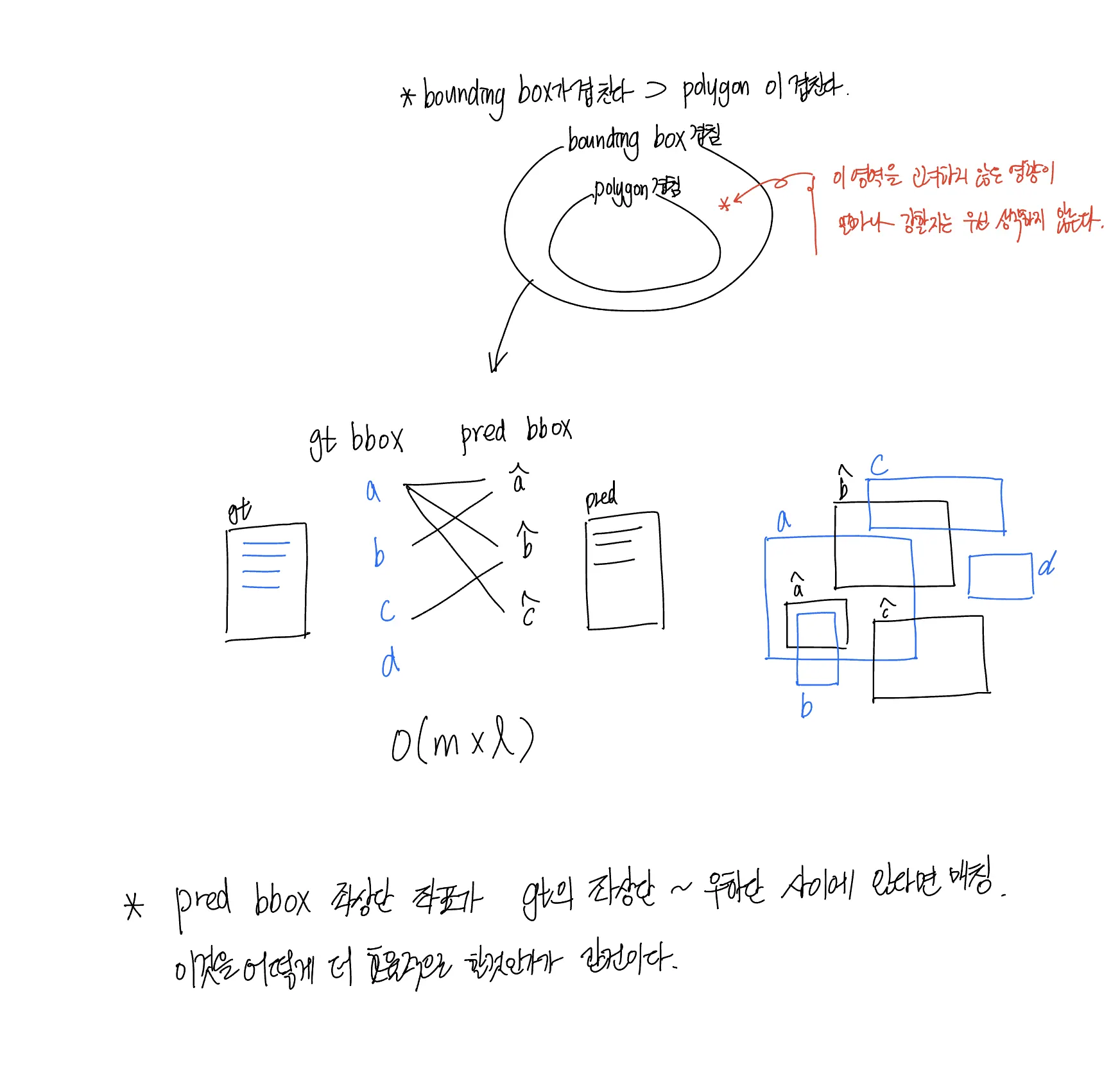
polygon 으로 사고를 전개하면 너무 복잡해진다. 문제를 효율적으로 해결하는 데 집중하기 위해 사고를 조금 단순화할 필요가 있다. 데이터셋에 포함되어 있는 bbox (bounding box) 에 대한 정보를 이용한다. 이 bbox 는 polygon (아래 표에서 segmentation) 을 완전히 포함하고 이미지의 x 축 또는 y 축과 평행한 선분으로 이루어진 직사각형이다.
두 bbox 의 IoU 가 50% 을 넘는 것은 두 polygon 의 IoU 가 50% 을 넘는 것과 상관이 없다.
•
알고리즘들
◦
공통적으로 사용하는 용어
▪
gt.bbox 는 OCR 문제에서 문자 존재영역이 레이블링된 polygon 을 완전히 포함하는 bbox 이다.
▪
pred.bbox 는 OCR 문제의 문자 존재영역 예측 polygon 을 완전히 포함하는 bbox 이다.
▪
gt 와 pred 는 bbox 나 polygon 에 대한 정보를 모두 저장하고 있는 일종의 노드이다.
a.
Alg: naive approach
•
용어
a.
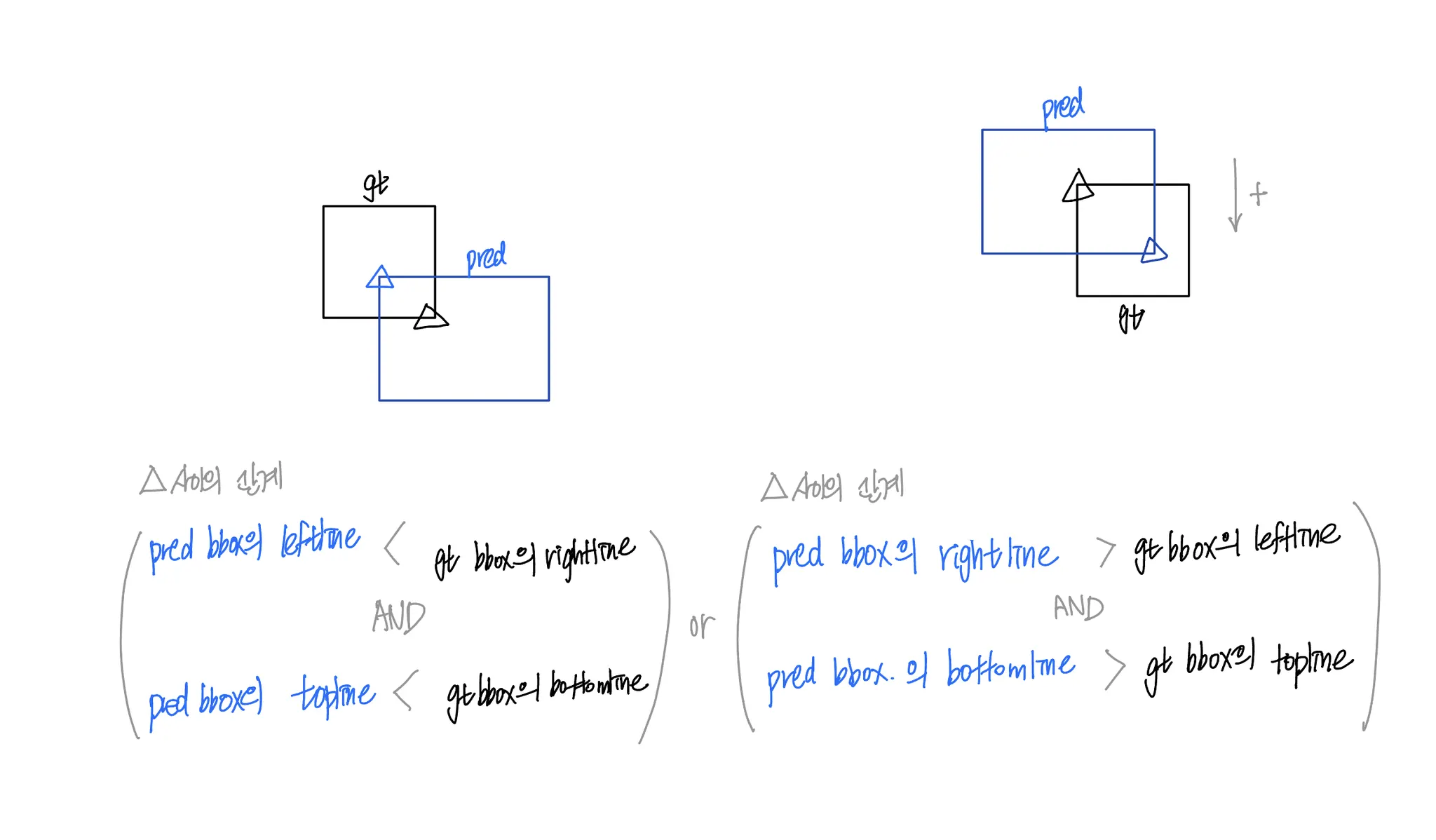
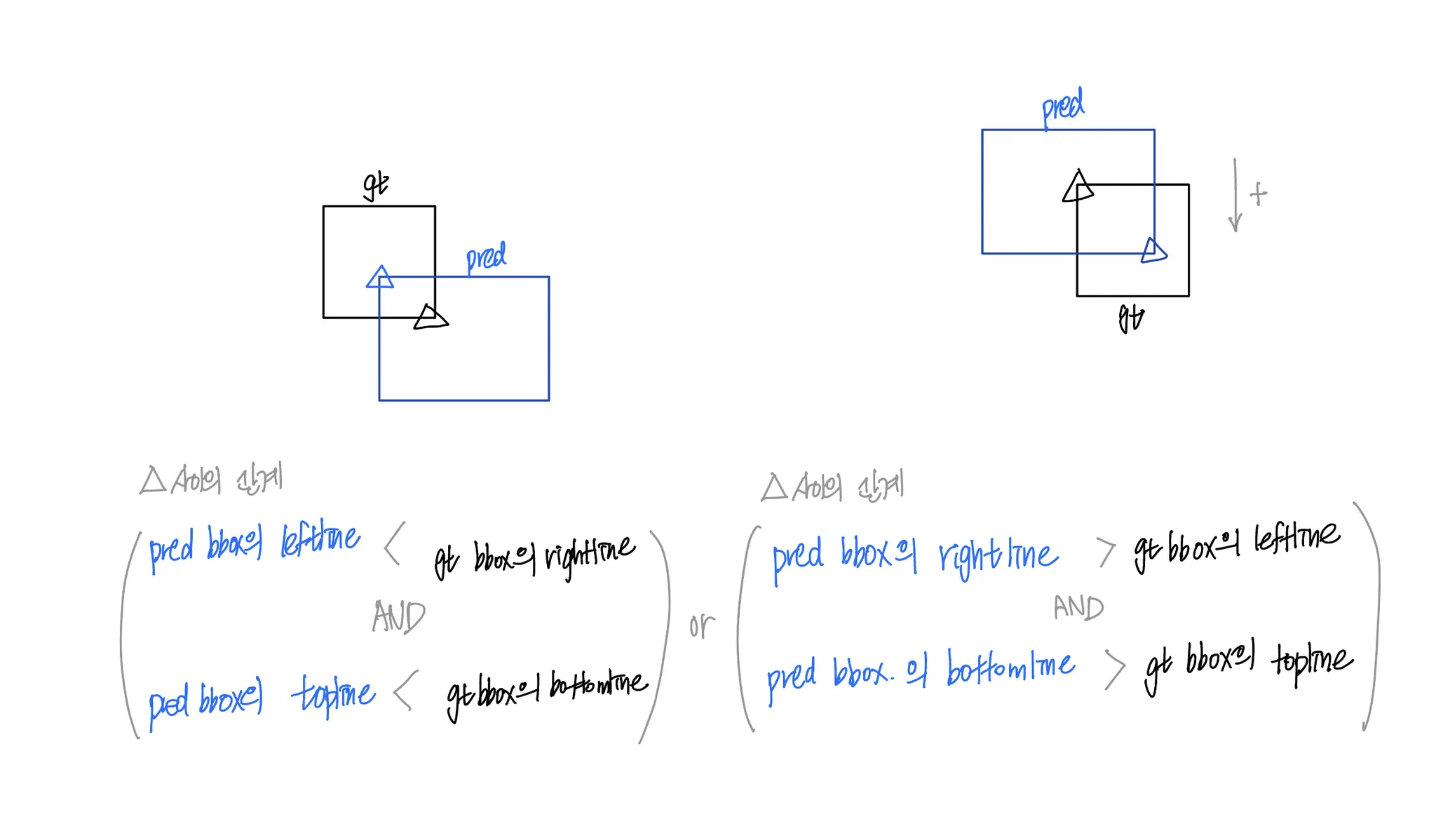
pred 의 right_bottom 의 x 좌표가 gt 의 left_top 의 x 좌표보다 큰 경우
b.
pred 의 right_bottom 의 y 좌표가 gt 의 left_top 의 y 좌표보다 큰 경우
c.
pred 의 left_top 의 x 좌표가 gt 의 right_bottom 의 x 좌표보다 작은 경우
d.
pred 의 left_top 의 y 좌표가 gt 의 right_bottom 의 y 좌표보다 작은 경우
pred.bbox 와 gt.bbox 가 (a and b) or (c and d) 을 만족하면 pred.polygon 과 gt.polygon 을 비교해볼 필요가 생긴다.
두 polygon 의 IoU 를 계산하는 작업은 상당히 무겁다. bbox 정보를 이용하여 무거운 작업의 실행 횟수를 조금이라도 줄이기 위해 사용한다.
•
절차
◦
의사코드
for pred in predictions: // O(l)
for gt in gts: // O(m)
if self.is_intersect(pred.bbox, gt.bbox):
if IoU(pred.polygon, gt.polygon) > 50%:
pair.append(tuple(pred, gt)
C
복사
▪
•
▪
직관적이지만 매우 느림
•
구현
◦
아래 구현에서 pred 와 gt 는 bbox 에 대한 정보는 물론 polygon 에 대한 정보도 담고 있다. self.is_matched 메서드는 두 polygon 의 IoU 를 확인하고 transcription equal 을 확인한다.
class ApproachNaive(Approach):
def run(self):
for pred in self.preds:
for gt in self.gts:
if self.is_matched(pred, gt):
self.add_pair(pred, gt)
Python
복사
b.
Alg: sorting approach
•
용어
◦
gt 들의 집합 gts 를 다음과 같은 기준으로 정렬해 각각의 변수에 저장한다.
▪
gt_left_sorted: gt.bbox 의 left_top 의 x 좌표를 기준으로 오름차순 정렬
▪
gt_top_sorted: gt.bbox 의 left_top 의 y 좌표를 기준으로 오름차순 정렬
▪
gt_right_sorted: gt.bbox 의 right_bottom 의 x 좌표를 기준으로 오름차순 정렬
▪
gt_bottom_sorted: gt.bbox 의 right_bottom 의 y 좌표를 기준으로 오름차순 정렬
각각은 gt 들의 포인터만 연결 리스트 형태로 보관할 뿐, 완전복사(value copy)가 아니다. 집합 gts 의 원소의 개수가 개라고 할 때, 시간복잡도는 이다.
•
절차
1.
예측값들의 집합 preds 의 모든 원소 pred 각각에 대해, pred 이 다음 조건 각각을 부합하는지 검사하고, 부합하는 경우 각각의 리스트에 (gt, pred) 쌍을 저장한다.
a.
pred 의 right_bottom 의 x 좌표가 gt 의 left_top 의 x 좌표보다 큰 경우
b.
pred 의 right_bottom 의 y 좌표가 gt 의 left_top 의 y 좌표보다 큰 경우
c.
pred 의 left_top 의 x 좌표가 gt 의 right_bottom 의 x 좌표보다 작은 경우
d.
pred 의 left_top 의 y 좌표가 gt 의 right_bottom 의 y 좌표보다 작은 경우
이때 gt 는 정렬이 되어 있는 상태이므로, 이진 탐색을 수행한다. 집합 preds 의 원소의 개수가 개라고 했을 때 시간복잡도는 이다.
생각의 편의를 위해서 지금까지는 gts 를 정렬하고, preds 들을 하나하나 비교하는 전략을 사용했다. 하지만 gts 를 먼저 정렬하고 preds 가 적절한 gt 를 찾아나서는 경우 시간복잡도는 인 데 반해, preds 를 먼저 정렬하고 gts 가 적절한 pred 를 찾아나서는 경우의 시간복잡도는 이다. bounding box 를 찾는 task 에서는 일반적으로 NMS 등을 거치기 전 인 특징이 있으므로, gts 를 먼저 정렬하는 편이 preds 를 먼저 정렬하는 편보다 낫다.
2.
위 조건들에 부합한 내용들 중에서, (a and b) or (c and d) 인 쌍들을 찾는다.
•
해시를 이용해 검사한다. 시간복잡도는 이다.
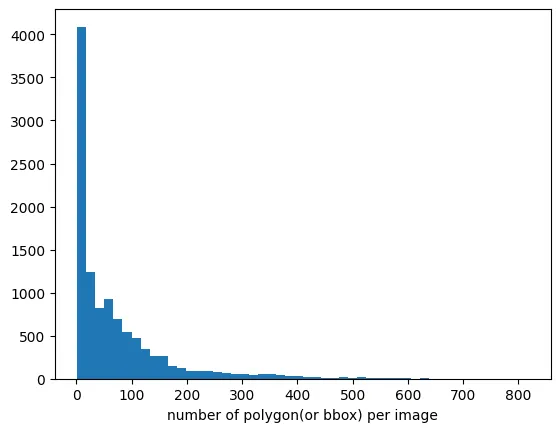
EDA 를 통해 알아보았듯이, 70%가 넘는 경우 gts 는 이미지당 100개가 채 안 되는 경우가 많았다. 이정도라면 충분히 해시가 감당할 수 있을 것이라는 생각이 들었다. LEAN 하게 python 의 set() 이나 dict() 를 이용해 중복검사를 수행할 수 있다(참고5).
3.
매칭된 쌍들을 기준으로 다양한 matrix 를 계산해낸다.
•
구현
◦
아래 구현에서 pred 와 gt 는 bbox 에 대한 정보는 물론 polygon 에 대한 정보도 담고 있다.
◦
gt.cond_intersect() 는 polygon 비교 이전에 bbox 비교를 통해 비교해볼만한 대상을 포함하고 있다. self.is_matched 메서드는 두 polygon 의 IoU 를 확인하고 transcription equal 을 확인한다.
class ApproachSort(Approach):
def run(self):
pred_sorted_left = self.sorted(self.preds, key=lambda node: node.left_top[0])
pred_sorted_top = self.sorted(self.preds, key=lambda node: node.left_top[1])
pred_sorted_right = self.sorted(self.preds, key=lambda node: node.right_bottom[0])
pred_sorted_bottom = self.sorted(self.preds, key=lambda node: node.right_bottom[1])
self.binary_search_by_sorted_preds(pred_sorted_left, self.gts, cond='right')
self.binary_search_by_sorted_preds(pred_sorted_top, self.gts, cond='bottom')
self.binary_search_by_sorted_preds(pred_sorted_right, self.gts, cond='left')
self.binary_search_by_sorted_preds(pred_sorted_bottom, self.gts, cond='top')
for gt in self.gts:
for e in gt.cond_intersect():
if self.is_matched(e, gt):
self.add_pair(e, gt)
def binary_search_by_sorted_preds(self, sorted_preds, gts, cond):
def condition(pred, gt, cond):
if cond == 'left':
return pred.left_top[0] < gt.right_bottom[0]
elif cond == 'top':
return pred.left_top[1] < gt.right_bottom[1]
elif cond == 'right':
return pred.right_bottom[0] > gt.left_top[0]
elif cond == 'bottom':
return pred.right_bottom[1] > gt.left_top[1]
def fill(gt, pred, cond):
if cond == 'left':
gt.add_candidate_filtered_by_left(pred)
elif cond == 'top':
gt.add_candidate_filtered_by_top(pred)
elif cond == 'right':
gt.add_candidate_filtered_by_right(pred)
elif cond == 'bottom':
gt.add_candidate_filtered_by_bottom(pred)
for gt in gts:
_l = 0
_r = len(sorted_preds)
while _l < _r:
_mid = (_l + _r) // 2
if condition(gt, sorted_preds[_mid], cond):
_l = _mid + 1
else:
_r = _mid
for pred in sorted_preds[:_l]:
fill(gt, pred, cond)
Python
복사
•
두 접근의 실제 실행시간 비교
Image ID: 17
Naive Approach start.
# of preds: 1000
# of gts: 647
.. O(n^2) total dt: 42.19(s)
... Found 0 pairs.
Sort based Approach start.
# of preds: 1000
# of gts: 647
.. O(nlog(n)) total dt: 30.87(s)
... Found 0 pairs.
Python
복사
•
테스트
◦
피드백: polygon iou 를 계산하기 전에 다른 기준으로 iou를 비교해서 한번 걸러내 주는 아이디어 자체에 문제가 있다. Polygon 에는 이미 선분들이 있고, 이들의 교점만 확인해 보아도 두 polygon 의 IoU 를 계산해볼 필요가 있는지 없는지 알 수 있다. 그런데 bbox 를 이용해 다시한번 확인해보아야 하는 polygon 을 저장해 두었다가 이들 전체를 다시 확인하는 과정이 상당히 무거울 것이다. 물론, 대부분의 문자 영역 polygon 이 직사각형 bbox 형태로 제공되고 bbox 들이 겹치는 경우가 많이 없다면(sparse 한 경우) 빠르게 동작할지도 모른다. 하지만 차라리 iou 를 계산하는 도중에 선분의 교차 등을 확인하는 단계에서 골라내는 것이 나을지도 모른다.
Aihub 과제의 금융 OCR, 물류 OCR 데이터의 경우 모든 polygon 이 직사각형 형태로 제공된다. 즉, left top 과 right bottom 포맷으로 제공되어도 전혀 차이가 없을 레이블을 제공하고 있다. 또한, 이들 데이터 특성상 polygon 들의 크기가 작고 겹치는 경우가 거의 없다. 이런 경우에는 굉장히 빨리 동작할 수 있다. 따라서 추가적으로 수정하지 않는다.
상수시간 줄이기
•
앞서 설명한 두 가지 접근 중 sorting approach 의 시간 분석을 보자.
Image ID: 17
...
Sort based Approach start.
# of preds: 1000
# of gts: 647
.. sorting dt: 0.001(s)
.. filtering dt: 1.938(s)
.. matching dt: 28.590(s)
.. O(nlog(n)) total dt: 30.53(s)
... Found 0 pairs.
Python
복사
•
matching 단계의 연산시간이 매우 높음을 알 수 있다.
◦
matching 단계에서는 두 polygon 의 IoU 를 계산한다.
•
이것은 시간복잡도나 해시충돌 때문이 아니다. 이것은 python 의 연산속도 문제이다.
◦
이렇게 생각한 증거들은 다음과 같다.
1.
항상 matching 단계에서는 filtering 단계의 14배~15배정도의 연산시간을 가진다. 만약 시간복잡도 문제였으면 이나 값이 변경될 때마다 이 배수가 일정하지 않았을 것이다.
Image ID: 13
Naive Approach start.
# of preds: 1000
# of gts: 13
.. matching dt: 0.966(s)
.. O(n^2): 13000, dt: 0.97(s)
... Found 1 pairs.
Sort based Approach start.
# of preds: 1000
# of gts: 13
.. sorting dt: 0.002(s)
.. filtering dt: 0.051(s)
.. matching dt: 0.909(s)
.. O(nlog(n)): 0, dt: 0.96(s)
... Found 1 pairs.
Python
복사
Image ID: 17
Naive Approach start.
# of preds: 1000
# of gts: 647
.. matching dt: 41.761(s)
.. O(n^2): 647000, dt: 41.76(s)
... Found 0 pairs.
Sort based Approach start.
# of preds: 1000
# of gts: 647
.. sorting dt: 0.001(s)
.. filtering dt: 1.938(s)
.. matching dt: 28.590(s)
.. O(nlog(n)): 435273, dt: 30.53(s)
... Found 0 pairs.
Python
복사
2.
연산집약적 코드(case1)를 제거했을 때(case2) 시간이 매우 단축된다.
•
case1 : matrix.cal_iou 의 시간복잡도는
def is_matched(self, pred:Node, gt:Node):
if matrix.cal_iou(pred.polygon, gt.polygon) > 0.5:
return True
else:
return False
Python
복사
Image ID: 17
...
Sort based Approach start.
# of preds: 1000
# of gts: 647
.. sorting dt: 0.002(s)
.. filtering dt: 2.239(s)
.. matching dt: 30.399(s)
.. O(nlog(n)): 0, dt: 32.64(s)
... Found 0 pairs.
Python
복사
•
case2
def is_matched(self, pred:Node, gt:Node):
return True
Python
복사
Image ID: 17
...
Sort based Approach start.
Removed Computationally Intensive Code
# of preds: 1000
# of gts: 647
.. sorting dt: 0.001(s)
.. filtering dt: 2.245(s)
.. matching dt: 0.797(s)
.. O(nlog(n)): 0, dt: 3.04(s)
... Found 0 pairs.
Python
복사
3.
해시 충돌이 날만한 부분을 제거해도 연산시간은 동일하다.
•
python 의 연산 속도를 단축시킬 수 있는 방법들은 다음과 같다.
1.
일단 그 코드를 최대한 실행하지 않도록 만드는 방법이다. 예를 들어, polygon1 의 area 가 polygon2 의 area 의 2배가 넘으면, 죽었다 깨어나도 iou 가 0.5 를 넘을 수가 없다. 그런 것들은 아예 intersect() 나 union() 등 무거운 연산을 시작하지도 않도록 만들어버리면 좋다.
----- Image ID: 17 -----
Naive Approach start.
python only
# of preds: 1000
# of gts: 647
.. matching dt: 7.182(s)
Python
복사
2.
연산집약적 코드의 속도를 향상시키는 방법
•
•
•
•
파이썬 돌리는데 고양이가 이렇게 열심히 뛰는거 처음 봤다.
벤치마킹 결과
it/s 는 1초당 image 1장에 해당하는 preds 와 gts 를 처리할 수 있는 양에 해당합니다.
•
10 images, 10000 preds (1000 preds/image), 202 gts
◦
약 50배 성능 향상
single core | native python | polygon lib | numba optimized |
alg: naive | 0.21it/s | - | 1.46it/s |
alg: sort | 0.27it/s | - | 2.56it/s |
multi(10) core | native python | polygon lib | numba optimized |
alg: naive | 1.54it/s | - | 7.96it/s |
alg: sort | 1.99it/s | - | 10.39it/s |
•
50 images, 50,000 preds (1000 preds/image), 3139 gts
◦
약 90배 성능 향상 (괄호는 프로그램이 종료하는 사건까지 걸린 시간)
single core | native python | polygon lib | numba optimized |
alg: naive | 0.11it/s (7:16) | 0.21it/s (3:56) | 1.44it/s (0:34) |
alg: sort | 0.14it/s (5:54) | 2.56it/s (3:14) | 1.32it/s (0:37) |
multi(10) core | native python | polygon lib | numba optimized |
alg: naive | 1.45it/s (0:34) | 2.05it/s (0:24) | 8.56it/s (0:05) |
alg: sort | 1.86it/s (0:26) | 2.62it/s (00:19) | 9.82it/s (0:05) |
•
50 images, 500,000 preds (10,000 preds/image), 3271 gts
multi(10) core | native python | polygon lib | numba optimized |
alg: naive | - | - | 0.86s/it (0:57) |
alg: sort | - | - | 1.02it/s (0:48) |
•
50 images, 5,000,000 preds (100,000 preds/image), 3271 gts
multi(10) core | native python | polygon lib | numba optimized |
alg: naive | - | - | 11.82s/it (9:51) |
alg: sort | - | - | 10.28s/it (8:34) |
◦
과 의 실행시간에 큰 차이가 나지 않는 이유는, naive 접근과 sort 접근은 모두 bbox 를 통해 ‘계산할 가치가 있는 다각형’ 을 필터링해내는 방식으로 작동하는데 이때 필터링되는 bbox 의 개수는 비슷하기 때문임. sorting 과 filtering (시간복잡도에 영향을 받음) 에 걸리는 시간보다 matching 에서 소비되는 시간이 훨씬 길기 때문일 것이라고 추측.
•
10892 images, 10,892,000 preds (1000 preds/image), 785,498 gts
◦
돌릴 엄두가 안난다.
single core | native python | polygon lib | numba optimized |
alg: naive | |||
alg: sort |
multi(10) core | native python | polygon lib | numba optimized |
alg: naive | 13.49it/s (13:27) | ||
alg: sort | 15.62it/s (11:37) |
여기까지만 했는데도 처음에 비해 속도가 너무 빨라져서, 로우레벨 최적화를 더 해야 하는건지 모르겠다.
피드백: 이미 엄청 빨라졌지만 C로 하면 신세계를 보게 될 것이다. 아무리 JIT 라도 그래도 네이티브보다 빠를수는 없지 않은가.
•
께 진행상황을 보고할 때 사용했던 글들
◦