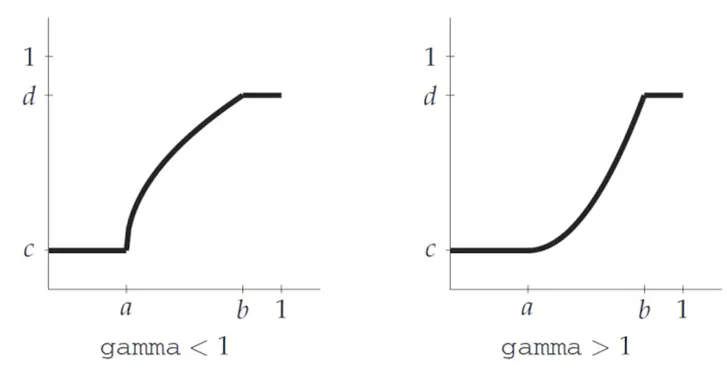Search
4️⃣

화소 단위 영상처리 연산과 히스토그램

•
2021/02/18~2021/02/23, 2023/10/18~2023/10/20

영상처리 연산

영상의 화소(pixel)값을 변경하는 일을 영상처리 연산이라고 한다.
•
화소 단위 처리: 하나의 화소값만을 사용하여 화소값을 변경
•
영역 단위 처리: 이웃 화소들을 참조하여 화소값을 변경
•
영상 단위 처리: 기하적 변환(Transform)

화소 단위 처리

•
화소 단위 처리는 화소 단위 처리 함수 ff를 정의하는 일이다.
dst(x,y)=f(src(x,y))dst(x,y)=f(src(x,y))
•
반올림, 덧셈, 뺄셈, 곱셈, 나눗셈
◦
클리핑(clipping): 함수의 결과가 지정한 범위 0~255 를 벗어나는 경우, 반올림한 후 잘라내는 것.
▪
x < 0 이면 x = 0
▪
x > 255 이면 x = 255
▪
클리핑 연산은 포화(saturate), 리미트(limit) 연산이라고 부르기도 한다.
C++ OpenCV에서는 덧셈, 뺄셈 연산이 영상 객체에 대해 오버로딩되어 있다. 오버로딩된 연산자를 이용해 연산을 수행하면 클리핑이 자동으로 수행된다.
•
반전(inverse)
f(p)=255−pf(p)=255-p
덧셈과 뺄셈
곱셈과 나눗셈
b5 의 경우에는, b5 * 0.5 + 128 의 결과물 이다. 0.5 로 나누는 순간 소수점을 달고 있는 화소값들이 생기는데, 이 화소값들에 rounding 처리를 하게 되면서 정보 손실이 일어날 수밖에 없다.
뺄셈과 곱셈 연산, 보수 (complement) 연산

히스토그램(histogram)

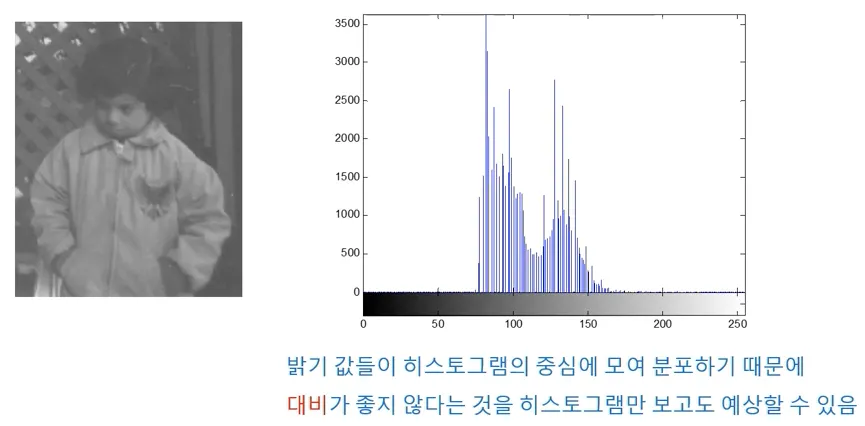
각 밝기값이 영상에서 존재하는 개수를 나타내는 그래프를 의미한다.
히스토그램을 기반으로 영상의 외관에 대한 정보를 추론할 수 있다.
•
화소들의 밝기값이 낮은 영역에 분포하면, 어두운 영상
•
화소들의 밝기값이 높은 영역에 분포하면, 밝은 영상
•
화소들의 밝기 값이 넓은 범위에 걸쳐 분포하면, 대비(contrast)가 좋은 영상

히스토그램 스트레칭(histogram stretching)

•
화소들의 밝기 값이 넓은 범위에 걸쳐 분포하는 영상이 대비(contrast)가 좋은 영상이라고 했다.
•
대비가 좋지 않은 영상을 대비가 좋은 영상으로 만들어 줄 필요가 있다.
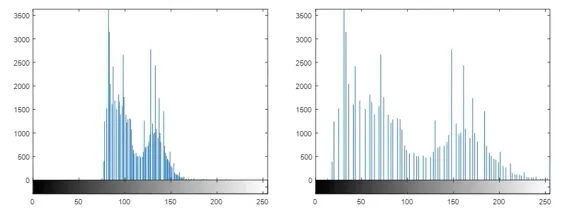
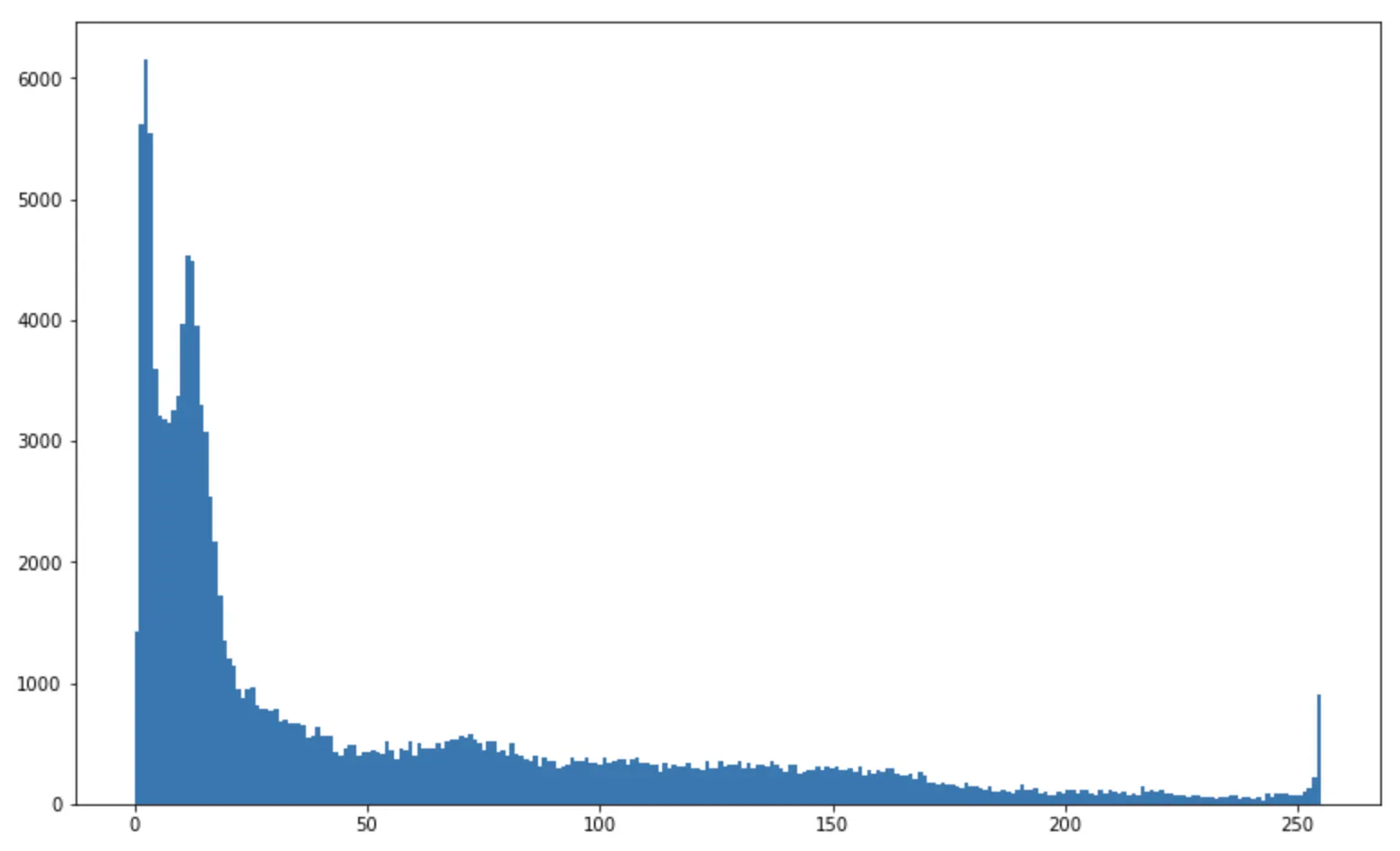
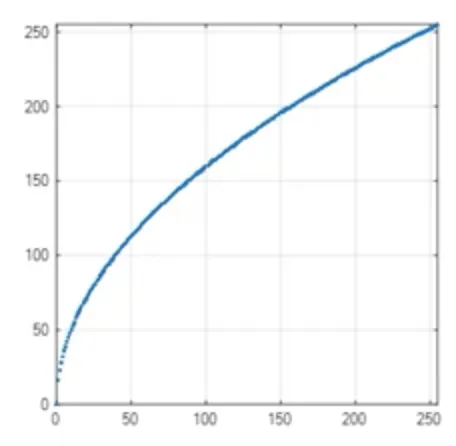
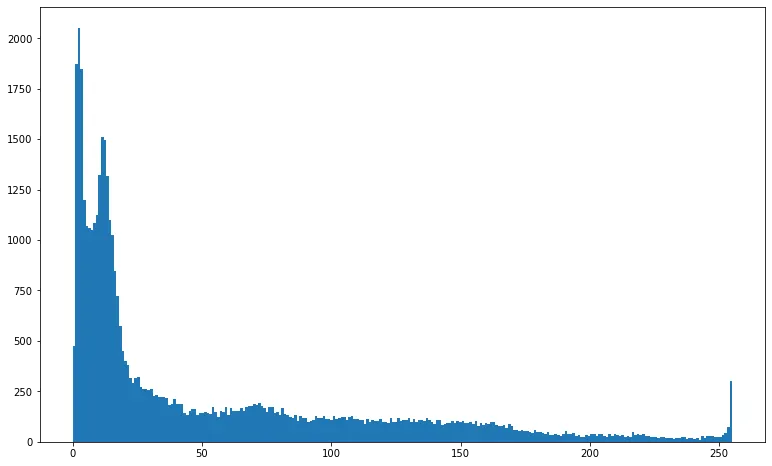
좌: 원래 이미지의 히스토그램, 중앙: y 축은 변환 후의 pixel 밝기, 우: 변환 후 영상의 히스토그램
히스토그램을 펼쳐(stretching) 밝기값이 히스토그램 전 구간에서 나타나도록 변환하는 기법을 히스토그램 스트레칭(histogram stretching)이라고 한다.
히스토그램 스트레칭도 결국 적절한 화소 단위 처리 함수 ff를 만드는 일이다.
piecewise linear
•
히스토그램 스트레칭에 사용할 함수 ff로 어떤 것을 선택하는지는 개인의 자유다.
•
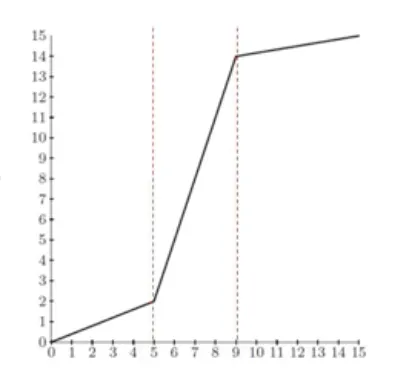
가장 간단한 ff는 직선의 방정식과 클리핑에 따라 다음과 같다.
f(p)={0p<m(I)f(p)=255M(I)−m(I)(p−m(I))m(I)≤p≤M(I)1M(I)<pf(p) = \begin{cases}% 0 &\qquad\text{} p < m(I)\\ f(p)=\frac{255}{M(I)-m(I)}(p-m(I)) &\qquad\text{} m(I) \leq p \leq M(I) \\ 1 &\qquad\text{} M(I) < p\\ \end{cases}
•
조금 더 복잡하게, xx축의 a,ba, b 값은 결국 original_im.min, original_im.max 값이다.
조각조각이 선형인 함수를 부분적 선형함수(piecewise linear)라고 한다.

히스토그램 스트레칭 실습

im_2 = cv2.imread('tire.tif') plt.figure(121, figsize = [13,8]) plt.imshow(im_2)
Python
복사
이미지 불러오기
불러온 이미지
x_range = [0, 255] bins = 2**8 plt.figure(122, figsize = [13,8]) plt.hist(np.ravel(im_2), bins=bins, range=x_range)
Python
복사
히스토그램 시각화
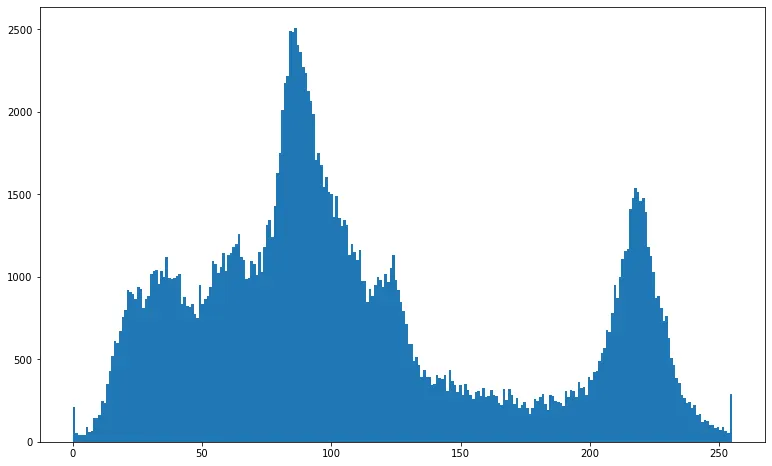
히스토그램
•
이 타이어 이미지의 histogram 은 0부터 255까지의 모든 범위에 걸쳐 있지만, 특히 어두운 부분의 밝기에 화소값들이 몰려 있음을 알 수 있다.
•
화소값이 낮은 부분은 조금 넓게 떨어뜨려 주고, 화소값이 높은 부분은 조금 오밀조밀하게 만들어 주면 좋지 않을까?
a = 0, b = 255, gamma < 1 인 함수 ff가 가장 히스토그램 스트레칭에 효과적일 것이다.
좌: 원본 영상, 우: 히스토그램 스트레칭 후 영상
히스토그램 스트레칭 함수
좌: 원본 영상, 우: 히스토그램 스트레칭 이후 영상

부분적 선형함수(piecewise linear function)를 통한 히스토그램 스트레칭

부분적 선형함수
def hist_stretch_piecewise_linear_f(im, a, b): assert len(a) == len(b), 'vector a, b must be of equal size' print(im.dtype) _im = im.copy() _im = _im.astype(np.float32) print(_im.dtype) is_processed = np.zeros(_im.shape) # if processed once, mark as True, else zero (False) to prevent multiple processing for i in range(1,len(a)): cond = (_im<a[i])*(_im>=a[i-1]) cond = cond * (np.logical_not(is_processed)) #print(cond[100, 100], is_processed[100, 100], a[i], a[i-1], end = ' ') _im[np.where(cond)] = ((b[i]-b[i-1])/(a[i]-a[i-1])) * (_im[np.where(cond)]-a[i]) + b[i] #print('where 100, 100 intensity : ', _im[100, 100]) is_processed = np.logical_or(cond, is_processed) #print(cond[100, 100], is_processed[100, 100], a[i], a[i-1]) _im = _im.astype(np.uint8) print(_im.dtype) #print('where 100, 100 final : ', _im[100, 100]) return _im stretched_im = hist_stretch_piecewise_linear_f(im_2, [0, 10, 20, 40, 255], [0, 50, 90, 130, 255]) plt.figure(141, figsize=[8,8]) plt.imshow(stretched_im, cmap='gray')
Python
복사
소스코드
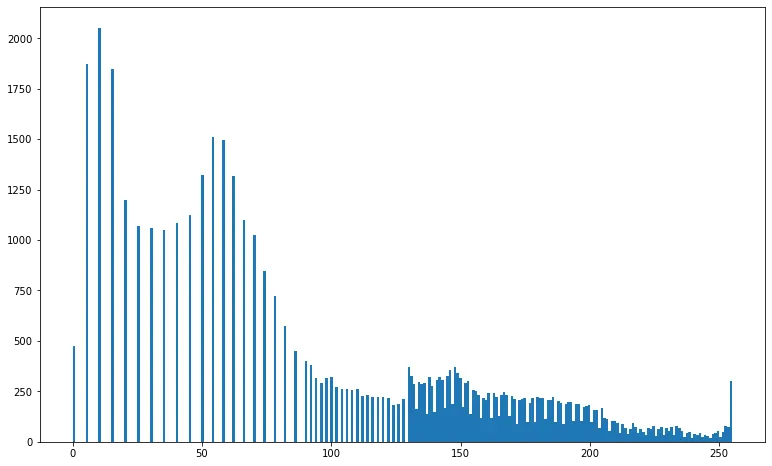
스트레칭 전
스트레칭 후

히스토그램 평활화(histogram equalization)

히스토그램 평활화(histogram equalization)는 자동화된 방법으로 영상 밝기값의 빈도수를 같게 만드는 것을 의미한다.
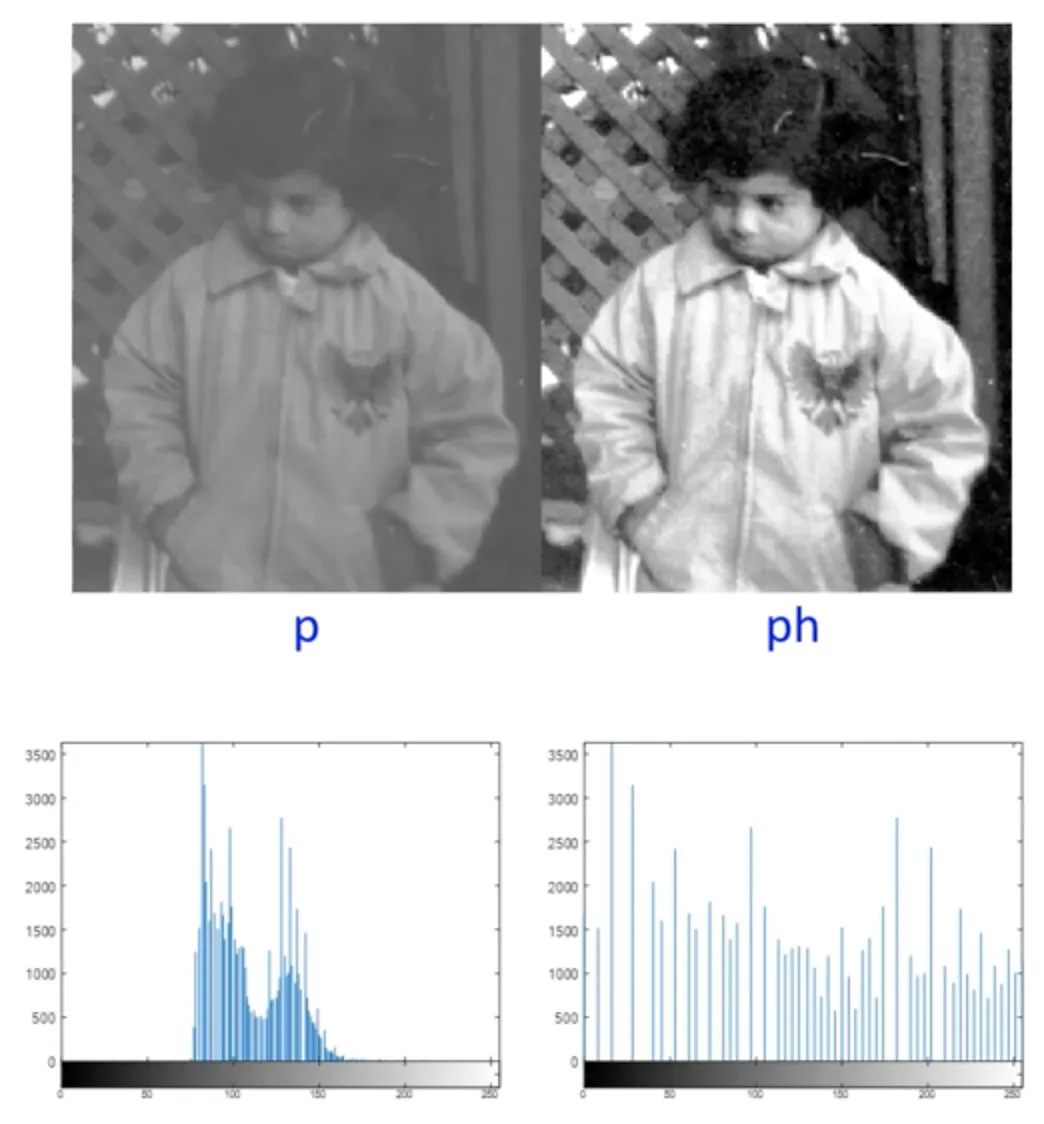
원본 영상(p), 히스토그램 평활화가 적용된 영상(ph)
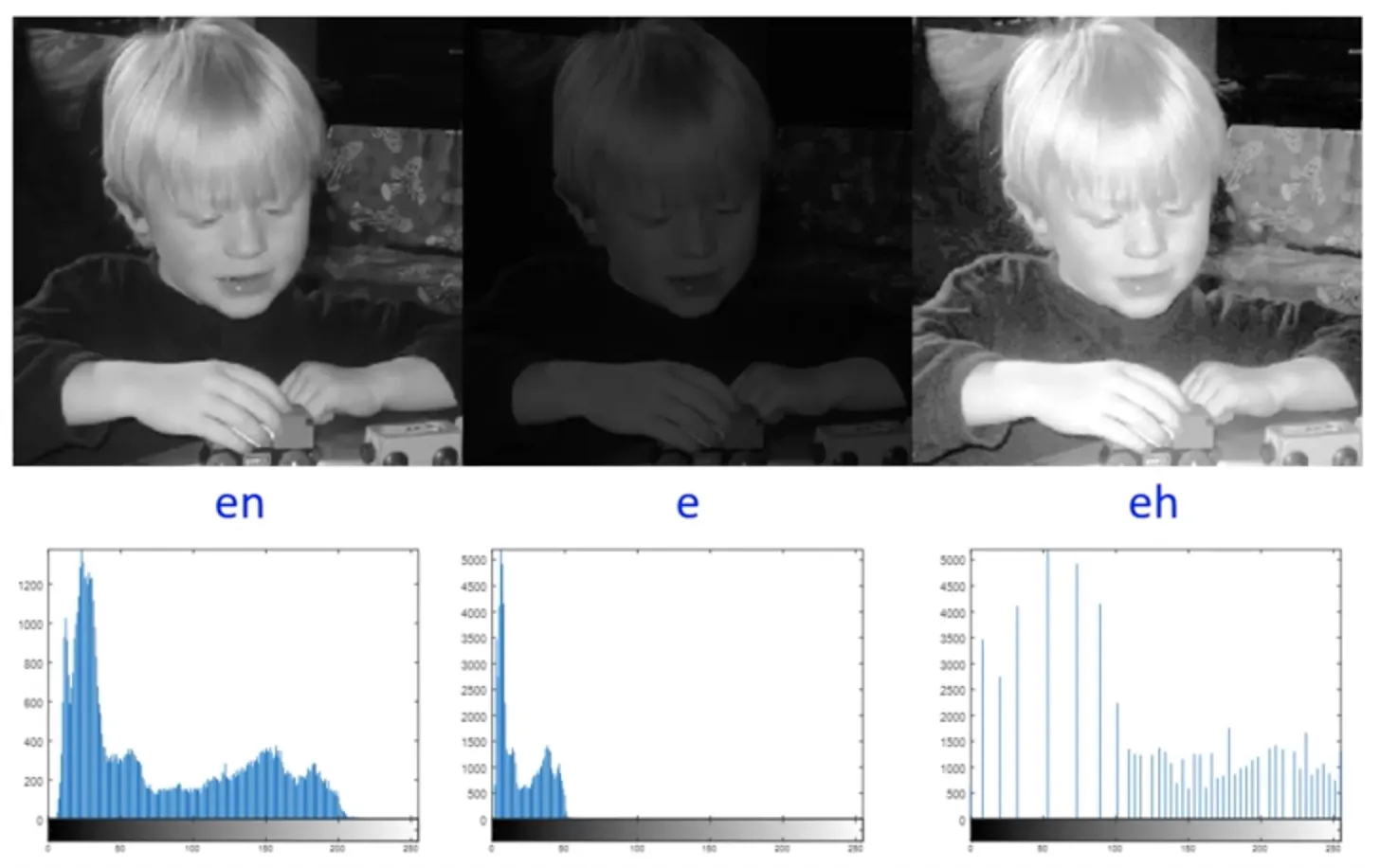
원본 영상(e), 히스토그램 스트레칭이 적용된 영상(en), 히스토그램 평활화가 적용된 영상(eh)
의미적으로 히스토그램 스트레칭은 히스토그램의 형태를 유지하고 최대한 펼치는 개념이고, 히스토그램 평활화는 히스토그램을 최대한 평평하게 만드는 개념이다.
•
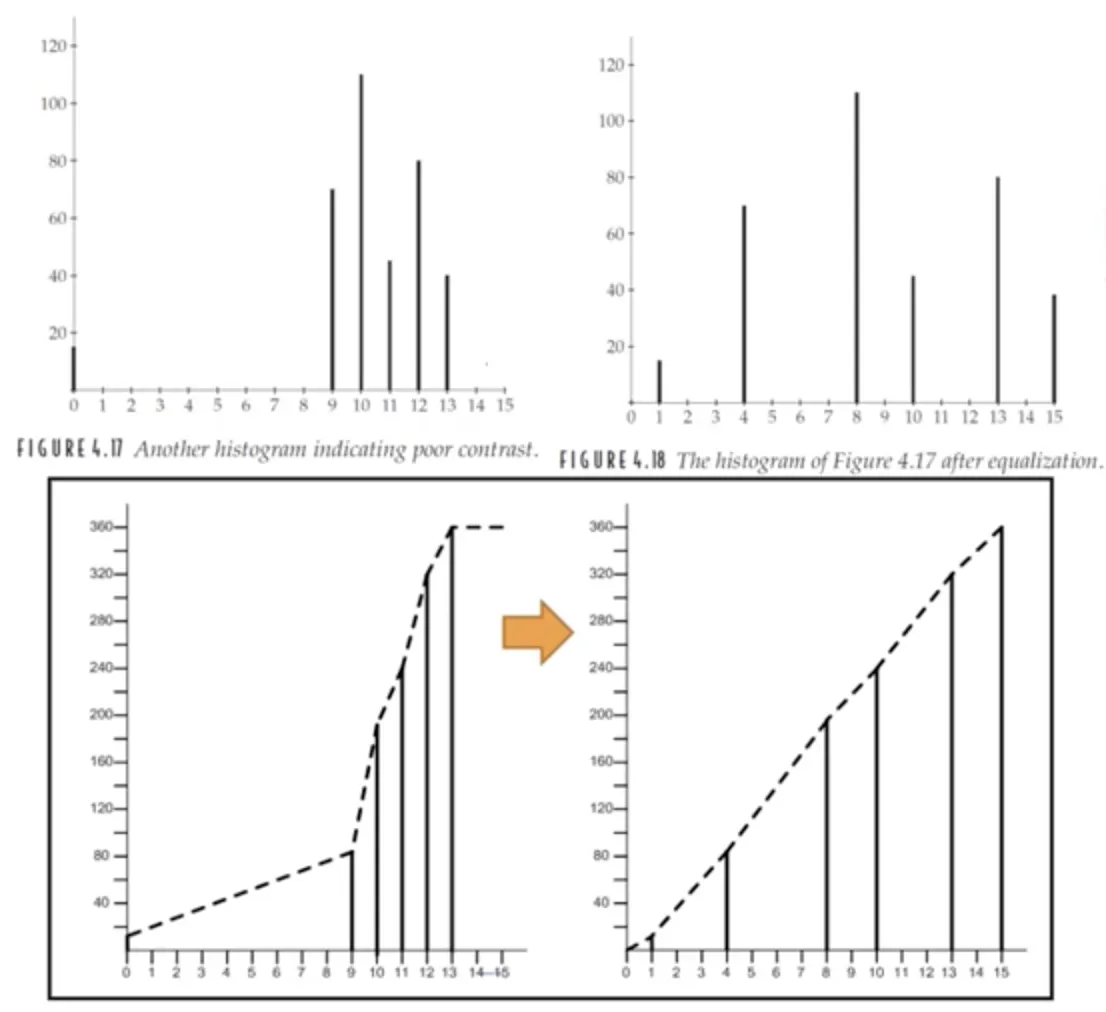
어떤 (19, 19) 크기의 4bit 영상의 히스토그램이 아래와 같다고 하자.
•
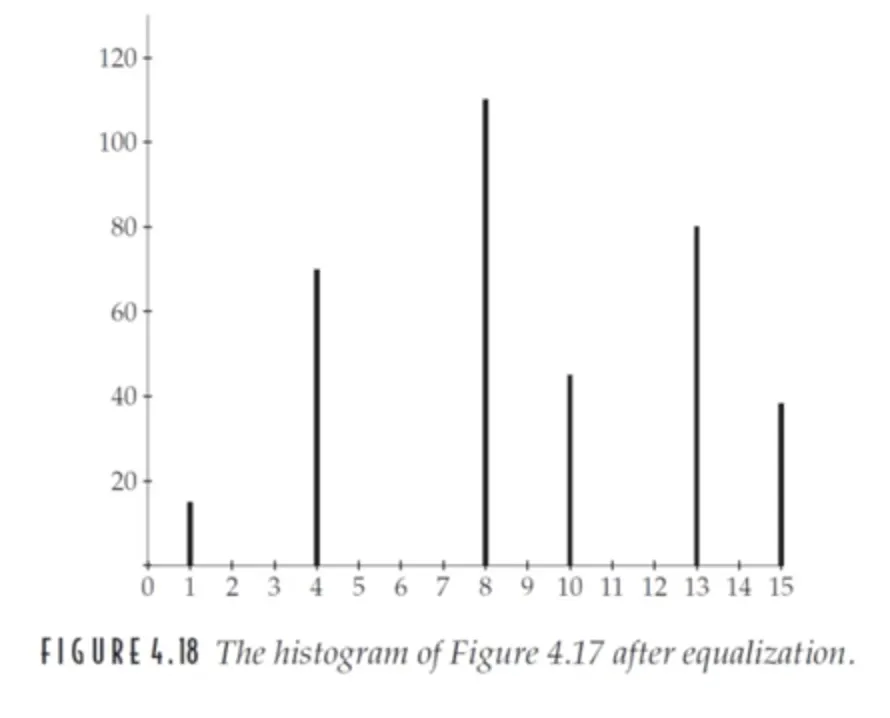
히스토그램 평활화가 수행된 결과는 다음과 같다.
histogram equalization 결과물
•
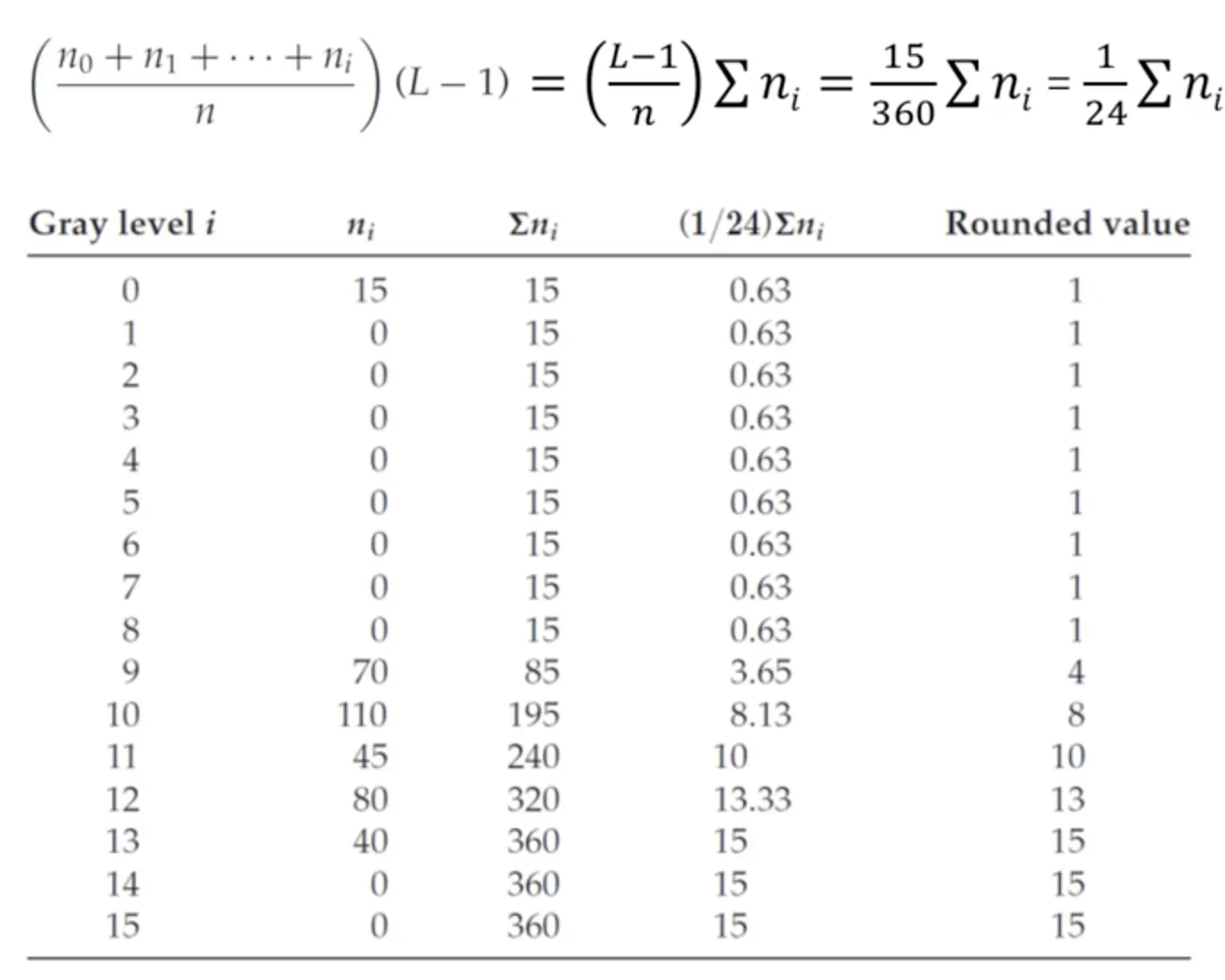
히스토그램 평활화는 누적분포함수를 이용한다.
◦
LL : 가장 밝은 픽셀의 밝기(15)
◦
(n0,n1,...,nin_0, n_1, ..., n_i) : 각 밝기마다 몇 개의 픽셀을 가지는지
◦
nn : 총 픽셀의 개수(360)
Gray level ii 에 해당하는 값이 Rounded value 로 매핑된다.
•
히스토그램 평활화를 수행하는 것도 함수 dst(x,y)=f(src(x,y))dst(x,y)=f(src(x,y))라고 볼 수 있다.
f(p)=round((L−1∑0Lni)∑0pni)f(p)=\text{round}( (\frac{L-1}{{\sum}_0^L n_i}) {\sum}_0^p n_{i} )
•
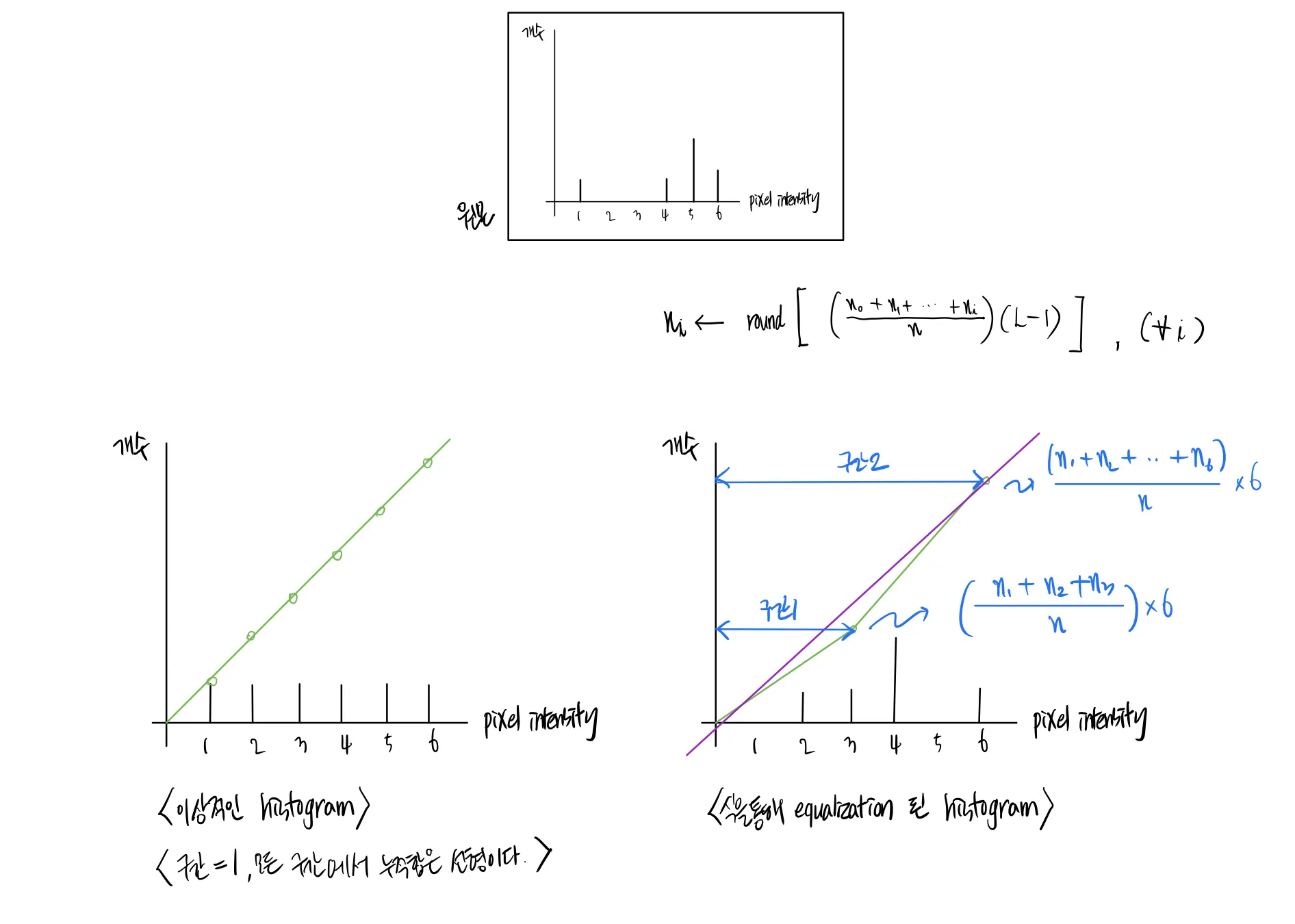
식을 조금 더 잘 이해해 보자.
좌: 이상적인 histogram, 우: 우리가 수행할 수 있는 histogram
◦
앞서 의미적으로 히스토그램 평활화는 히스토그램을 최대한 평평하게 만드는 개념이라고 했다.
◦
이 식이 표현하고자 하는 바는 왼쪽 그림과 같이 이상적인 상태를 흉내내는 것이다.
◦
이상적인 상태란, 모든 밝기를 가지는 픽셀의 수가 완벽하게 동일한 상태이다.
◦
하지만 이미지에서 이상적인 상태로 강제로 히스토그램을 변형하는 것은 불가능하다.
◦
원본 영상에서 각 픽셀의 밝기를 임의로 변형을 해야 하는 상황이 나타나기 때문이다.
◦
히스토그램 평활화는 구간의 누적합을 구간으로 나누어 보았을 때 선형이 되도록 만든다.
좌상: 원본 영상의 히스토그램 우상: 히스토그램 평활화 이후의 히스토그램 좌하 : 좌상단 히스토그램의 누적합 우하: 우상단 히스토그램의 누적합

히스토그램 평활화 실습

import cv2 plt.figure(151, figsize=[8,8]) im_2_eq = cv2.equalizeHist(im_2) plt.imshow(im_2_eq, cmap='gray')
Bash
복사
OpenCV에서는 히스토그램 평활화를 수행하는 equalizeHist함수를 제공한다.
plt.figure(152, figsize = [13,8]) plt.hist(np.ravel(im_2_eq), bins=bins, range=x_range) plt.show()
Bash
복사
히스토그램 평활화가 적용된 영상의 히스토그램 시각화

룩-업 테이블(look-up table, LUT)

룩업 테이블은 밝기값 변환 시 참조를 위해 사용하는 테이블이다.
속도가 매우 중요한 연산을 해야 하는 경우가 발생했을 때 유용하게 사용할 수 있다.
•
매번 연산을 하지 않고, 테이블만 참조해서 밝기값을 변경할 수 있다.
•
이를 왜 사용해야 할까?
◦
어차피 화소단위 처리는 특정 픽셀 강도를 입력받아 해당 적절한 출력값을 내보낸다.
◦
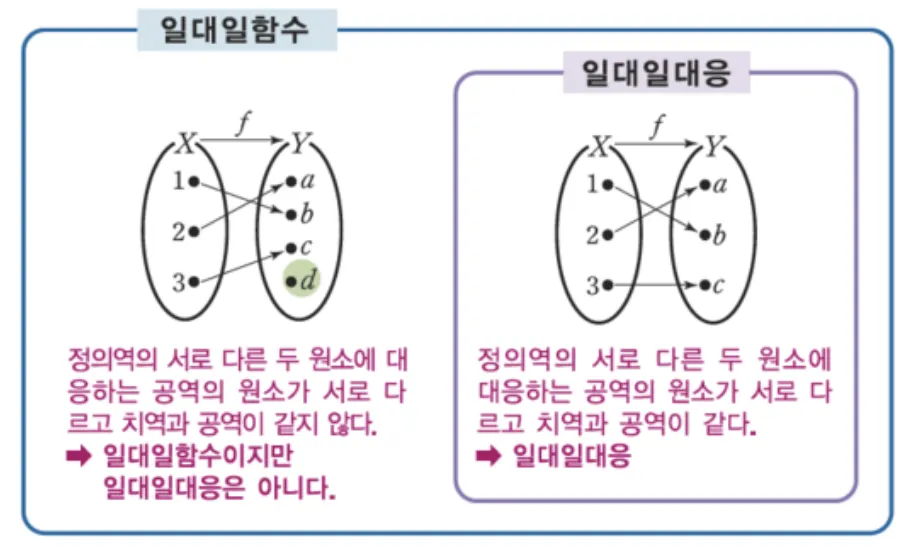
정의역은 0과 255 사이의 정수이고, 치역도 0과 255 사이의 정수인 일대일함수이다.
reminid
•
가령 이런 복잡한 연산이 있다고 생각을 해 보자.
res=round((src∗3)/4+5.55)+...+...)res = \text{round}(\sqrt{(src *3)/4 + 5.55 )} + ... + ...)
◦
연산 과정이 길어지면 길어질수록 오랜 시간이 걸릴 것이다.
◦
결국 이것도 정의역이 [0, 255]이고 치역이 [0, 255]인 함수 y=f(x)y=f(x)로 추상화할 수 있다.
◦
모든 xx에 대해서 f(x)f(x)를 계산해둔 LUT가 있다면 런타임에 O(1)O(1)시간에 수행가능하다.

룩업 테이블 실습

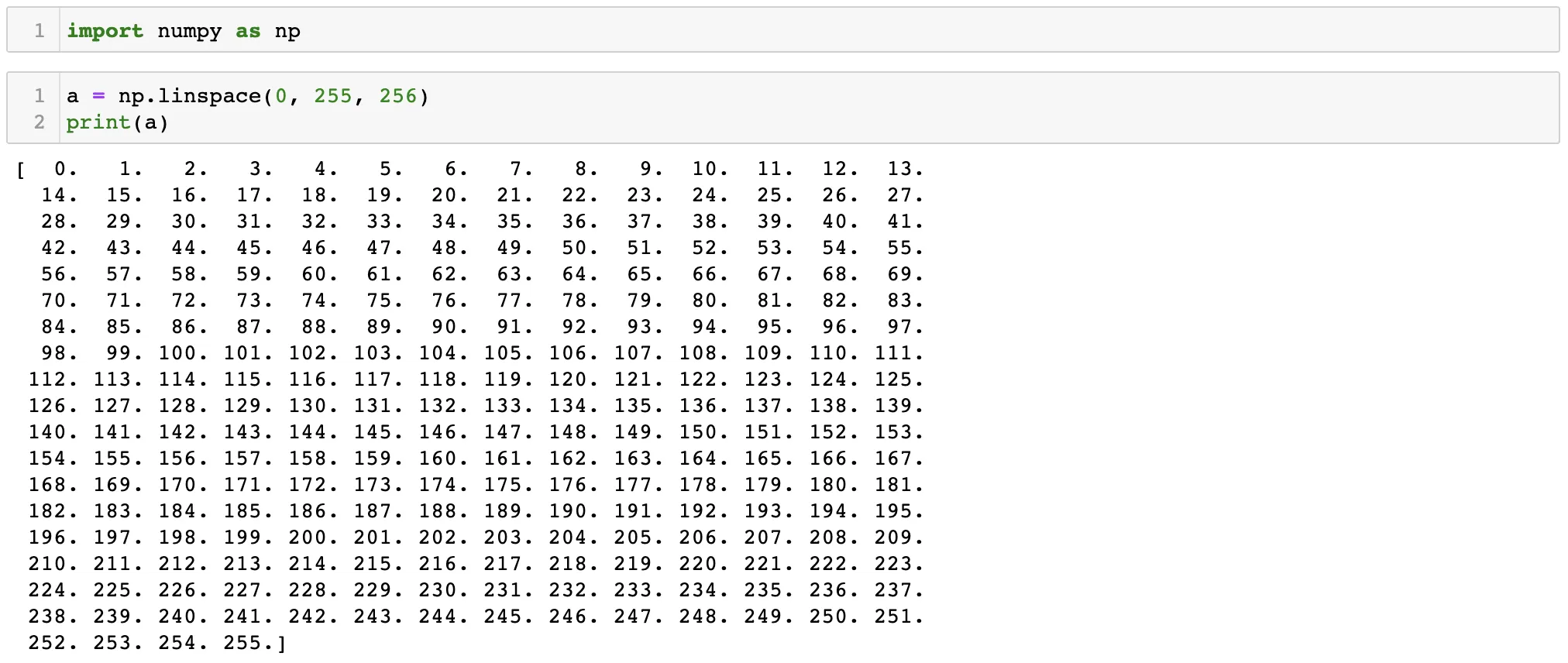
정의역
a[0:96] = (64/96)*a[0:96] a[96:160] = ((192-64)/(160-96))*(a[96:160]-96)+64 a[160:] = ((255-192)/(255-160))*(a[160:]-160)+192 a = a.astype(np.uint8)
Python
복사
치역
import cv2 im = cv2.imread('blocks.tif') plt.figure(121, figsize=[13,8]) plt.subplot(1,2,1) plt.imshow(im) plt.subplot(1,2,2) plt.imshow(a[im]) plt.show()
Bash
복사
룩업테이블을 이용해 화소 단위 영상처리 수행
원본
변환 후