연속함수를 이산함수로 표현하기 위한 구적법(to1)은 어디까지나 이산적이라는 한계가 존재했다. 구적법이 사용되던 voxel grid 방식과는 차별화된 연속함수라는 점을 NeRF 의 컨트리뷰션으로 본다(from1). NeRF 가 재미있는 점은 구적법을 사용하면서도 구간을 랜덤하게 잡음으로써 (구간에 랜덤한 노이즈를 추가한다고 볼 수도 있다) 연속함수를 흉내낼 수 있다는 아이디어이다(참고3,5).
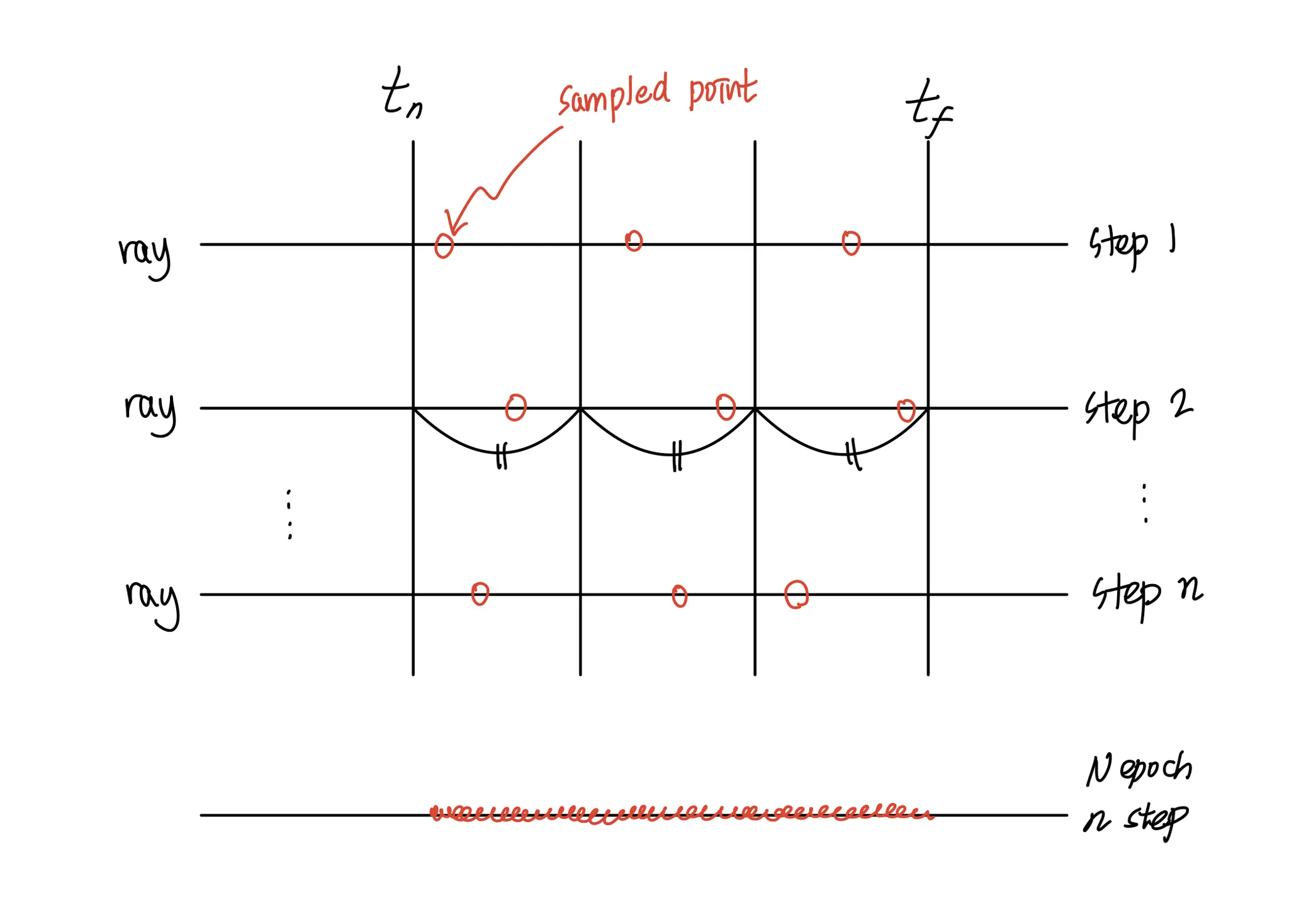
정확히 말하면, Ray 를 하나의 동일한 간격의 구간으로 한번 나눈 뒤, 각 구간에서 균등분포로 한번 더 샘플링을 해 주는 방식을 취했다(참고4). 이러한 방식을 통계학에서는 층화표집( Stratified Sampling) 이라고 한다.
Stratified Sampling) 이라고 한다.
비록 1step 마다 이산적인 샘플들의 집합을 NeRF 에 학습시키지만 층화표집을 통해 step 이 누적될수록 연속적인 3D 공간상의 물체를 표현할 수 있게 될 것이라고 보았다(참고3).
가장 아래의 선에 나타난 붉은색 점들은 학습을 모두 마친 후 네트워크가 마주쳤던 샘플들의 집합이다.
실제로 NeRF 를 구현할 때, 더 정교한 결과물을 얻고 싶으면 에폭수와 스텝수를 늘린다면 더 dense 한 샘플들을 얻게 되고 성능이 높아질 수 있지 않을까 하는 생각이 든다.
from
to
참고
1.
None
2.
None