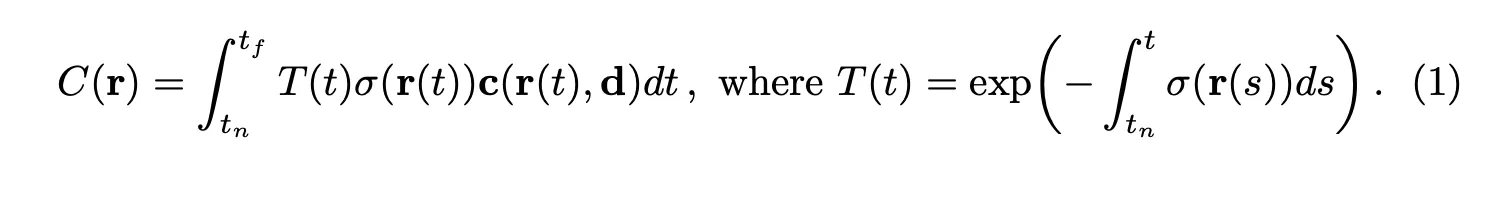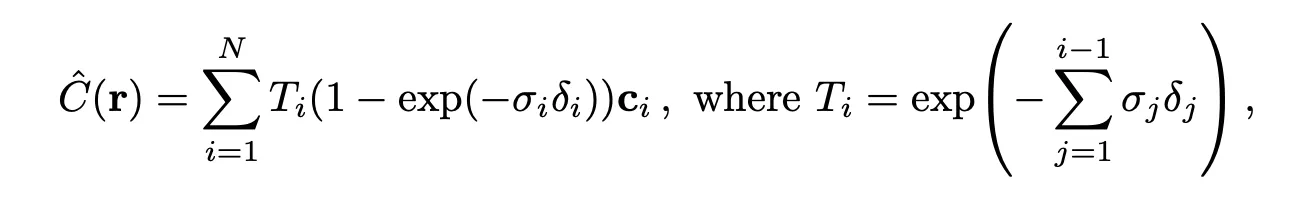🌍

a9.3_4.2. title: 구적법(quadrature)으로 연속이 전제된 Ray 정의식을 이산적으로 표현한다. 이 식은 구적법의 각 구간(delta)길이가 다른 경우에 대해 일반화되어 있다.

생성

🚀 prev note

♻️ prev note

a9.3_4.1. title: NeRF 는 층화표집(‣)으로 연속함수를 표현한다.

🚀 next note

♻️ next note

14 more properties

수식 (참고5)

논문에서는 구적법을 활용해서 위 식을 아래와 같이 다시 정의한다. 고등학교 때 배웠던 구적법과 똑같다.

수식(참고2)

이때

{\delta}_i

는

t_{i+1}-t_i

로 그냥 간격을 의미한다(참고2).

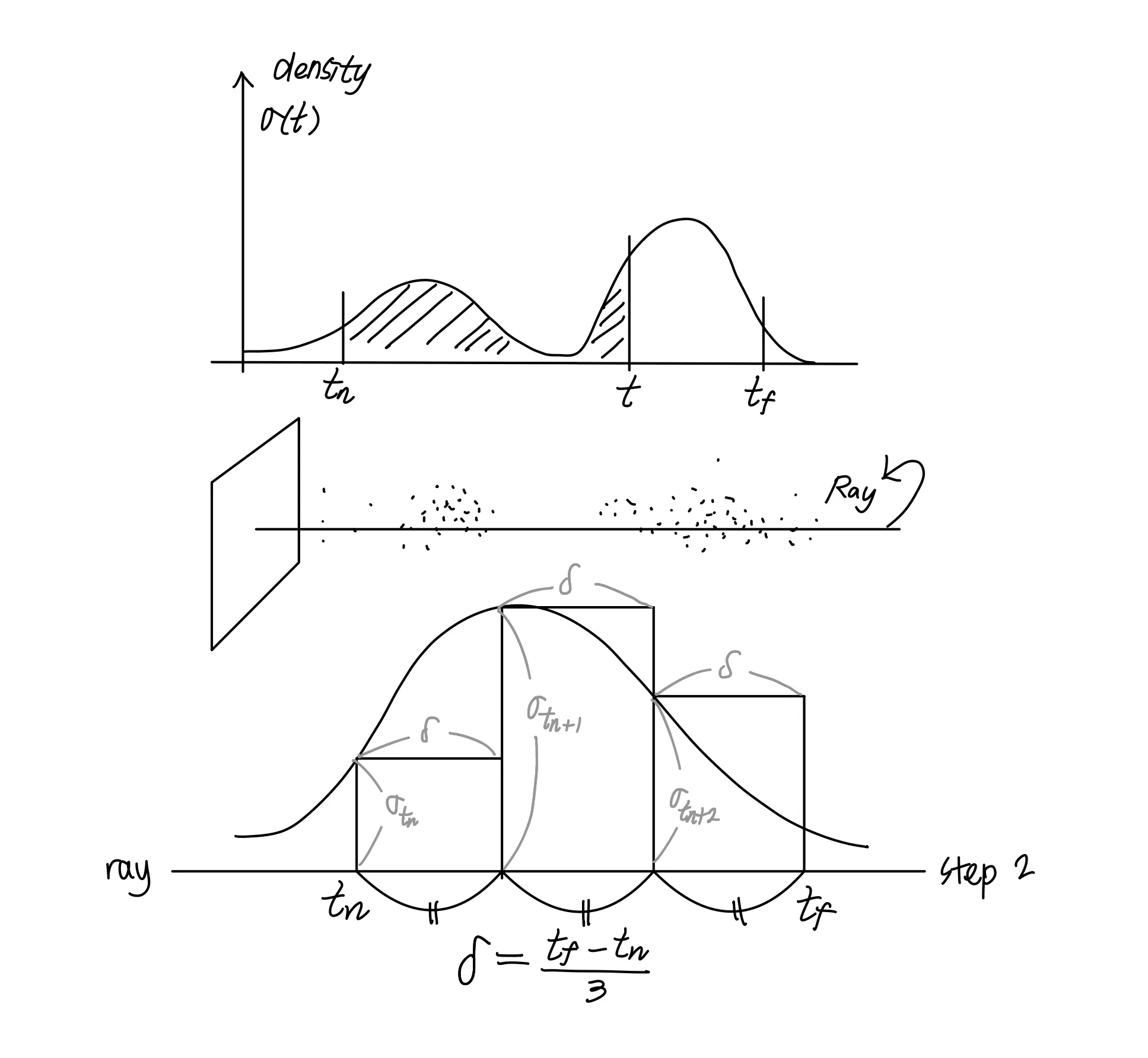
아래 그림은 모든

i

에 대해서

{\delta}

가 동일한 상황이고,

t_{far}

과

t_{near}

사이를 3등분한 결과이다.

위 그림을 이해했다면, 위 수식에서 보이는

{\sigma}{\delta}

가 단순히 구분구적법을 적용하고 있는것임을 알 수 있다.

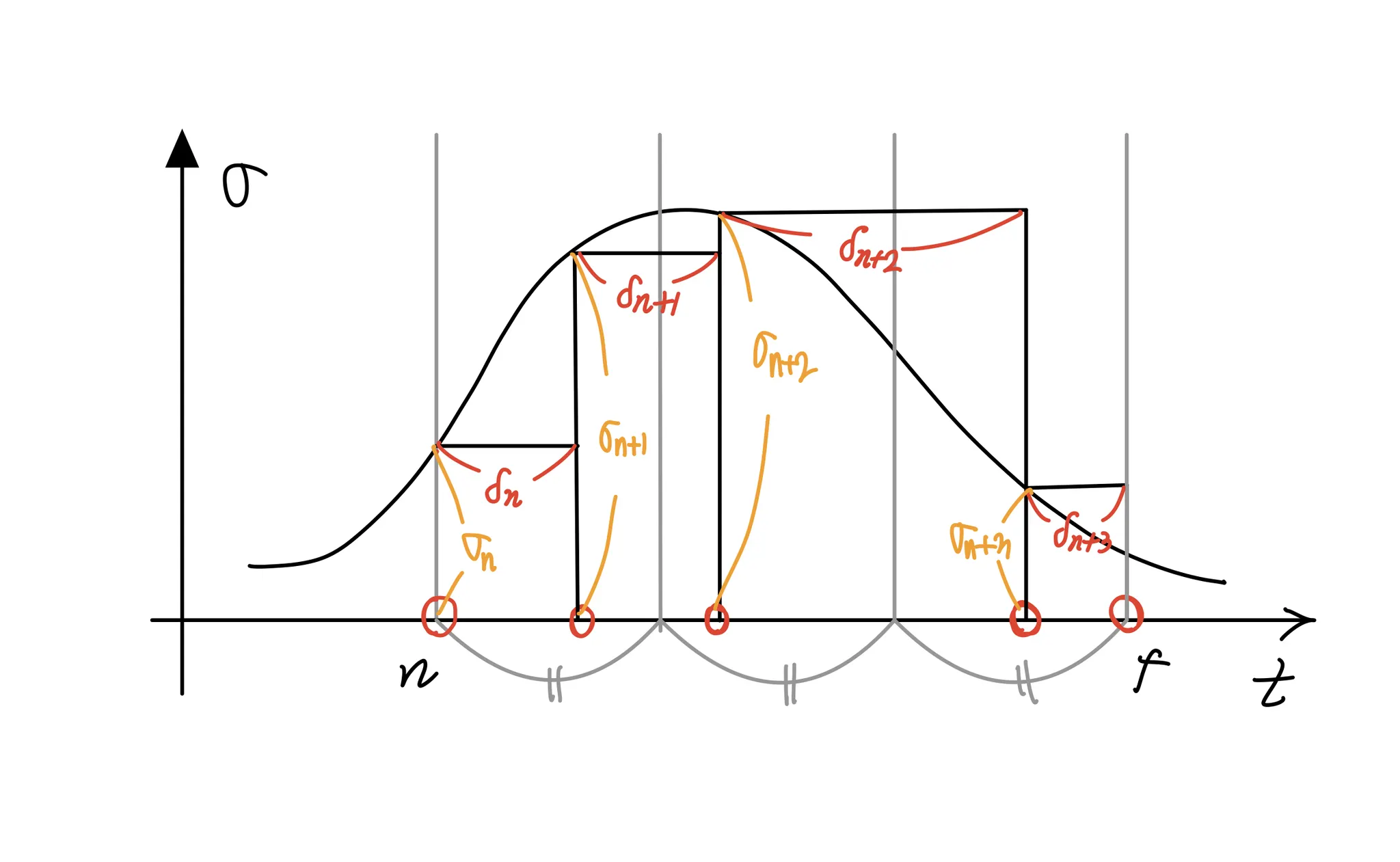
층화표집을 통해 연속함수를 구현했다면(from1), 모든

i

에 대해서

{\delta}_i

의 크기가 동일하지 않을 것이다. 하지만 원리는 똑같다. 아래 그림을 참고하자.

이렇게 구적법(quadrature)으로 연속이 전제된 Ray 정의식을 이산적으로 표현한다. 이 식은 구적법의 각 구간(delta)길이가 다른 경우에 대해 일반화되어 있다.

voxel grid 와 구적법 사이의 관계

NeRF 에서 말하는 구적법의 한계는 정확히 무엇일까? 말로 깔끔하게 설명하려면 어떻게 해야 할까?

NeRF 논문에서 delta 가 의미하는 것

Ray 의 projection 논리를 프로그램으로 구현하기 위해 자연상수 e 의 제곱꼴을 많이 사용하는데, 그 이유가 연산의 편의성 이외에 또 있는가?

from

a9.3_4.1. title: NeRF 는 층화표집(‣)으로 연속함수를 표현한다.

참고

33:00, Continuous 한 것을 discrete 로 바꿔주기 위해서는 sampling 을 해 주어야 한다. Ray 를 n 등분하고, 1 개의 등분 안에서 다시 random sampling 을 한다. Ray 를 따라서 적분하는 것은 다른 논문에서 가져왔다고 한다.

6p, We use these samples to estimate C(r) with the quadrature rule discussed in the volume rendering review by Max [26], where δi = ti+1 − ti is the distance between adjacent samples.

None

None

5p, Volume Rendering with Radiance Fields, The expected color C(r) of camera ray r(t) = o + td with near and far bounds tn and tf is