Search
🔵

b3.4_5.1_2.1__1. title: 투영행렬(‣) P에서 카메라 내부 파라미터(‣), 외부 파라미터(‣) 및 카메라 원점 좌표를 분리하기 위해 QR 분해(‣) 를 사용한다.

생성
🚀 prev note
♻️ prev note
🚀 next note
♻️ next note
14 more properties
투영행렬(‣ Projection matrix)을 구했다고 끝난 것이 아니다. 이것을 다시 유의미한 행렬 단위로 쪼개 주어야 한다.
P=[KR∣−KRX0]\mathrm{P=[KR|-KRX_0]}
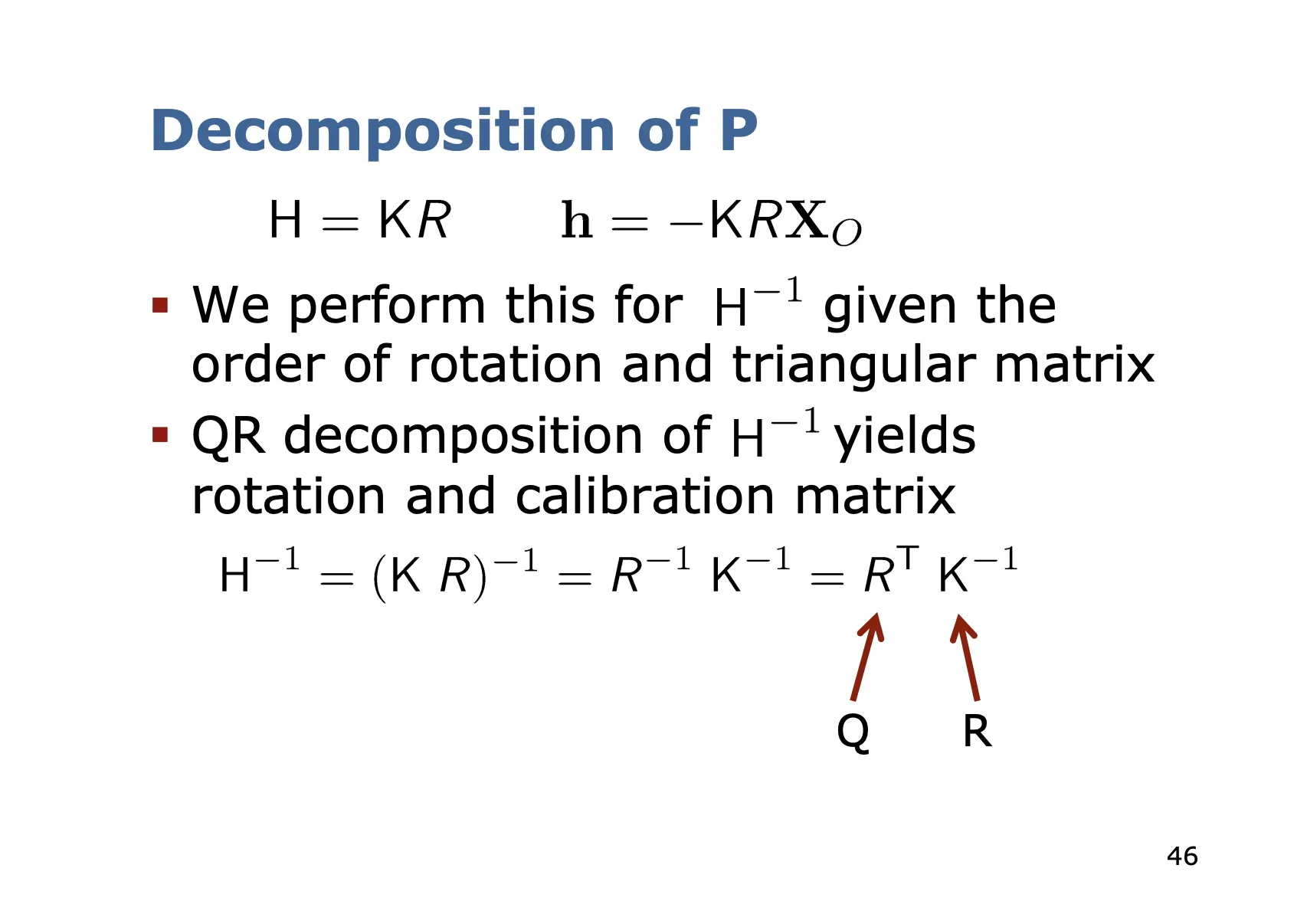
행렬 P\mathrm{P}는 (3,4) 행렬이고, 네 번째 열은 −KRX0\mathrm{-KRX_0}을 나타내는 벡터이다. 따라서, (3,3) 행렬 H=KR\mathrm{H=KR} 로부터 K\mathrm{K} 와 R\mathrm{R} 을 분해해 내는 문제로 수렴한다.
이를 위해 QR 분해(‣ QR decomposition)를 사용한다. QR 분해는 어떤 행렬을 직교행렬과 상삼각 행렬로 분해해 주는 테크닉이다. 카메라 내부 행렬은 상삼각 행렬의 형태를 띠고, 원 혹은 구로부터 유도된 회전 행렬은 직교행렬(‣ Orthogonal matrix (orthonormal set))의 성질을 지닌다.
QR 분해의 결과물은 Q(직교) R(상삼각) 이지, R(상삼각) Q(직교) 가 아니다. 하지만 행렬은 연산의 순서가 중요하다(from1). 순서를 맞추어 주어야 한다. 회전 행렬의 전치행렬은 여전히 직교행렬이고(의문), 카메라 내부 행렬의 역행렬은 여전히 상삼각행렬이다(의문). 따라서 H−1\mathrm{H}^{-1} 을 QR 분해함으로써 회전변환 행렬의 전치행렬과 카메라 내부행렬의 역행렬을 우선 얻어내는 방식으로 회전변환 행렬과 카메라 내부 행렬을 얻어낸다.
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료들.
1.
None
from : 과거의 어떤 생각이 이 생각을 만들었는가?
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는가?
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는가?
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되고 이어지는가?
1.
참고 : 레퍼런스