Search
Duplicate
5️⃣

영역 단위 영상처리 연산과 필터링

•
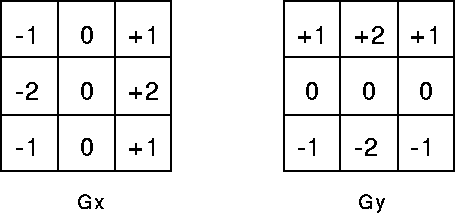
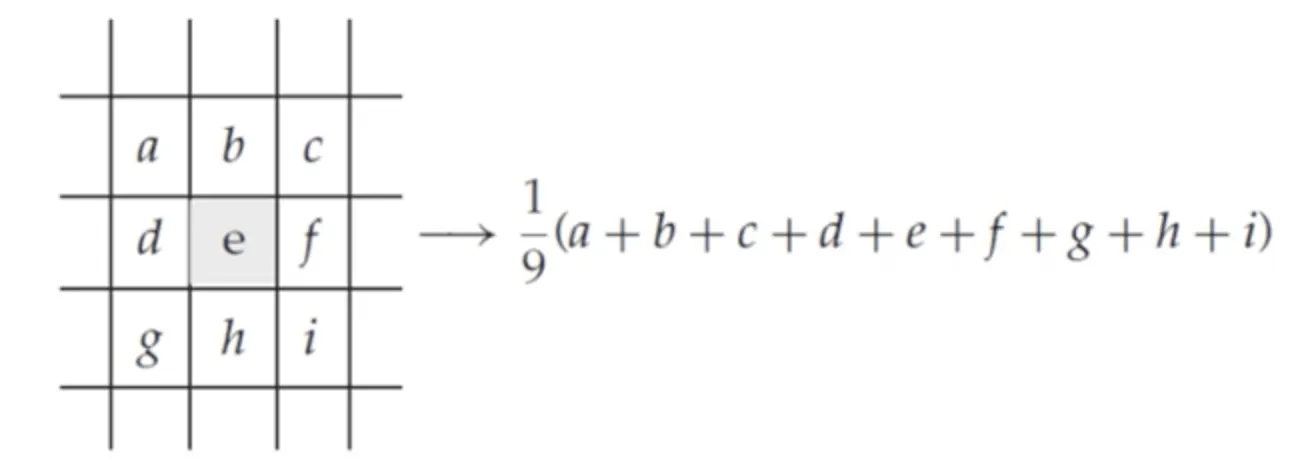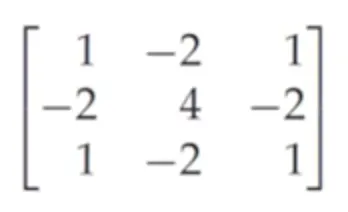2021/02/23~2021/02/26, 2023/10/18~2023/10/20

영상처리 연산

영상의 화소(pixel)값을 변경하는 일을 영상처리 연산이라고 한다.
•
화소 단위 처리: 하나의 화소값만을 사용하여 화소값을 변경
•
영역 단위 처리: 이웃 화소들을 참조하여 화소값을 변경
•
영상 단위 처리: 기하적 변환(Transform)

영역 단위 처리

영역 단위 처리는 화소 단위 처리의 확장으로, 주어진 화소의 이웃한 화소에 대해서도 함수를 적용하는 것을 의미한다.
•
영역 단위 처리에서 자주 나오는 개념들
◦
마스크
▪
마스크를 주어진 영상 위로 이동하면서 처리한다.
▪
마스크는 일반적으로 양변의 길이가 홀수인 사각형이지만, 다른 형태도 가능하다.
◦
필터
▪
마스크와 함수를 결합한 것을 필터(filter)라고 한다.
▪
필터에 적용된 함수가 선형이면 선형 필터, 아니면 비선형 필터라고 한다.

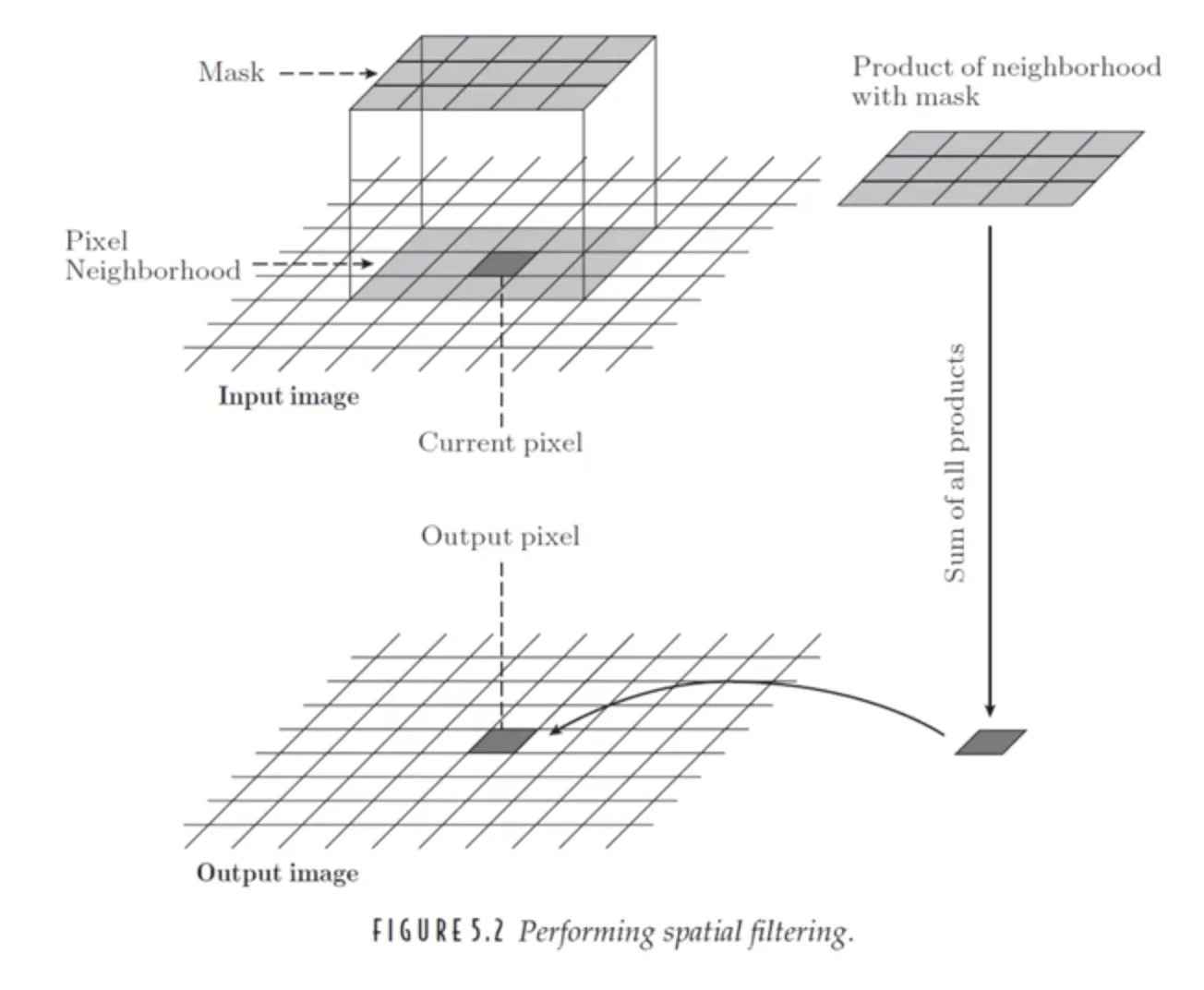
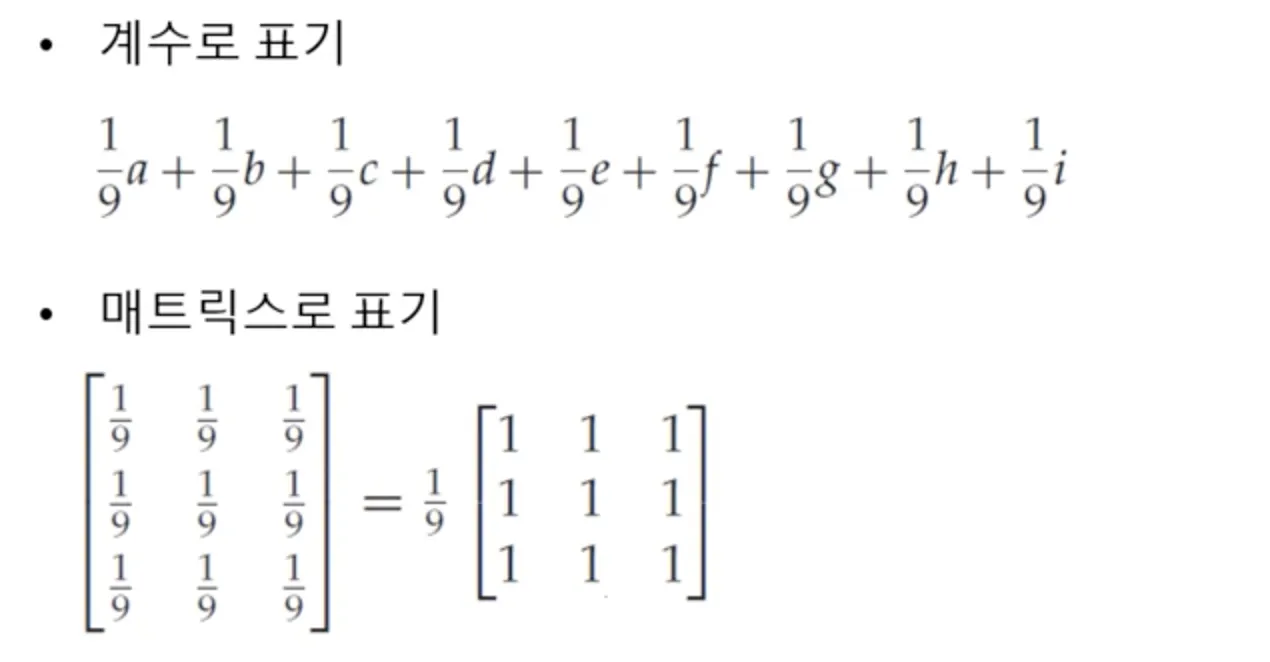
공간 필터링(spatial filtering)

선형 필터(비선형 필터 말고)는 마스크 내의 모든 원소와 이에 대응하는 이웃 영역에 있는 모든 화소들의 값들에 임의의 곱셈 연산을 적용하고 이들을 모두 더하여 구현된다. 이를 공간 필터링(spatial filtering)이라고 한다.
dst(x,y)=∑i=−11∑j=−11m(i,j)src(x+i,y+j)dst(x, y)=\sum_{i=-1}^{1}\sum_{j=-1}^{1}{m(i,j)src(x+i, y+j)}
•
m(s,t)m(s,t) 는 마스크 특정 위치의 픽셀 강도를 의미한다.
•
p(i+s,j+t)p(i+s, j+t) 는 원본 이미지 특정 위치의 픽셀 강도를 의미한다.
필터의 영역에서 가장 큰 값을 찾아내는 필터(비선형 필터)가 있다고 해 보자. 이런 경우에는 위의 식과 같이 시그마가 필요없을지도 모른다. 뉴럴 네트워크에서는 중간중간 최댓값 풀링 레이어들이 존재한다. 이런 레이어의 존재 이유를 설명할 때 비선형성이라는 용어가 등장한다.

공간 회선(spatial convolution)

마스크 또는 이미지를 180도 회전시킨다는 점을 제외하고, 공간 필터링과 작동 방식이 완전히 동일하다. 이를 식으로 작성하면 다음과 같다.
•
마스크 회전
dst(x,y)=∑i=−11∑j=−11m(−i,−j)src(x+i,y+j)dst(x, y)=\sum_{i=-1}^{1}\sum_{j=-1}^{1}{m(-i,-j)src(x+i, y+j)}
•
영상 회전
dst(x,y)=∑i=−11∑j=−11m(i,j)src(x−i,y−j)dst(x, y)=\sum_{i=-1}^{1}\sum_{j=-1}^{1}{m(i,j)src(x-i, y-j)}

공간 필터링 vs 공간 회선

나는 그냥 공간 필터링과 공간 회선(convolution)이 완전히 동일한 연산인줄 알았다. 엄밀히 따지면 이것은 오개념이다. 사람들이 굳이 영상처리에 있어 필터링과 회선을 이미지에 대해서 구분하지 않았던 이유는, 마스크가 회전에 대해서 대칭이기 때문이다. 딥러닝을 이용한 영상처리에서도 수많은 필터들이 180도 돌려서 계산되든 말든, 학습에 의해 결정되고 마스크의 형태가 중요하지 않기 때문에 굳이 둘을 구분할 필요가 없었던 것이다.

필터

•
필터
•
표기법

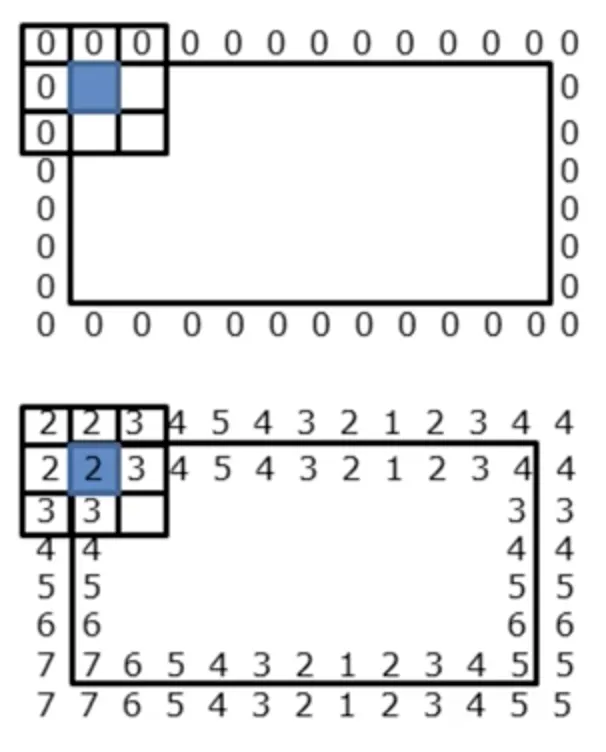
영상 필터링의 모서리(edge) 처리

위: 제로패딩, 아래: 미러링
•
무시하기: 필터링 결과 영상의 크기가 원본보다 작아짐.
•
미러링(mirroring, reflect): OpenCV 기본값
def mirroring(x, pad=1): for i in range(pad): x = np.concatenate([x[0,None], x, x[-1,None]], axis=0) x = np.concatenate([x[:,[0]], x, x[:,[-1]]], axis=1) return x mirroring(np.array([[1,2,3], [4,5,6], [7,8,9]]), 2)
Python
복사
미러링 구현
•
제로패딩(zero padding): 영상의 테두리에서는 원하지 않는 결과가 나타날 수 있다.
def zero_padding(x, pad=1): for i in range(pad): row = x.shape[0] col = x.shape[1] pad_col = np.zeros([1, col]) x = np.concatenate([pad_col, x, pad_col], axis=0) pad_row = np.zeros([row+2, 1]) x = np.concatenate([pad_row, x, pad_row], axis=1) return x zero_padding(np.array([[1,2,3], [4,5,6], [7,8,9]]), 2)
Python
복사
제로패딩 구현
모서리에 주목

주파수 통과 필터

•
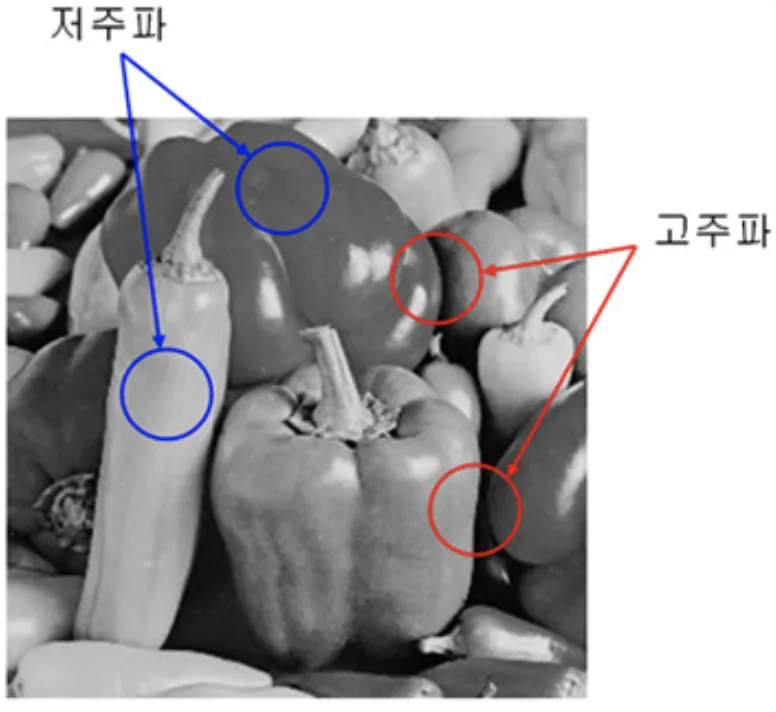
일반적으로 주파수라고 함은, 시간축에 대해서 어떠한 값이 진동하는 횟수이다.
•
하지만 당연히 단일 영상에는 시간축이 존재하지 않는다.
•
따라서, 고주파와 저주파를 다음과 같이 정의한다.
◦
고주파: 짧은 거리 내에서 밝기변화가 매우 큰 성분
▪
영상의 모소리, 울퉁불퉁
◦
저주파: 밝기값이 거의 변하지 않는 성분
▪
피부, 단색의 벽
•
이런 고주파와 저주파를 통과시키는 필터들이 있다.
◦
저주파를 줄이거나 제거하며 고주파를 통과시키는 필터: 고역 통과 필터
◦
고주파를 줄이거나 제거하며 저주파를 통과시키는 필터: 저역 통과 필터
고역 통과 필터
저역 통과 필터
•
고역 통과와 저역 통과에 대해서는 영상 도메인이 아니라 주파수 도메인에서 처리하곤 한다.
•
고역 통과 필터를 거치면 다음과 같은 결과물을 얻을 수 있다.
◦
라플라시안 필터, 소벨 필터 등이 이에 속한다.
•
저역 통과 필터를 거치면 다음과 같은 결과물을 얻을 수 있다.
◦
가우시안 필터 등이 이에 속한다.

저역 통과 필터

•
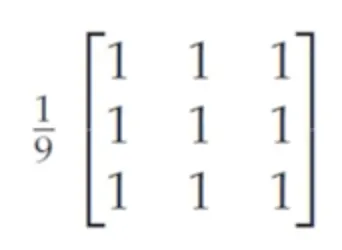
저역 통과 필터는 블러(blur) 필터라고도 불린다.
◦
가우시안(gaussian) 필터, 평균(mean) 필터가 대표적인 저역 통과 필터이다.
•
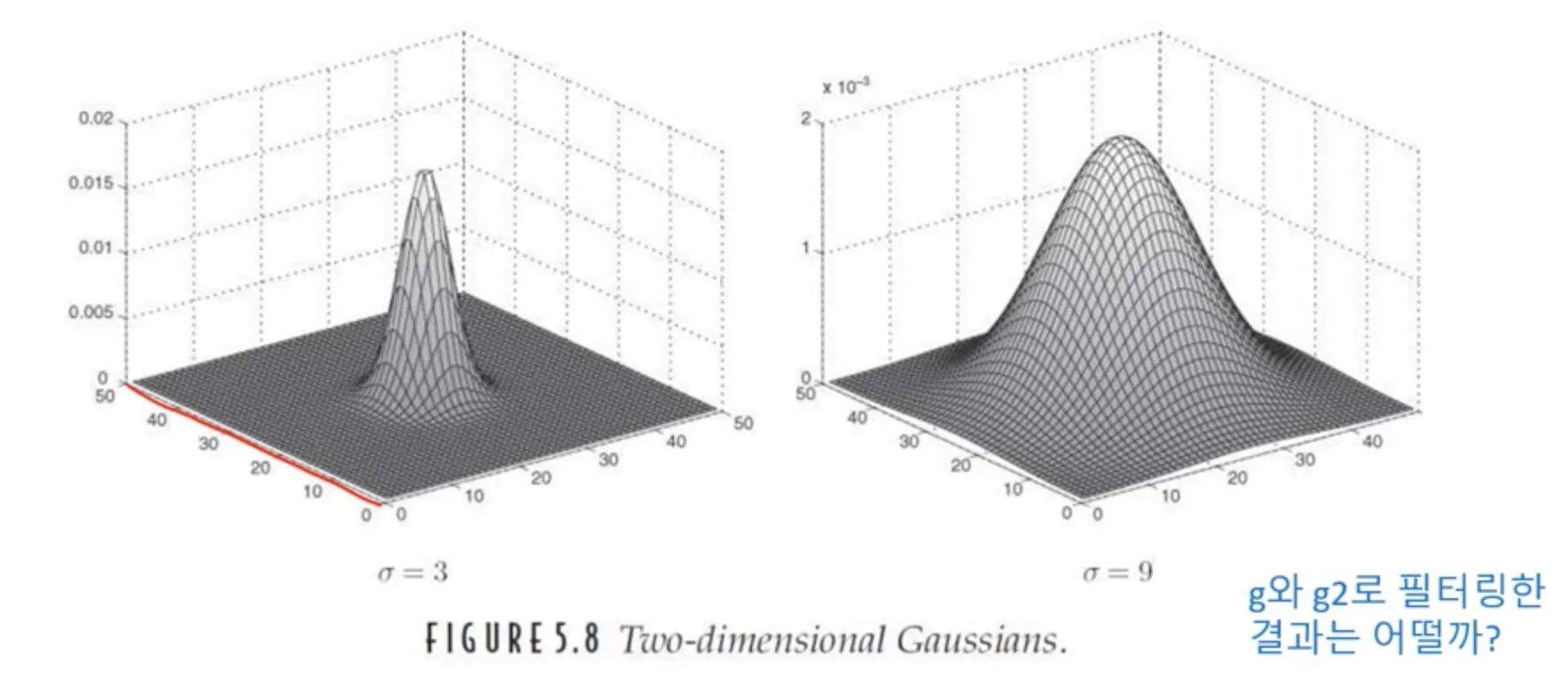
가우시안 필터
1차원 데이터에 적용하는 가우시안 필터
2차원 데이터(영상 등)에 적용하는 가우시안 필터
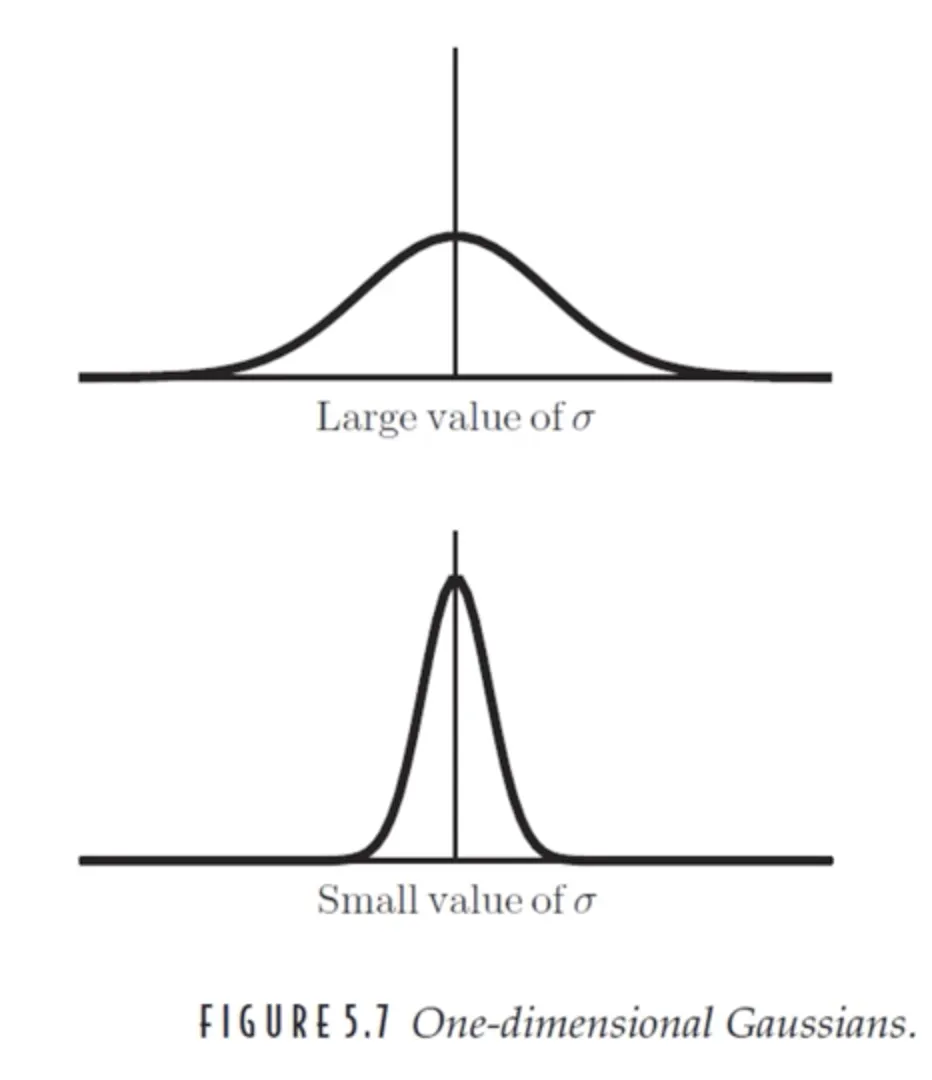
좌
우
표준편차
작다
크다
결과
필터가 올라간 영상의 영역 중심에만 큰 가중치가 곱해진다. 따라서 원본 영상과 비슷한 결과를 얻을 수 있다.
필터가 올라간 영상 영역을 중심으로 서서히 가중치가 곱해지므로 원본 영상이 블러링되는 정도가 클 것이다.
가우시안 필터의 표준편차 변화와 필터 크기의 변화에 따른 결과값 비교
가우시안 필터의 특징을 이용해 복잡한 연산을 수행하기도 한다.
•
가우시안의 푸리에변환은 가우시안이다.
•
가우시안은 회전에 대해서 대칭이다.
•
가우시안 필터는 분리가능하다.
•
두 개의 가우시안 필터의 회선(convolution)은 또다른 가우시안이다.

에지 샤프닝(edge sharpening)

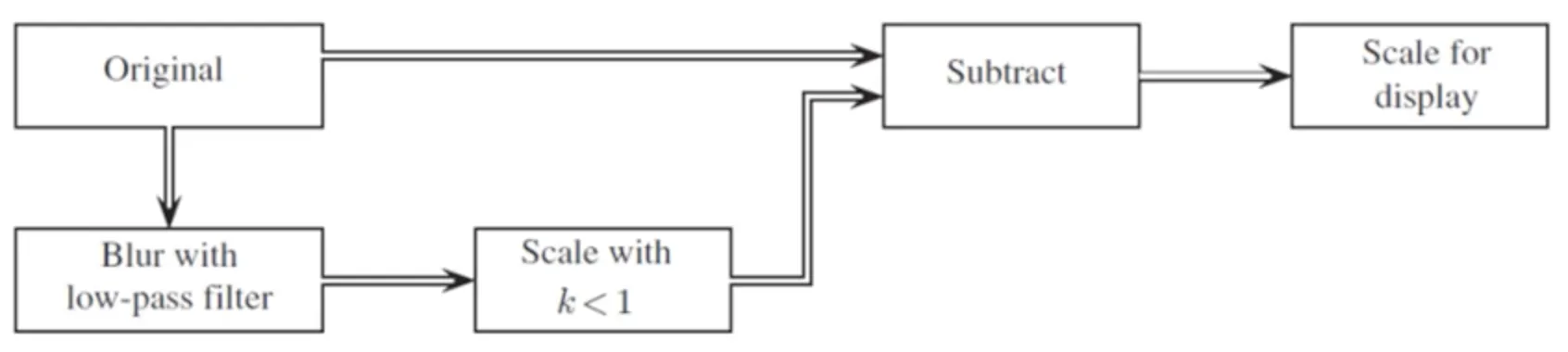
공간 필터링을 통해 영상의 에지를 더욱 날카롭고 선명하게 만드는 것을 에지 샤프닝(edge sharpening)이라고 한다. 이러한 연산은 엣지 강조(edge enhancement), 엣지 선명(edge crispening), 언샤프 마스킹, 언샤프 마스크 필터링(unsharp mask filtering, 인쇄 산업에서 주로 사용하는 용어)이라고도 불린다.
저역 통과 필터를 이용한 에지 샤프닝 파이프라인
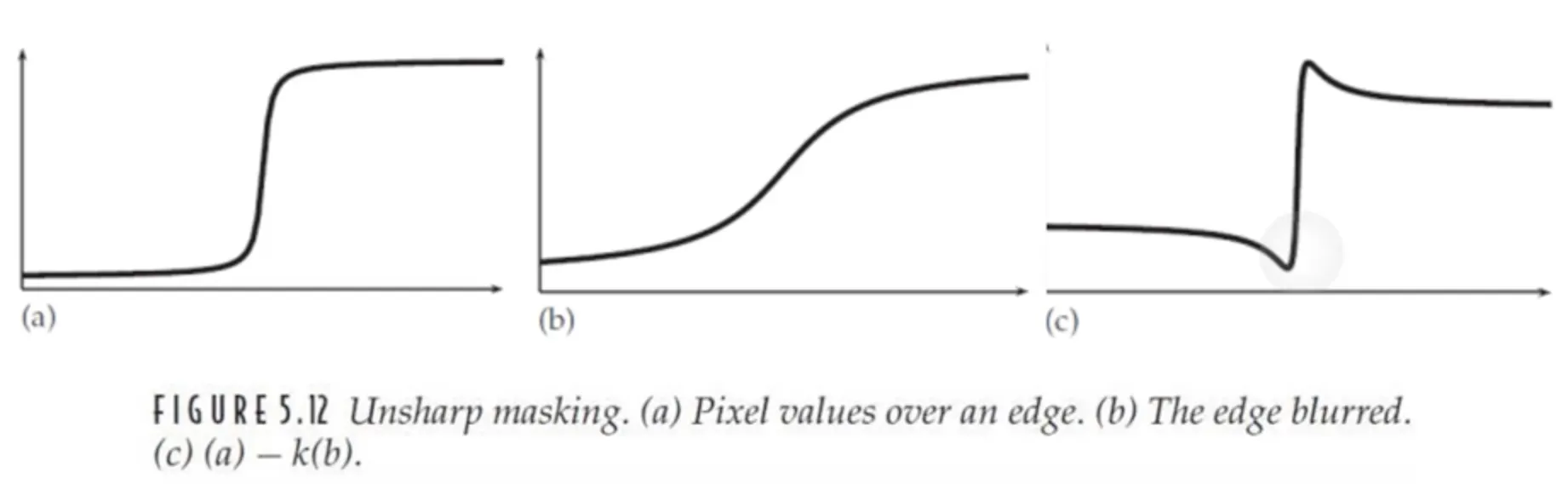
픽셀 강도의 변화가 시작되는 부분과, 끝나는 부분을 잘 나누어 생각해 보자.
•
의미를 이해해 보자.
◦
원본 영상(a)의 저역 통과 필터를 거친 영상(b)를 원본 영상에서 빼 주면
◦
저주파 성분이 제거된 영상을 얻을 수 있다.
◦
저주파 성분이 제거된 결과물을 원본 영상(a)에 더하면 고주파가 강조된 결과물(c)을 얻을 수 있다.

선형 필터 연산 결과의 픽셀 강도 범위 초과

•
영상으로 만들기 위해서는 값이 [0, 255] 범위에 있어야 한다.
•
하지만 선형필터(비선형이 아닌)를 사용한다면 y=kxy = kx 의 꼴로 연산이 일어나기 때문에, 필터링 결과 픽셀의 픽셀 강도가 영상의 픽셀 강도 표현범위 [0, 255]를 벗어날 수 있다.
•
해결 방법은 다음과 같다.
1.
음수를 양수로 바꾸기
•
절댓값 등을 사용한다.
•
음수 문제를 해결할 수 있지만, 255보다 큰 값을 처리할 수 없다.
2.
값의 제한
•
음수와 양수 문제 모두를 해결할 수 있다.
•
[0, 255] 의 범위를 벗어나는 결과물이 많은 경우, 정보의 손실이 매우 커진다.
3.
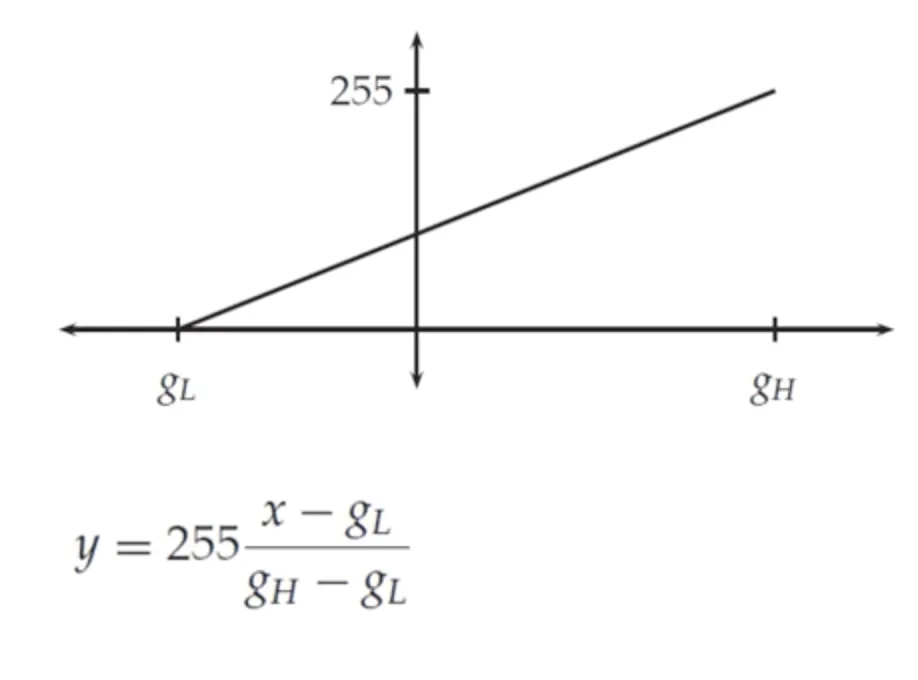
스케일링
•
가장 무난한 방법이다.
•
필터링 결과의 최소값이 gLgL, 가장 큰 값이 gHgH 라고 할 때 gL=0gL = 0 이고, gH=255gH = 255 가 되도록 선형변환을 수행하는 방법이다.

적응형 필터(adaptive filter)

적응형 필터는 마스크 내의 픽셀 강도에 따라 필터가 달라지는 필터를 의미한다.

양방향 필터(bilateral filter)

•
적응형 필터 중 하나로 가우시안 필터의 단점을 보완한다.
가우시안 필터를 사용하는 경우 필터(그림에서 kernel)의 형상은 항상 동일하다.
◦
적응형 필터이기 때문에 필터가 상황에 맞게 변화한다.
양방향 필터를 사용하면 에지에서 필터가 변화하여 가우시안 필터가 적용되지 않는다.
•
유도
◦
가우시안 필터는 아래와 같이 표현할 수 있다.
GFσ(I,(x,y))=1W∑q∈Sfσ((x−xq)2+(y−yq)2)I(x,y)GF_{\sigma}(I, (x,y)) =\frac{1}{W} \sum_{q\in{S}} { f_{\sigma} (\sqrt{(x-x_q)^2+(y-y_q)^2})I(x,y) }
GFGF
가우시안 필터 함수
II
영상
(x,y)(x,y)
가우시안 필터를 적용할 위치
ff
정규분포 함수
σ\sigma
정규분포의 표준편차
WW
필터 합이 1이 되도록 만드는 정규화 상수
◦
이를 벡터 표기를 이용해 조금 더 단순히 표현하면 다음과 같다.
GF[I]p=1Wp∑q∈SGσ(∣∣p−q∣∣)IqGF[I]_\textbf{p}=\frac{1}{W_\textbf{p}} \sum_{\textbf{q}\in{S}} { G_{\sigma} (||\textbf{p}-\textbf{q}||) I_\textbf{q} }
◦
양방향 필터는 이 가우시안 필터에 에지 필터를 곱셈으로 결합한 형태일 뿐이다.
▪
우리가 상상하는 에지 필터는 보통 다음과 같은 모습이다.
▪
앞서 GF[I]pGF[I]_p 식과 최대한 비슷한 형태로 에지 필터를 표현하면 다음과 같다.
E[I]p=1Wp∑q∈SGσ(∣Ip−Iq∣)IqE[I]_\textbf{p}=\frac{1}{W_\textbf{p}} \sum_{\textbf{q}\in{S}} { G_{\sigma} (|I_\textbf{p}-I_\textbf{q}|) I_\textbf{q} }
[2,1,0,−1,−2][2, 1, 0, -1, -2]로 구성된 필터는 의미적으로 아래 그림과 같이 [1,0,−1][1, 0, -1]로 구성된 필터에 가우시안을 적용한 것이다.
따라서 에지 필터의 역할만 수행할 수 있다면, E[I]p E[I]_\textbf{p}식에서 Gσ(∣Ip−Iq∣)G_{\sigma} (|I_\textbf{p}-I_\textbf{q}|) 을 사용하든, Gσ(∣∣Ip−Iq∣∣)G_{\sigma} (||I_\textbf{p}-I_\textbf{q}||) 을 사용하든, ∣Ip−Iq∣|I_\textbf{p}-I_\textbf{q}| 을 사용하든 관계가 없다. 하지만 일반적으로 Gσ(∣Ip−Iq∣)G_{\sigma} (|I_\textbf{p}-I_\textbf{q}|) 을 사용하므로 이것을 채택한다.
◦
둘을 결합하면 다음과 같다.
BF[I]p=1Wp∑q∈SGσ(∣∣p−q∣∣)Gσ(∣Ip−Iq∣)IqBF[I]_p = \frac{1}{W_\textbf{p}} \sum_{\textbf{q}\in{S}} { G_{\sigma} (||\textbf{p}-\textbf{q}||) } G_{\sigma} (|I_\textbf{p}-I_\textbf{q}|) I_\textbf{q}
당연히 양방향 필터도 만능의 도구는 아니다. 이 필터는 에지가 잡음보다 강한 경계를 가질 것이라는 점을 전제하고 있다.

비선형 필터(nonlinear filter)

비선형 필터는 마스크 내의 픽셀 강도에 비선형 함수를 적용한다.
•
순위 필터(rank-order filter): 필터 내의 밝기값들을 정렬하고, 이에서 미리 정해진 n 번째 값을 취하는 필터. 정렬이 필요하기 때문에 매우 느리다는 특징이 있다.
◦
최댓값 필터
◦
최솟값 필터
◦
중간값 필터(median filter)
▪
마스크에 포함된 픽셀 강도의 중간값(median)을 사용한다.
▪
마스크가 포함하는 픽셀이 짝수개라면 중앙 두 값의 평균값을 쓴다.

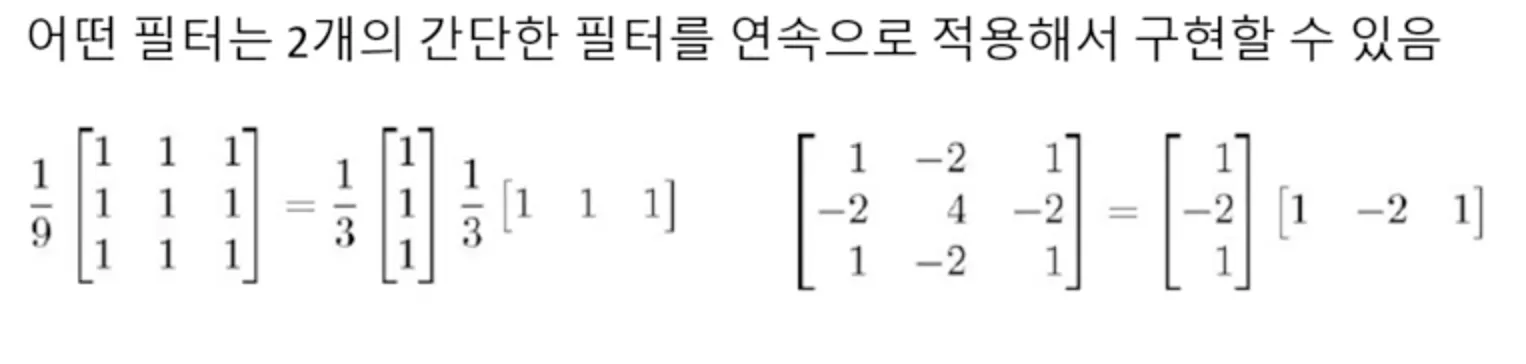
분리가능한 필터(separable filter)

필터의 크기
5x5
5x1 → 1x5
연산량
25wh25wh
5wh+5wh5wh+5wh
MobileNet(2017)등에서 제안한 Depthwise Separable Convolution 같은 것들도 결국 이런 영상처리의 최적화 아이디어를 뉴럴 네트워크에 적용한 것이다.