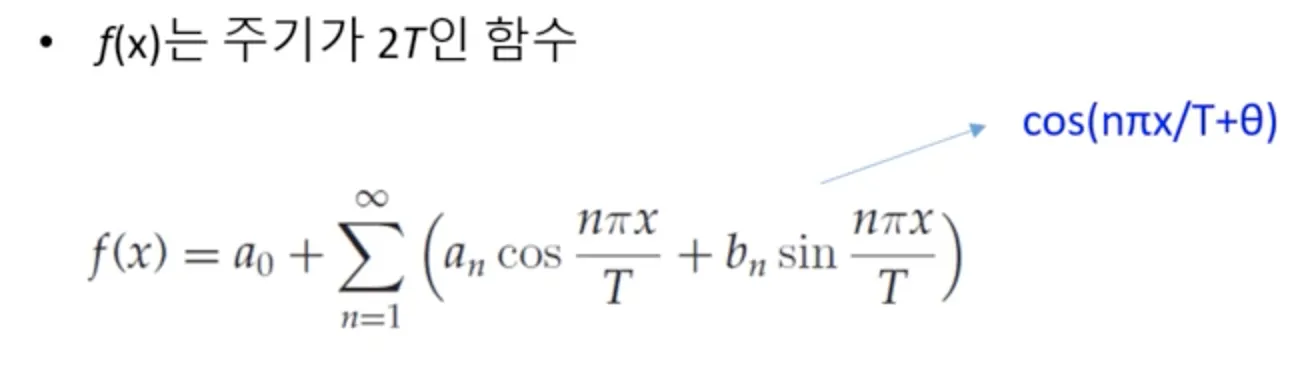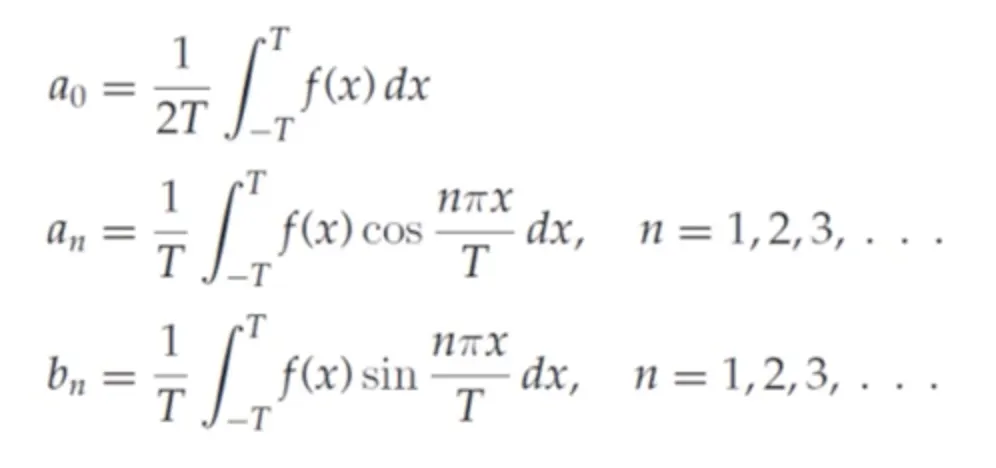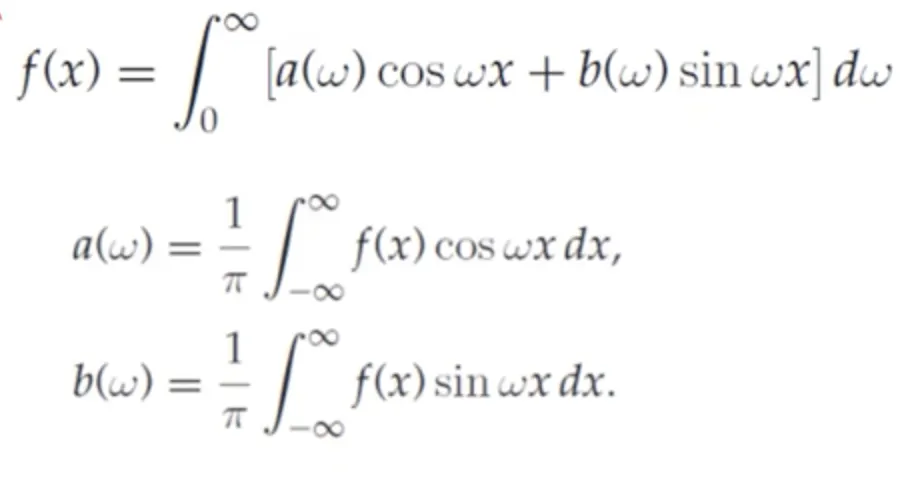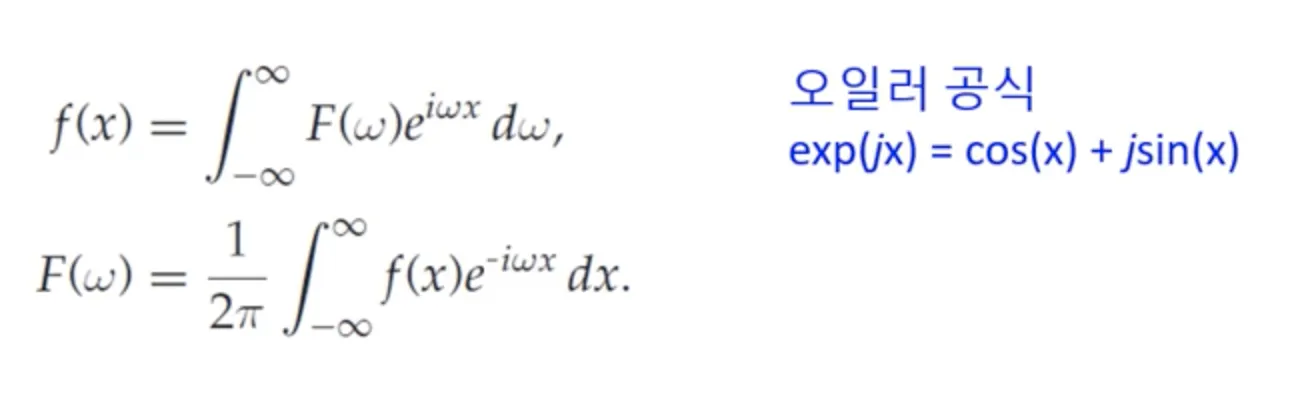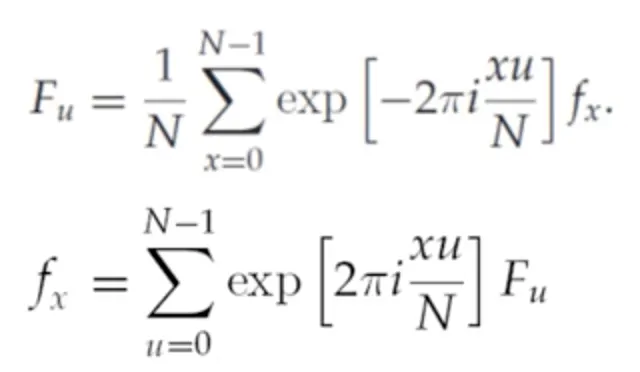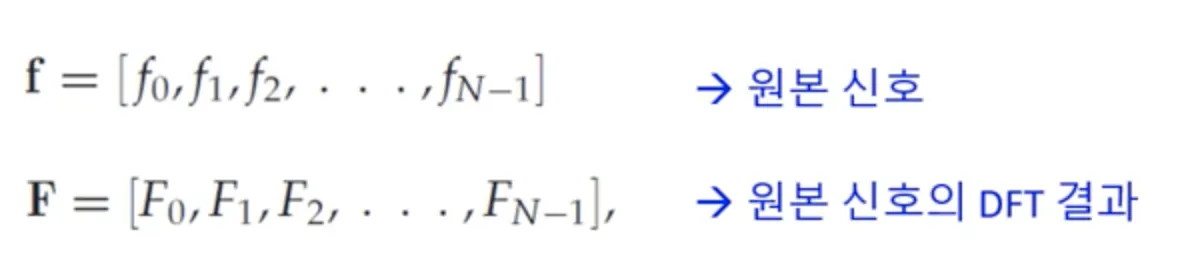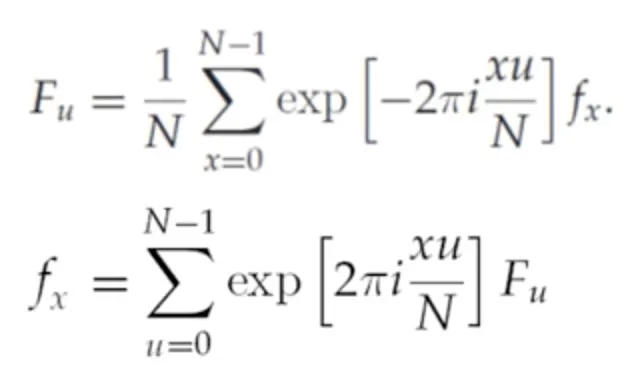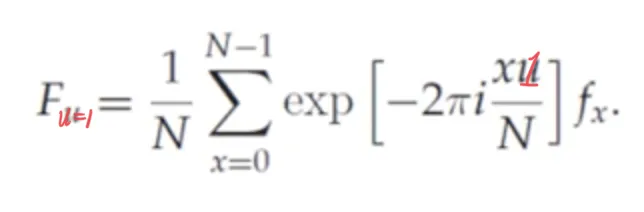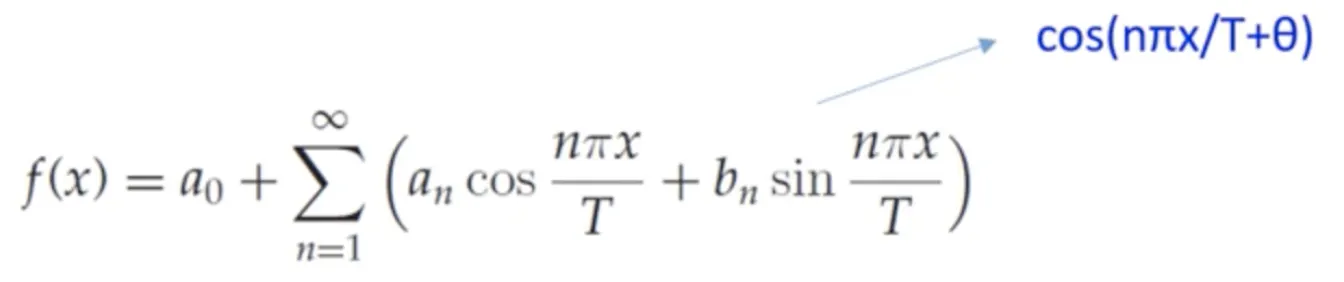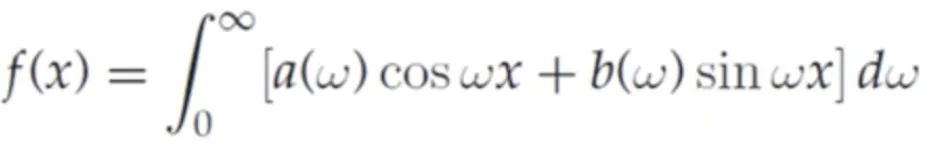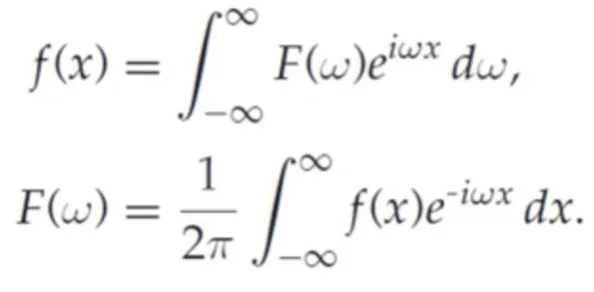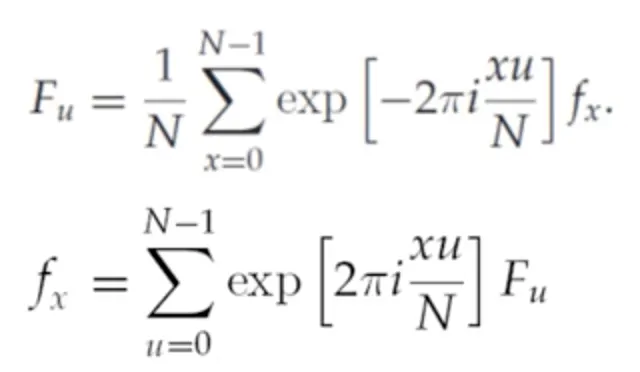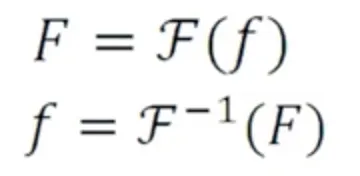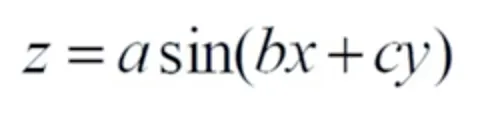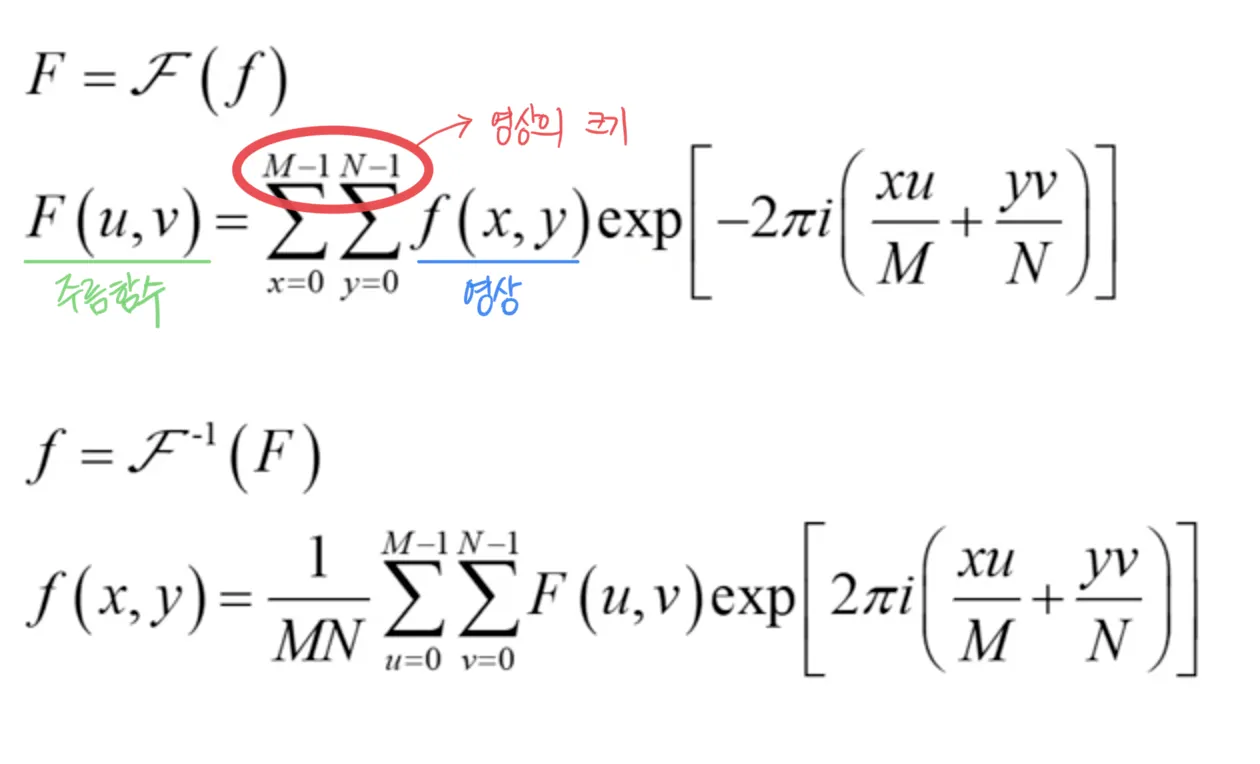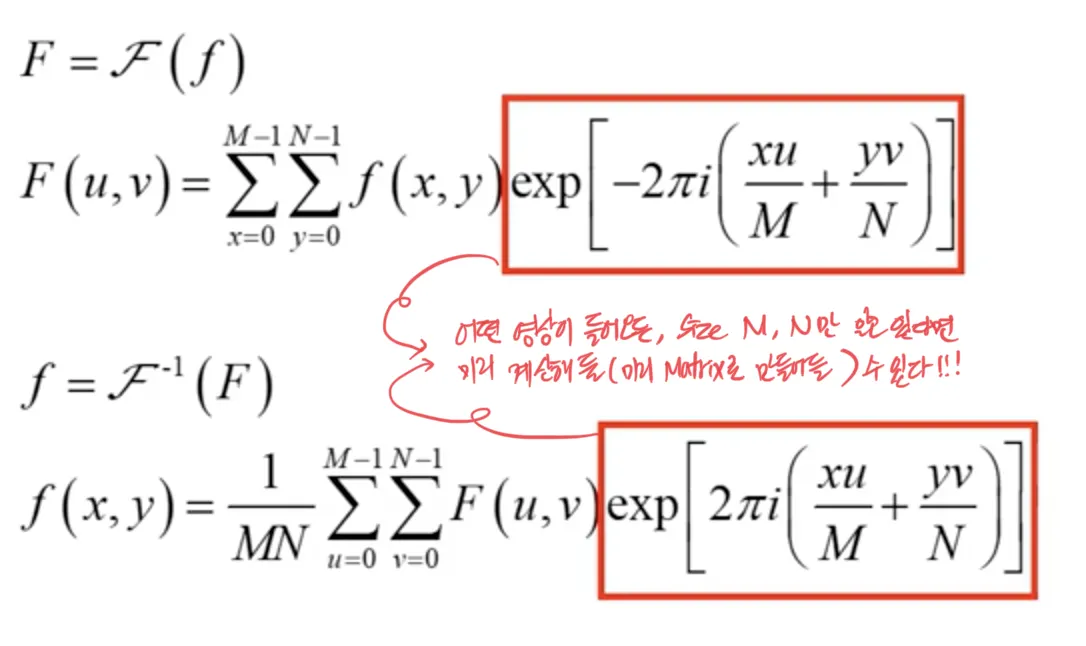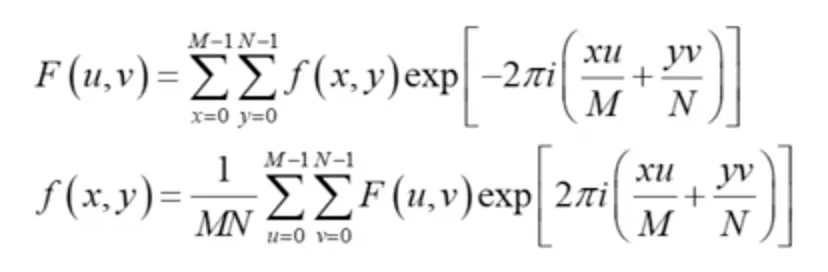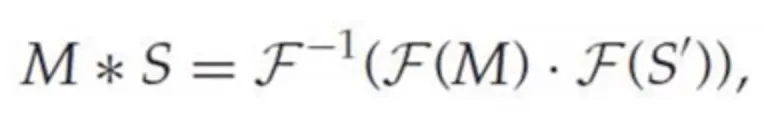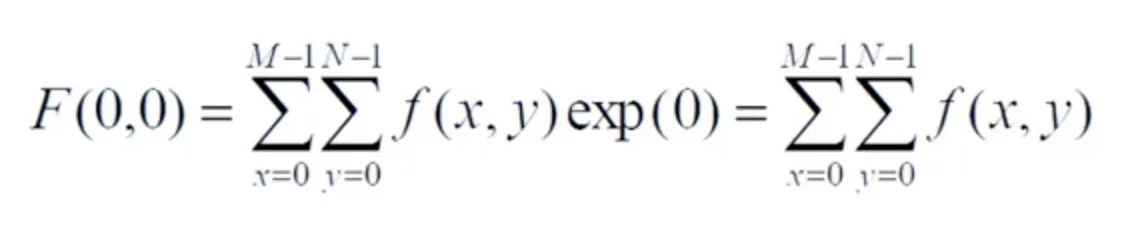들어가기 전에
공부할 때 주의사항
영상을 공간 도메인이 아니라, 주파수 도메인에서 분석하는 것을 배우게 된다. 대부분의 수식들은 신호처리 관점에서 나온 아이디어이고, 영상처리를 살펴볼 때에는 컨셉적인 측면을 위주로 이해해야 한다.
주파수 영역 처리의 과거와 미래
예전에는 주파수 도메인에서 영상처리를 하는 일들을 굉장히 많이 했었다. 요즘은 예전만큼 사용하지는 않는다. 어쨌든, 영상처리에서 매우 중요한 역할을 했다. 요즘은 이 부분의 중요성이 굉장히 크지는 않지만, 알아둘 필요는 분명히 있다.
주파수 영역 해석의 장점
•
영상의 특정 주파수성분을 정밀하게 분리하고 처리할 수 있게 된다.
•
•
영상에 적게 포함된 주파수성분을 제거하여, 영상의 용량을 줄일 수 있도록 도와준다.
배경 지식 : 푸리에 급수 (Fourier series)
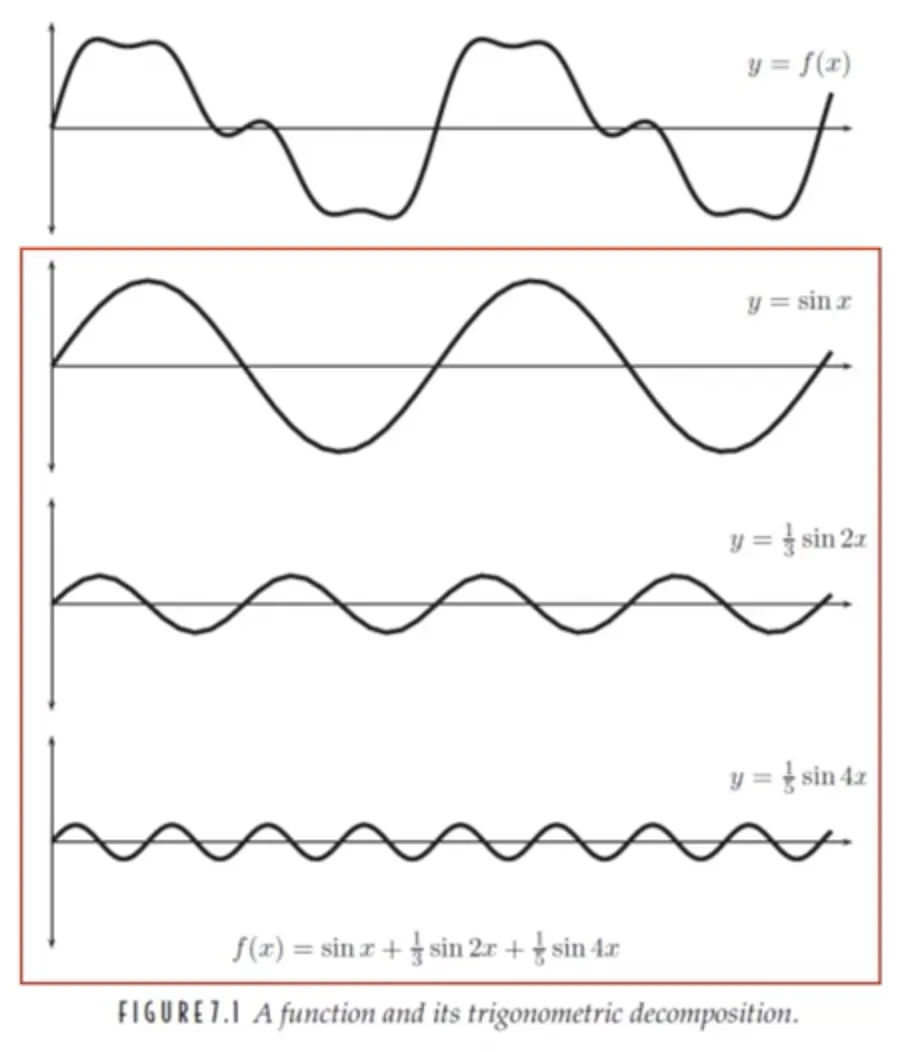
푸리에 급수는 임의의 비주기함수를 삼각함수들의 조합으로 표현하는 것을 의미한다.
즉, 주기함수는 진폭과 주파수가 다른 사인파와 코사인파의 합으로 표현할 수 있다.
의미적 설명
함수와 함수는 모두 주기가 이고, 의 주기는 이다.
따라서 의 주기는 이다.
최소주기는 이 되겠지만, 결국 주기는 이다. ( 이 커지더라도)
: n 번째 cos 신호의 강도 (진폭)
: n 번째 sin 신호의 강도 (진폭)
: y 축 평행이동
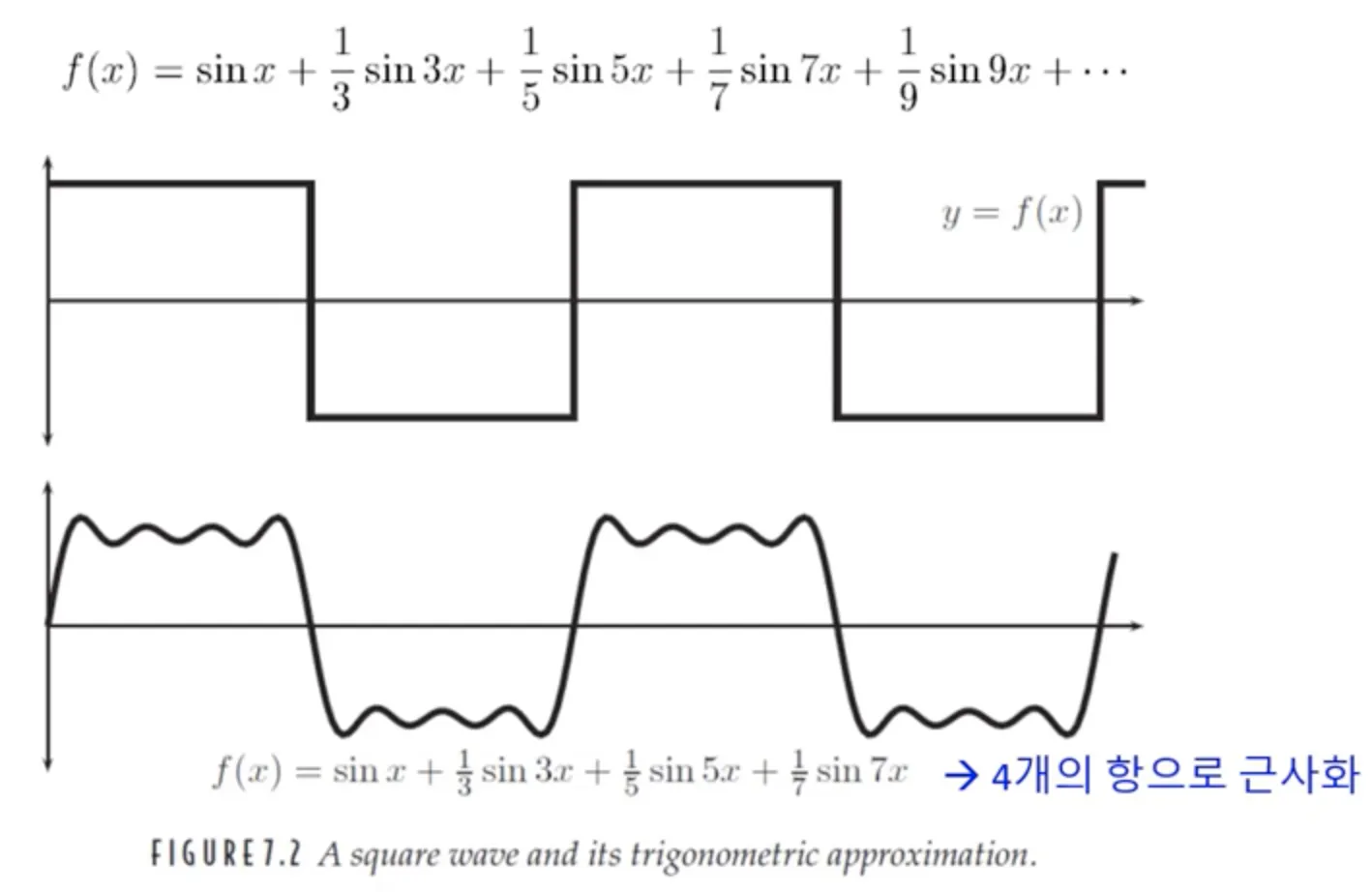
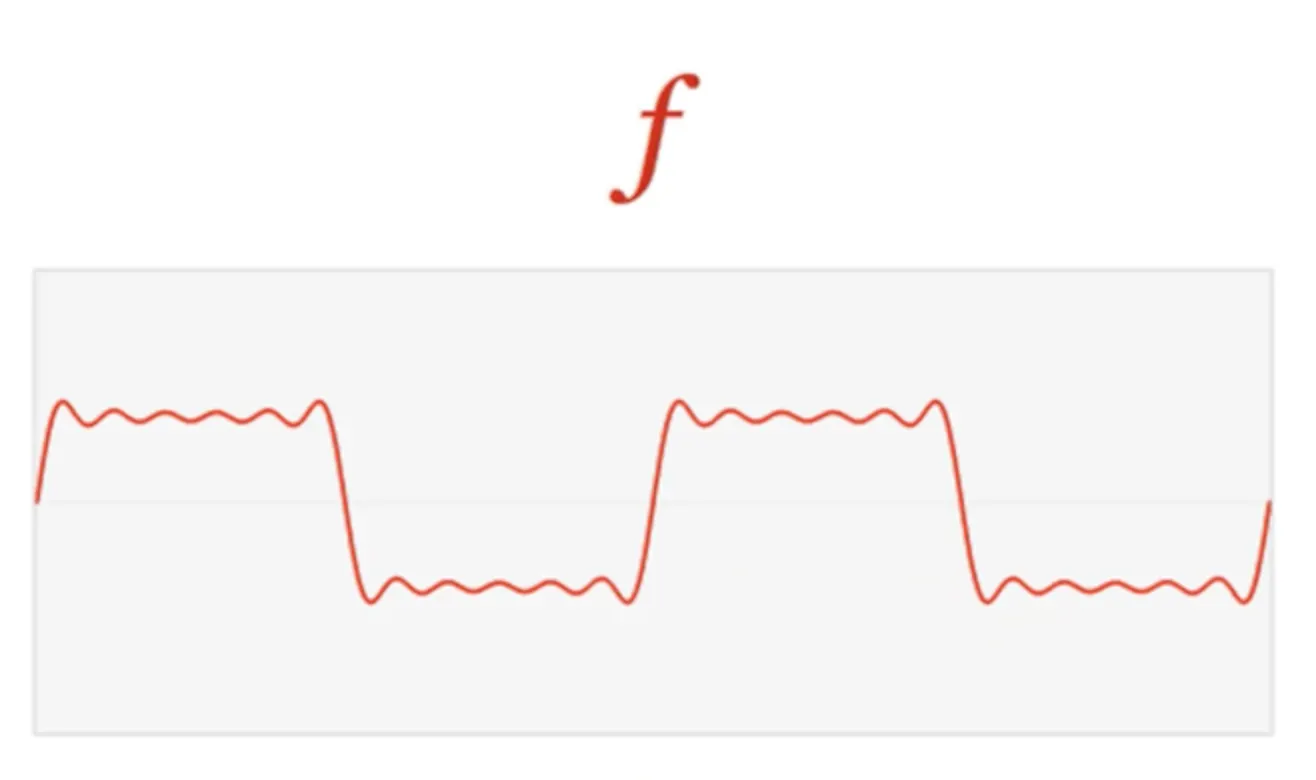
주기함수는 진폭과 주파수가 다른 사인파와 코사인파의 합으로 표현할 수 있는데, 무한개의 사인파/코사인파 또는 유한개의 사인파/코사인파로 표현할 수 있다. 무한 개의 사인파/코사인파로 표현해야 하는 함수를 유한 개만 사용하는데 더 많은 함수를 사용할수록 더욱 정밀해진다.
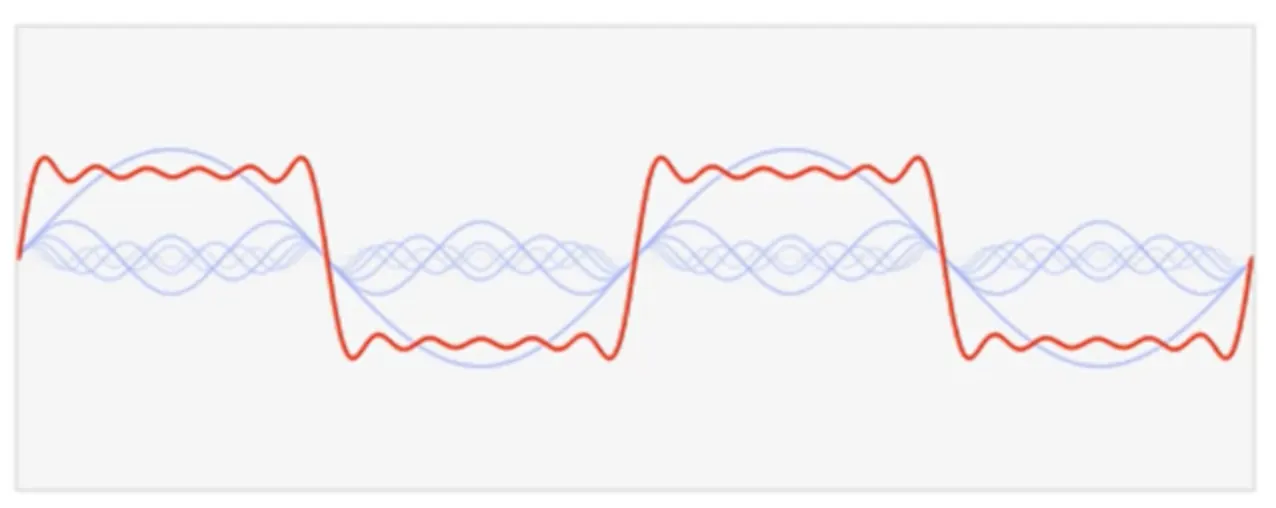
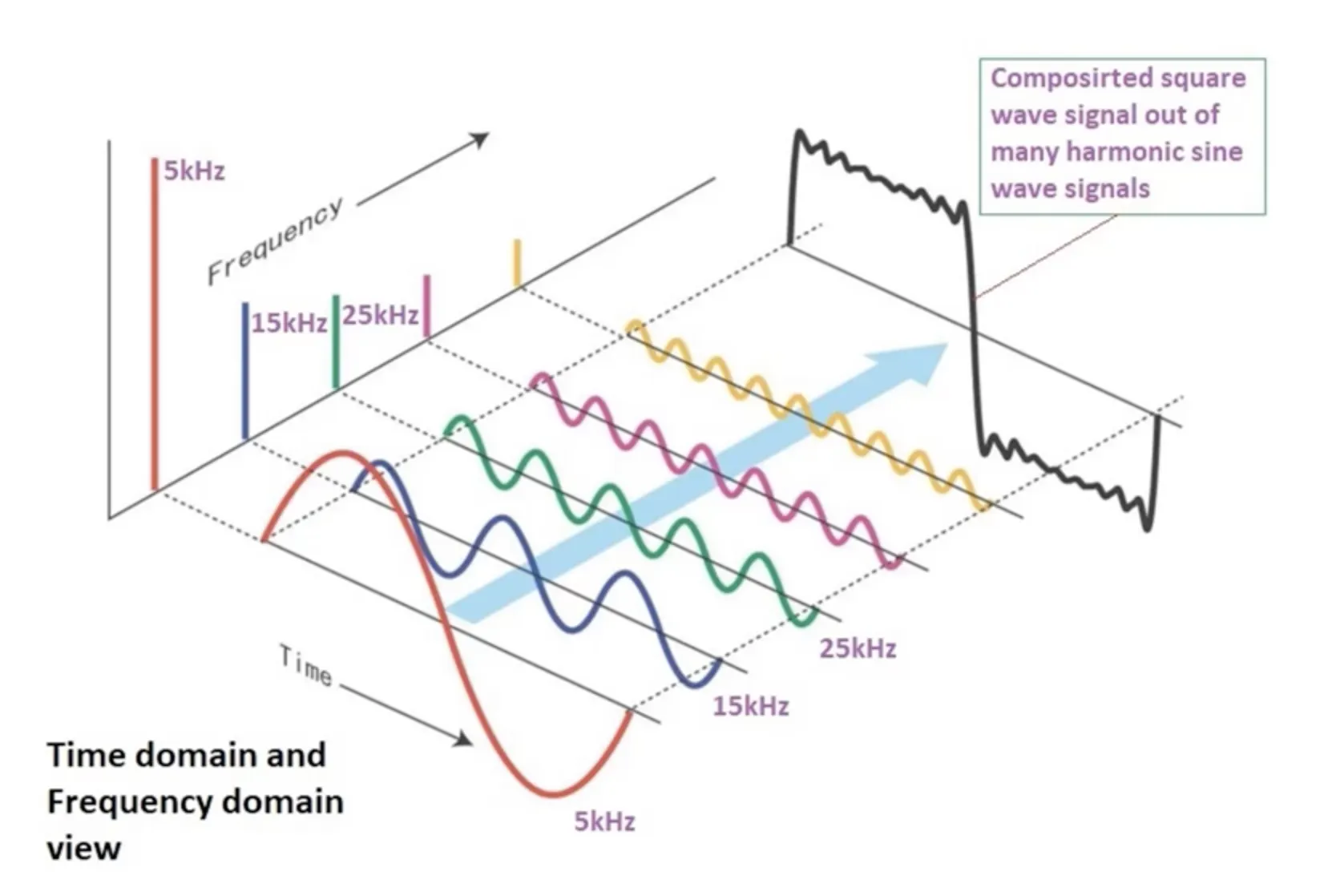
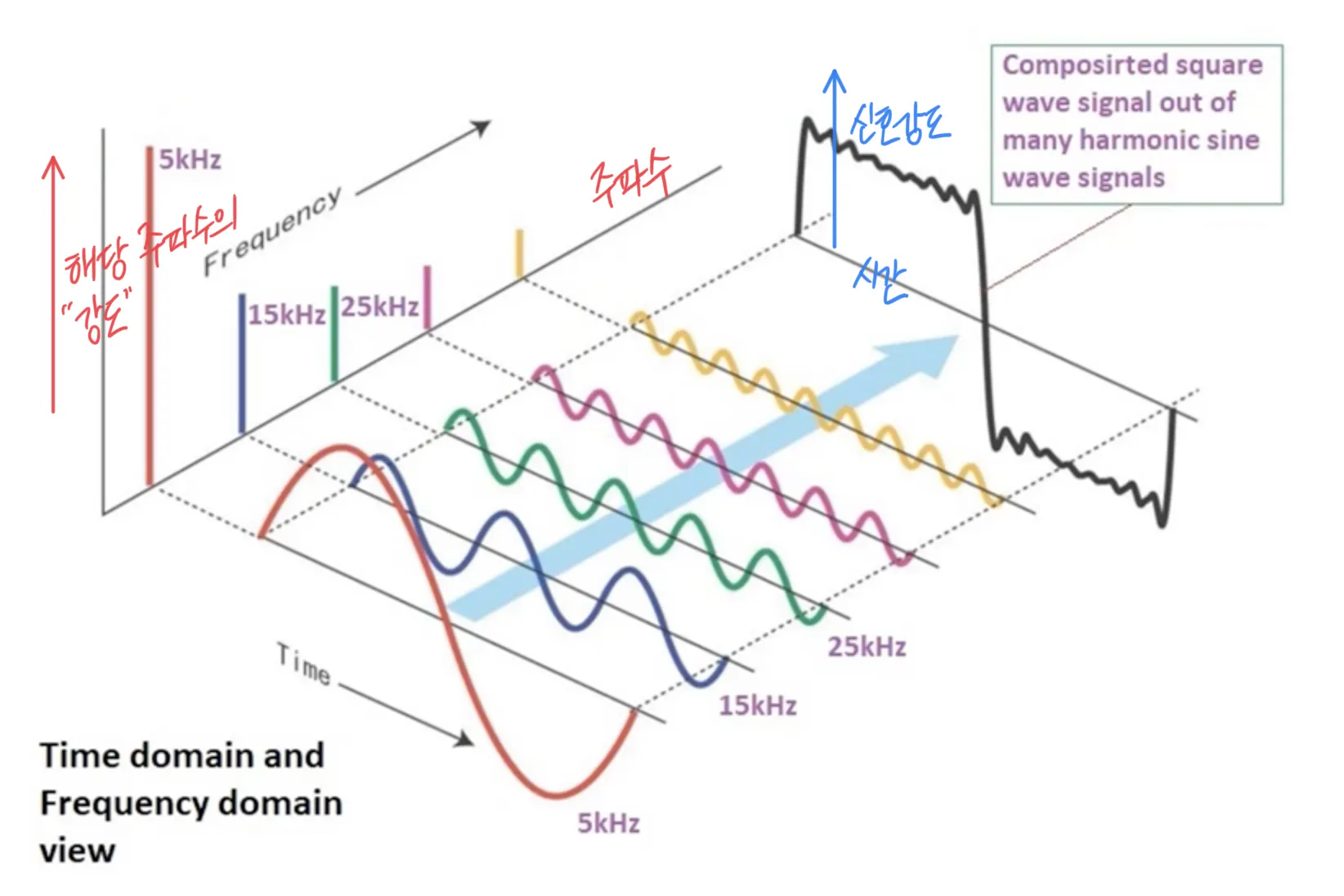
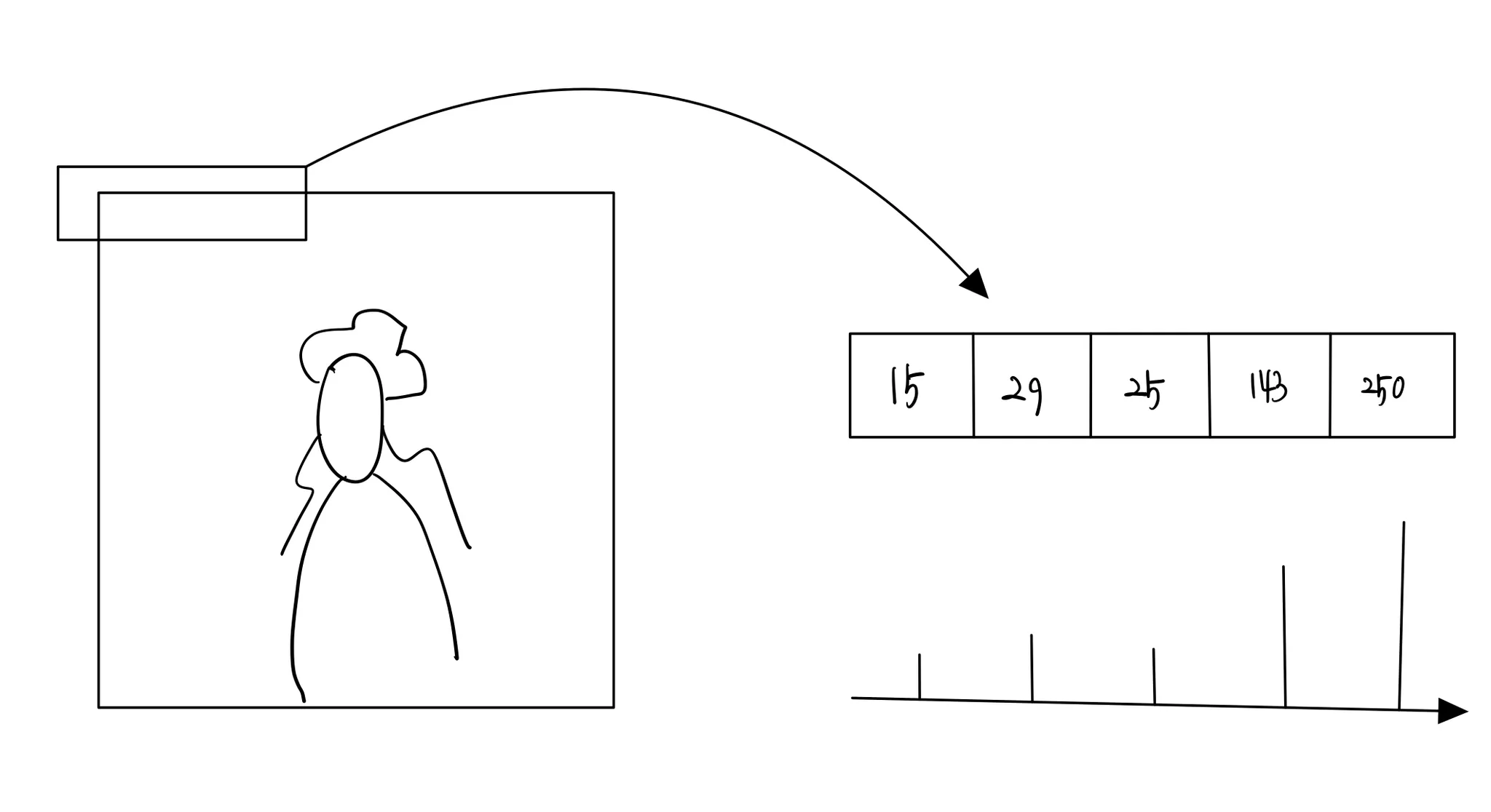
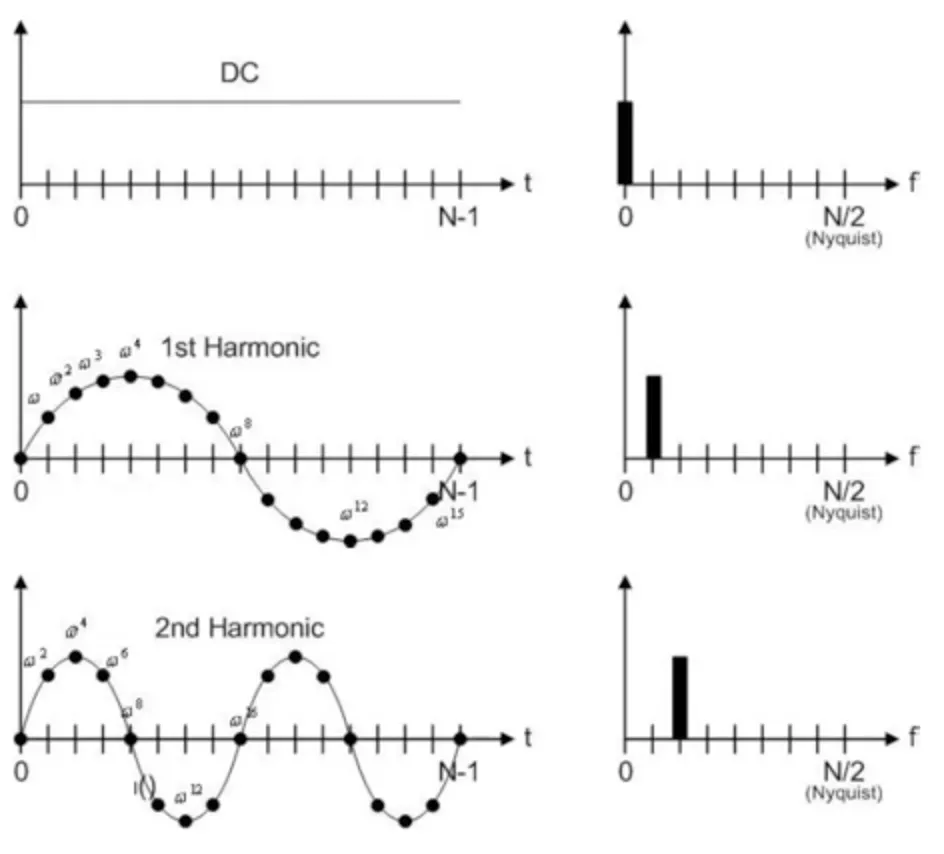
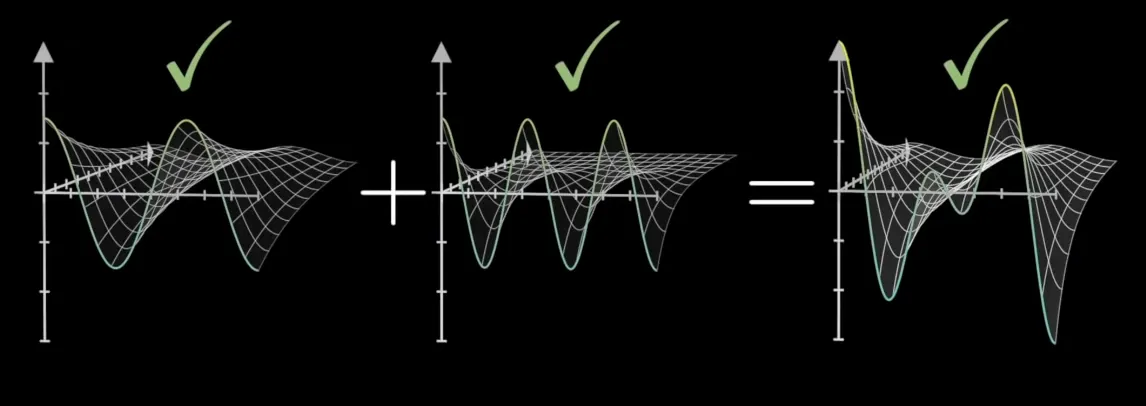
신호를 분리한다는 컨셉을 직관적으로 그린 그림이다.
좌 : 시간 도메인, 우 : 주파수 도메인
공간축으로 해석하느냐 (우리가 6장까지 배웠던 것), 시간 축으로 해석하느냐 (아래 그림) 주파수 축으로 해석하느냐 (아래 그림) 에 따라서 관점이 달라진다.
이제 위 내용들을 통해 어느정도 "주기 표현" 이라는 것에 대해서 감이 잡혔다면, 관련된 그래픽을 통해 극단적인 경우를 한번 구경해 보자.
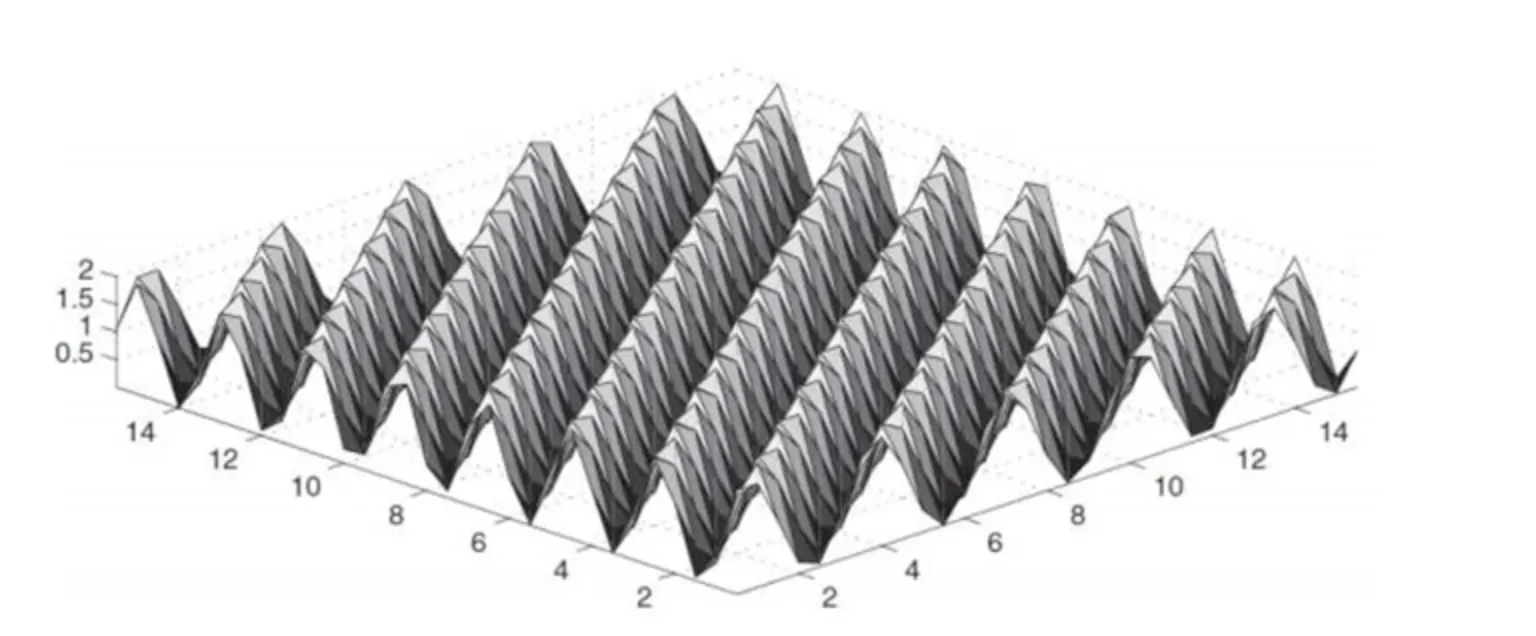
주파수 표현을 통해 톱니바퀴 비스무리한 것 그리기
위 그림을 굳이굳이 식으로 표현하자면 이렇게 표현할 수 있겠다.
물론 위 그림에서는 모든 주기 벡터 v 가 전부 원형이므로, a = b 라고 할 수 있다. 주기함수 를 시간 () 이 일정하게 흐른다는 전제 하에 벡터의 종점을 시각화한 결과이다.
비슷한 컨셉으로, 푸리에 급수로 푸리에 그리기
벡터들의 합이 이루는 종점이 시간 t 에 따라 변화하면서 그려내는 복잡한 형상들도 결국 돌고 돌아 제자리로 돌아온다면 주기함수라고 할 수 있다. 즉, 세상에서 주기가 있는 모든 것들은 푸리에 급수로 표현가능하다고 할 수 있다.
참고 : 아래 영상을 보면 상당히 많은 의문이 해소가 된다.
•
주기함수라는 것에 도대체 무슨 의미가 있나.
•
도대체 복소수는 왜 가져온 것인가. (스포하자면, 정말로 그냥 "대수적 표현의 편의" 를 위해서이다. 실수를 x 축, 복소수를 y 축으로 두는 complex plain 에서 정말 깔끔하게 원이 그려지는 모습을 통해 확인할 수 있다.)
•
도대체 불연속함수 (e.g. step function) 을 푸리에급수로 어떻게 표현을 하겠다는 것인가.
•
푸리에급수는 결국 "근사시키는 것" 을 의미하는데, 그것이 어떻게 과연 믿을 수 있는 연산인 것인가.
보고 보고 또 보자.
배경 지식 : 푸리에 변환 (Fourier transform) / 이산 푸리에 변환 (Discrete Fourier transform)
푸리에 변환 (fourier transform)
영상처리를 위해 식을 알아야 할 필요는 없다는 사실을 잊지 말자.
푸리에 변환은 푸리에 급수의 확장으로, 임의의 비주기함수 (주기가 무한임) 를 삼각함수들의 조합으로 표현하는 것을 의미한다.
주기함수에 한정지어서 표현할 수 있었던 푸리에급수의 한계를 벗어던진 일반형이라고 할 수 있다.
참고 : 오일러 공식
위 푸리에 변환식을 오일러 공식을 활용해 다시 표현하면 아래와 같다.
영상처리를 위해 식을 알아야 할 필요는 없다는 사실을 잊지 말자. 이런 형태로 어떻게 변환되는지는 공업수학 / 신호처리에서 배우자.
의미적 설명
: 원본 신호
: 로 표현된 주기신호. 의 값에 따라 최소주기가 다른 신호일 것이다.
오일러 공식을 통해, 복소수 e 와 cos, sin 의 관계를 서술할 수 있다.
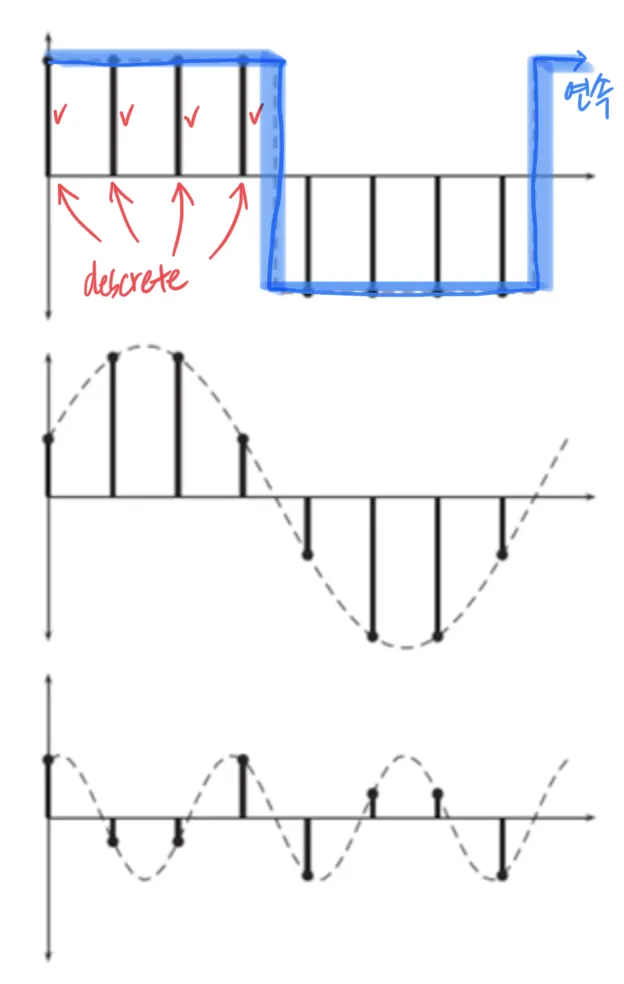
이산 푸리에 변환 (discrete fourier transform), DFT
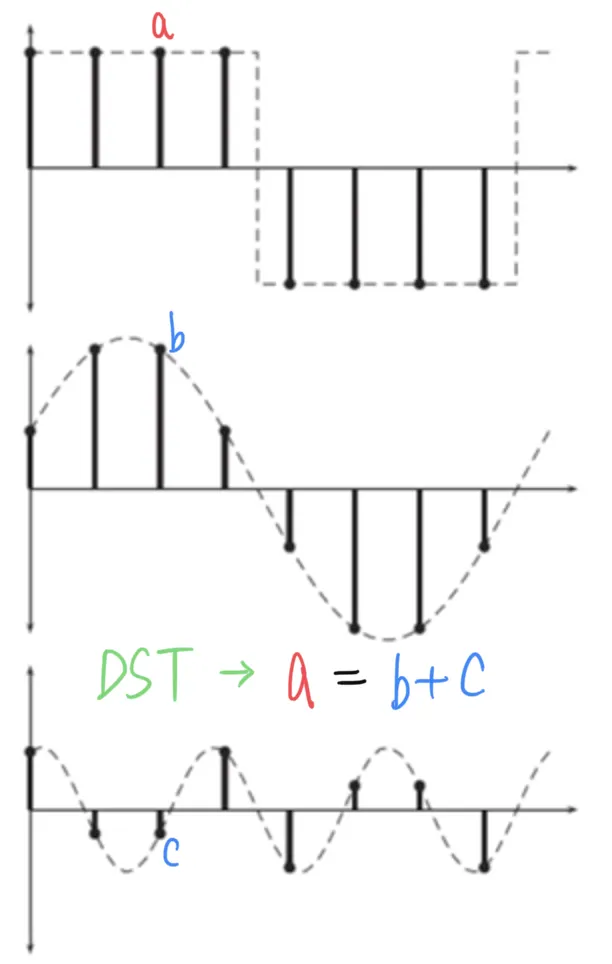
위 그림은 연속함수를 분해하는 것과 불연속함수를 분해하는 것의 차이를 직관적으로 보여준다.
아래 식은 DFT 의 수식이다.
의미적 설명
: 원본 신호
: 로 표현된 주기신호. 의 값에 따라 최소주기가 다른 신호일 것이다.
푸리에 변환은 연속함수에 대해서만 정의된다. 영상은 불연속이기 때문에, DFT 만을 다루게 된다.
FIXME : DST → DFT
쉽게 말해서 이산 푸리에 변환 (DFT) 은, 이산적으로 존재하는 신호들끼리 더해서 이산적으로 존재하는 신호를 만들어 낼 수 있음을 의미한다.
remind : 왜냐하면, 이산적인 신호도 아날로그 (연속 주기신호, 연속 비주기신호) 신호와 같이 해석할 수 있고 → 모든 비주기신호도 다양한 주기를 가진 삼각함수들의 합으로 표현할 수 있고 → 주기로 분해된 삼각함수들은 요소들을 강하게 만들거나 약하게 만드는 것이 자유롭기 때문이다.
내가 가질 수 있는 직관은 이 정도였다.
1. 10개짜리 이산 신호를 온전히 복원하기 위한 주파수의 개수는, 10개이다. 만약 10개짜리 이산 신호를 10개보다 적은 주파수를 통해 표현하려고 한다면, 신호의 일부분이 손상되거나 삭제될 수도 있다. 즉, N 개의 신호를 정확히 복원해내기 위해서는 최대 N 개의 주파수가 필요하다. (뭔가 당연한 이야기.)
이것은 아래와 같은 정리들을 내포한다.
- N 개보다 더 많은 주파수는 필요 없다.
- N 개보다 적은 개수의 주파수만을 사용해서 손실 없이 신호를 표현할 수 있다.
- N 개보다 적은 개수의 주파수를 사용했을 때, 손실이 발생할 수도 있다.
2. exponential 의 지수에서 볼 수 있는 u 값이 클수록, x 의 계수가 높아지는 것이기 때문에 주기가 짧은 고주파 성분을 나타낸다.
1차원 DFT 의 정의
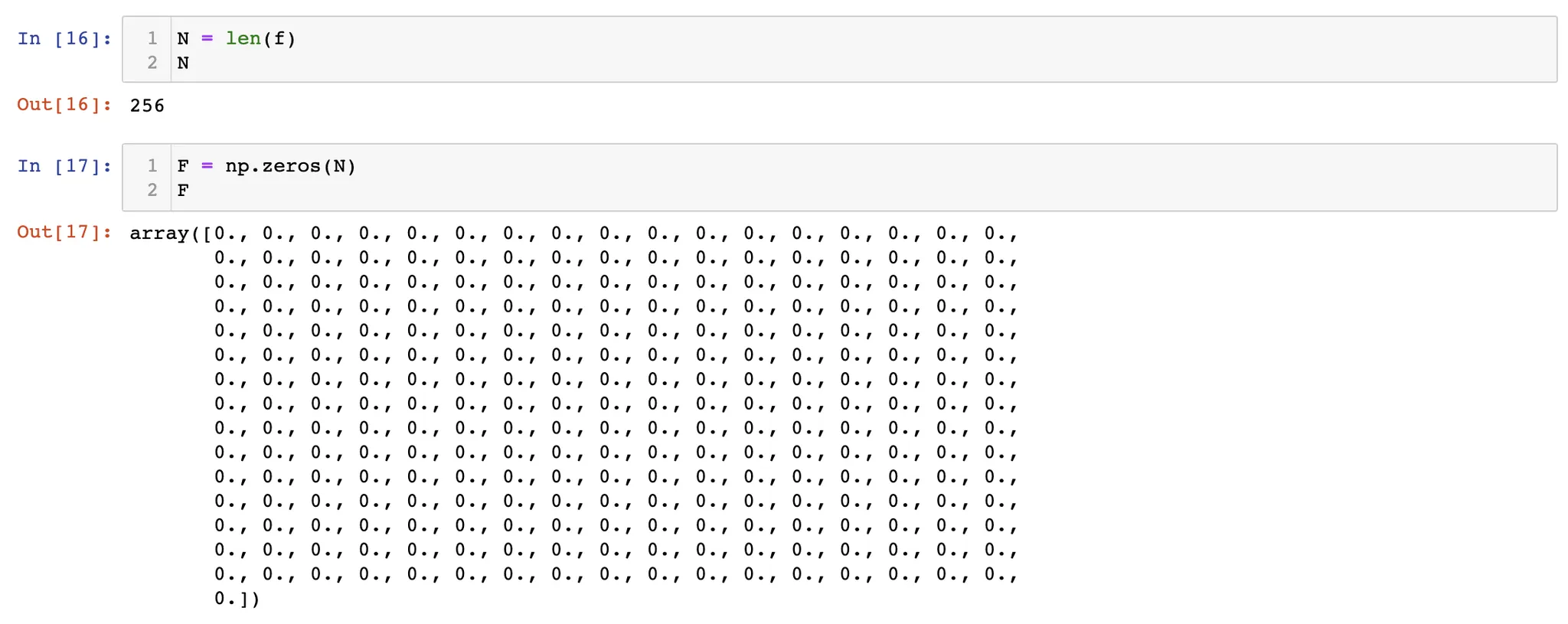
앞으로 우리가 사용할 notation 이자, 벡터 또는 행렬 f, F 이다. f 는 원본 신호, F 는 DFT 된 신호를 나타낸다.
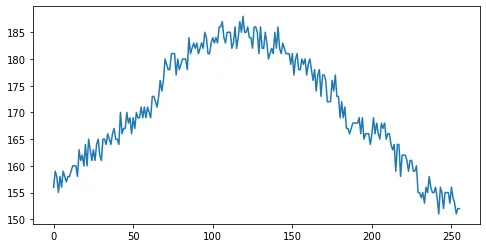
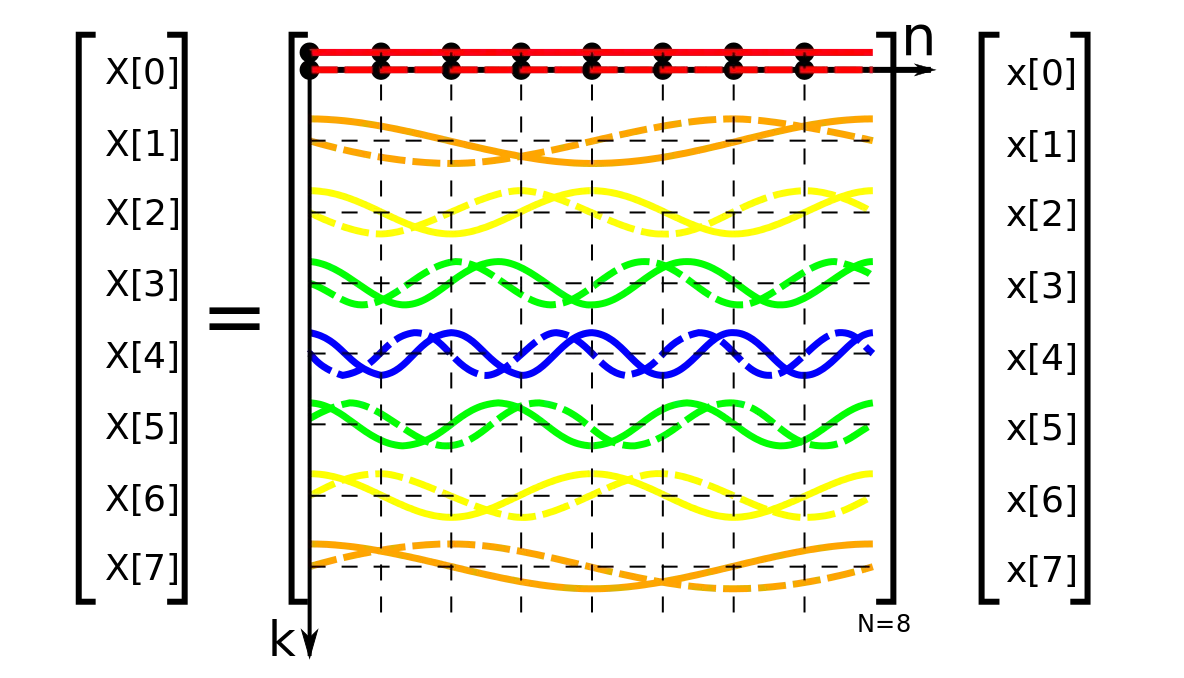
아래의 왼쪽 이미지에서 0행만 뽑아서 관찰한다면 아래의 오른쪽과 같은 결과를 얻을 수 있다.
f = im[0,:]
plt.figure(121, figsize = [8,4])
plt.plot(f)
plt.show()
Python
복사
잊지 말자! 여기서 뽑아낸 0행 을 주파수 신호 로 분해하는 것이 목표이다. 이 식에서 는 이미지의 가로 길이이다.
이를 하기 위해서는 아래 식을 다시 떠올려야 한다.
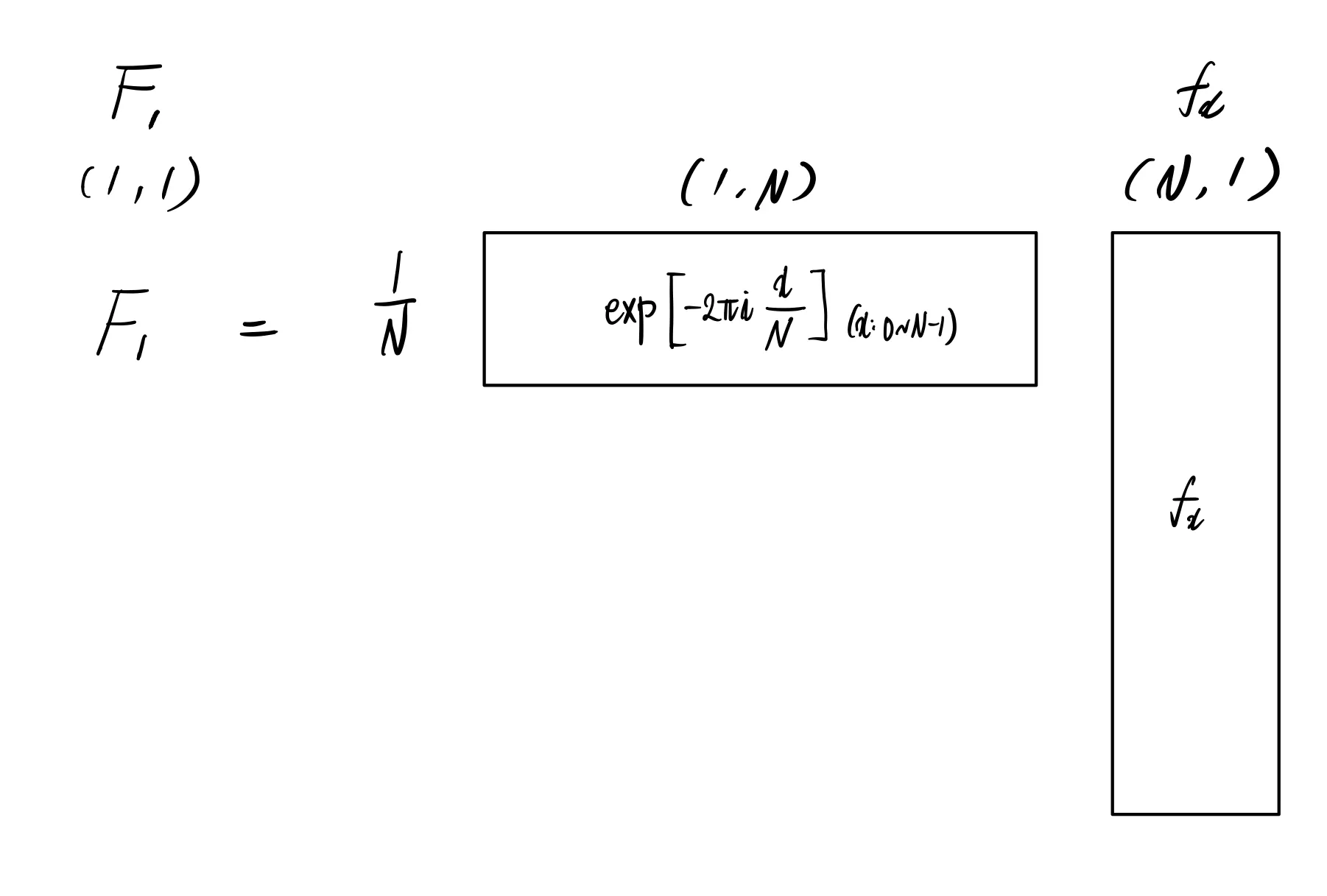
의 에 대한 관계식을 보자. 그리고, 우선 인 경우만 생각해 보자.
잘 생각해 보면, N 은 상수이므로, 아래와 같이 matrix 로 표현 가능하다. 연산결과는 scalar 이고, 각 벡터의 shape 은 (1,N) (N,1) 이다.
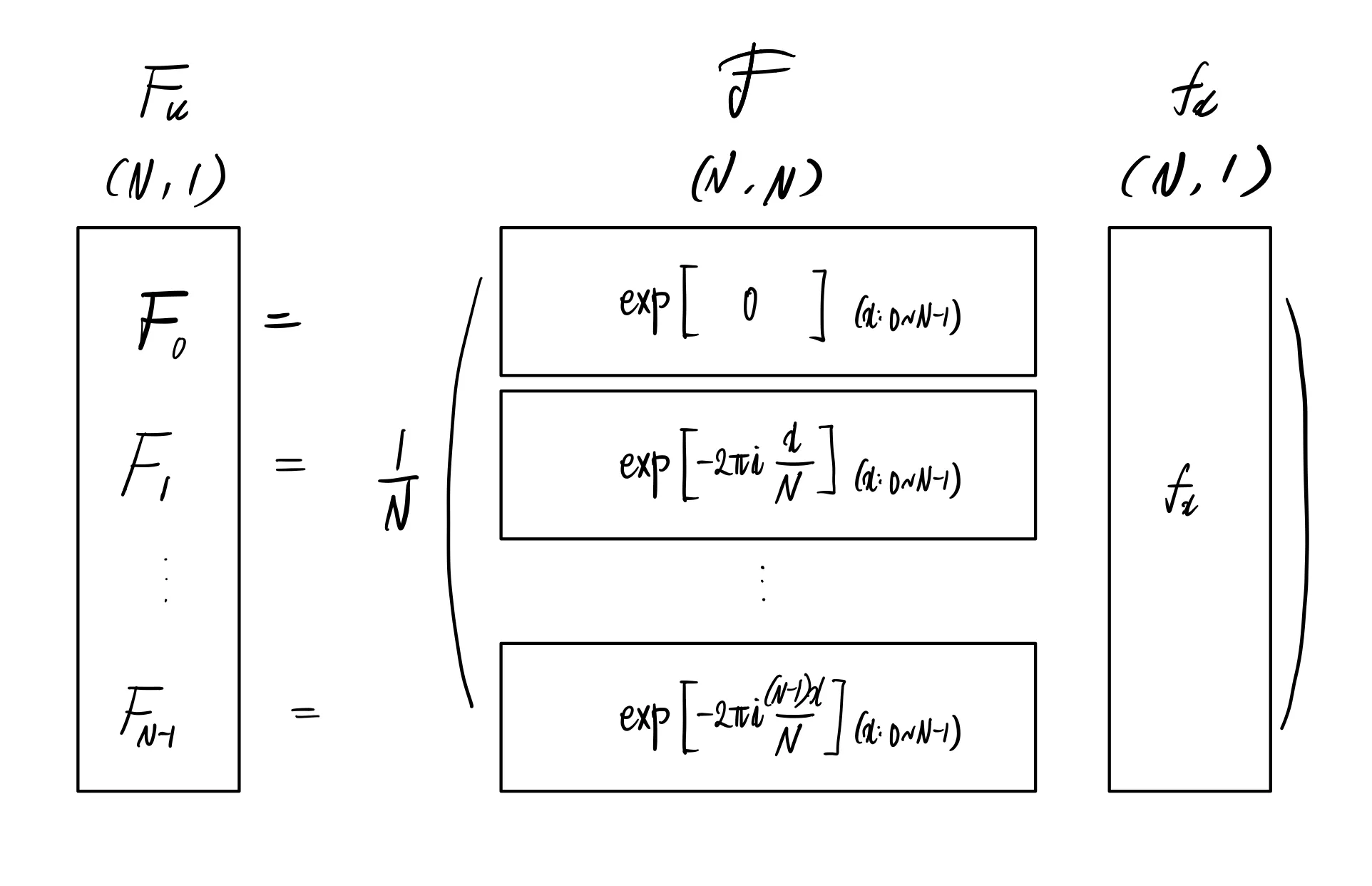
그렇다면 이제 이를 까지 모두 얻기 위해서 matrix 는 다음과 같아야 한다.
이때 나타나는 (N,N) size 의 행렬을 DFT 행렬이라고 한다. (DFT matrix is a transformation matrix, which can be applied to a signal through matrix multiplication.)
위키피디아
이 이미지를 보면 이런 생각이 들기도 한다.
엥 뭐야 그냥 correlation 을 구하는 느낌인데? 분해하고자 하는 어떤 신호가 있고, 원본 신호와의 correlation 을 구하면 해당 영상에 어떤 성분이 얼마나 관여하고 있는지 파악할 수 있겠지.
또한, 신호처리의 관점에서 convolution neural network 을 설명할 수 있을 것 같은데,
배경 지식 정리 : 푸리에급수 → 푸리에변환 → 오일러식 → 이산푸리에변환 (DFT)
길고 긴 내용들이 장황하게 왔지만, 한번 모아서 정리해 보도록 하자.
1차원 푸리에급수에서 원본신호 f 와 주파수신호 F 사이의 관계식
1차원 푸리에변환에서 원본신호 f 와 주파수신호 F 사이의 관계식
1차원 푸리에변환에서 원본신호 f 와 주파수신호 F 사이의 관계식 (오일러 공식 적용 후)
오일러공식을 적용한 1차원 원본신호 f 와 주파수신호 F 사이의 푸리에변환 관계식에서, 이산적인 경우로 생각을 확장한 이산푸리에변환식 (DFT)
1차원 원형 회선 (1D Circular Convolution) 과 회선 정리 (Convolution Theorem)
원형 회선은 1차원 필터링 (1D filtering) 과 함께 배웠던, 1차원 회선 (1D convolution) 과 비슷한 개념이지만, 단지 y 의 index 를 벗어났을 경우 어떻게 생각하느냐의 차이만 존재한다.
spatial filtering 과 spatial convolution 에 대해서
Circular Convolution (원형 회선) 표기에서 음수 index 는 y 가 "periodic" 하다고 생각하고 얻는다.
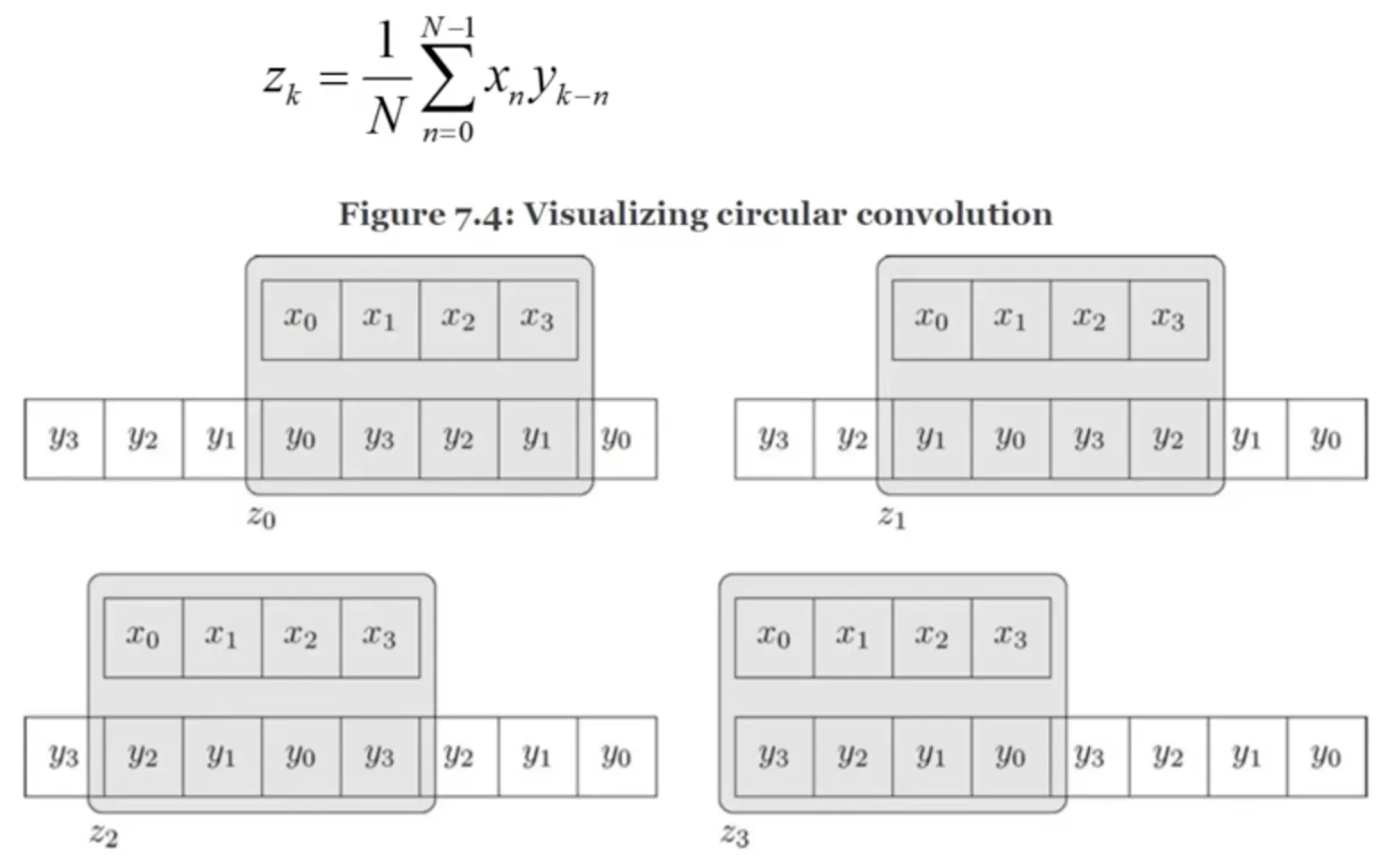
아래는 벡터 x, y 의 길이가 N 으로 동일할 때 성립하는 수식과 그림이다.
사실 나는 이러한 다변수 연산이 익숙하지 않다. 조금이라도 더 와닿기 위해, 귀납적으로 한번 계산을 해본다.
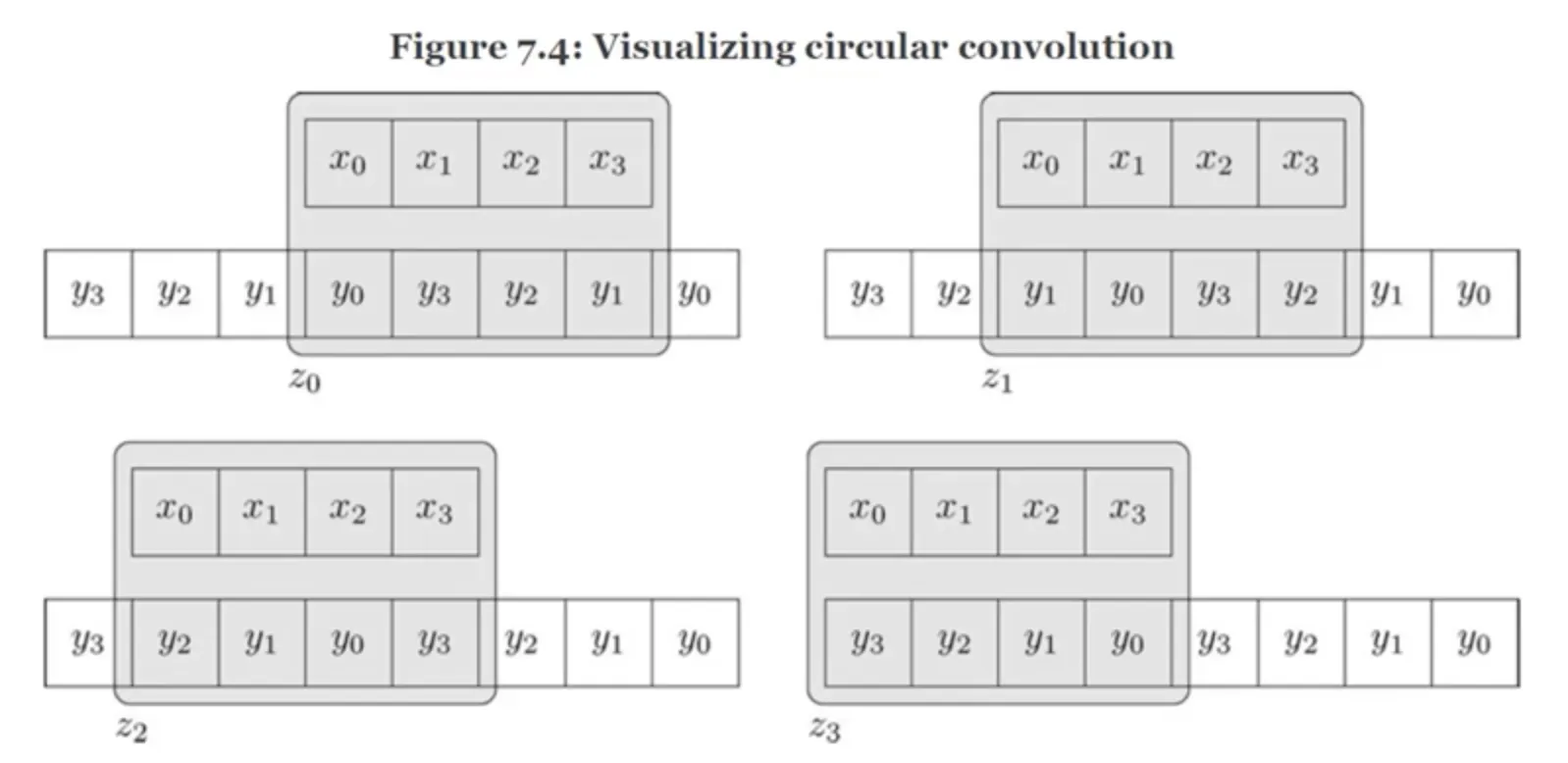
위 그림과 같이, N=4 인 경우, Circular Convolution
•
벡터의 이동 횟수 : k
•
1회 이동 당 연산 : 4 (정확히는 곱셈연산 4회, 덧셈연산 4회)
•
벡터 z 의 값 : 주기 4 (N) 마다 반복되는 형태로 다음과 같은 형태이다.
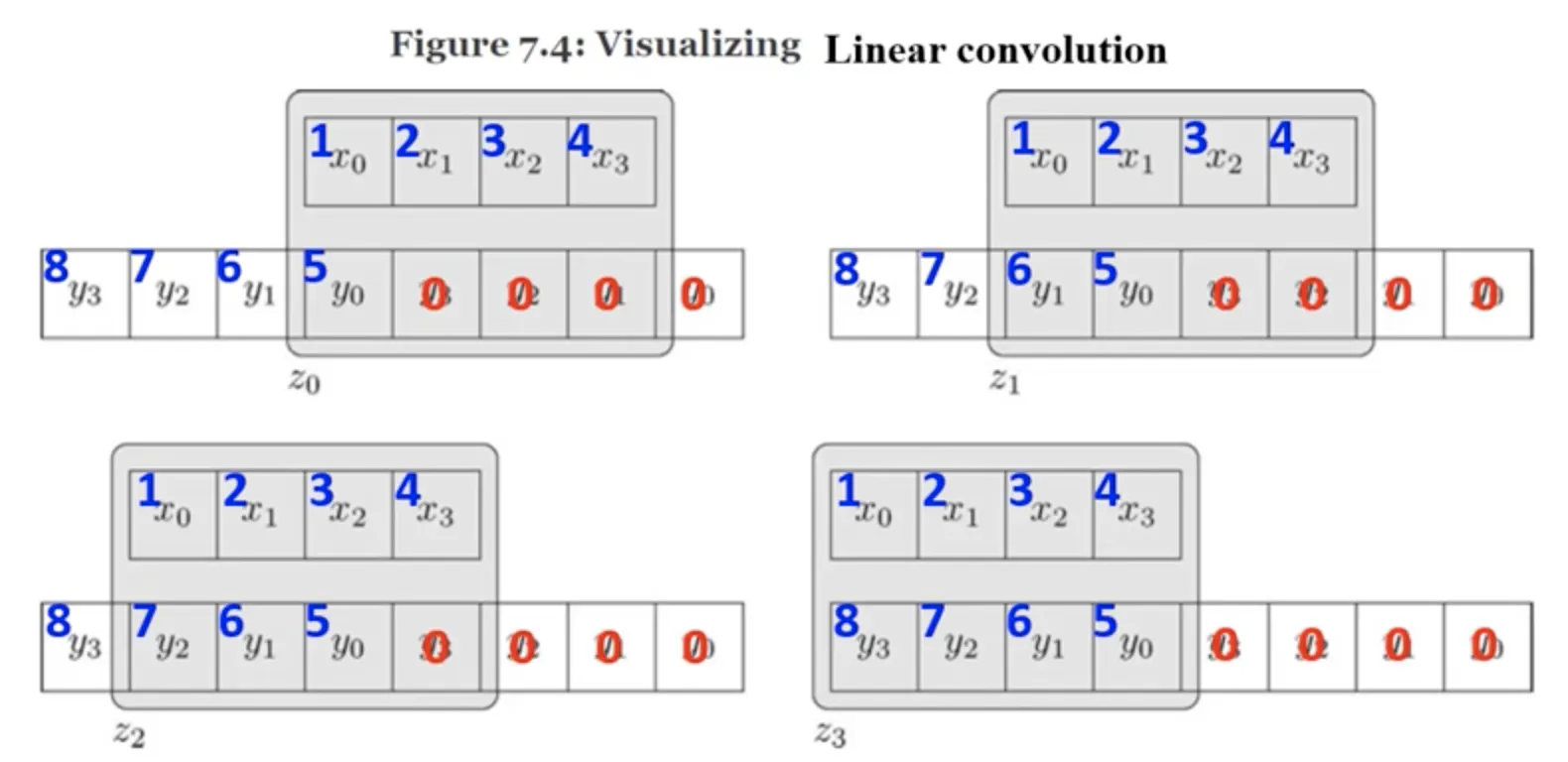
Circular Convolution 과 Linear Convolution 을 비교한 그림이다.
위 그림과 같이, N=4 인 경우 Linear Convolution
•
벡터의 이동 횟수 : k
•
1회 이동 당 연산 : 4 (정확히는 곱셈연산 4회, 덧셈연산 4회)
•
벡터 z 의 값 : 다음과 같은 형태이다.
(우선 1차원 신호들에 대해서만 생각해 보자) 선형회선 연산을 통해 원형회선 결과물을 얻으려면, 선현회선의 대상이 되는 벡터를 두 개 이어붇히고 연산에 0이 포함되지 않은 채 반복되는 부분을 뽑아내면 되지 않을까?
사실 강의를 듣다가 지난 시간에 등장했던 회선과 조금 다른 모습의 회선이 이제서야 등장해서 조금 이해하기 어려웠는데, 강의의 맥락상 뜬금없이 원형 회선이 등장한 이유는, 회선 정리를 설명하기 위함이 아니었을까 생각한다.
회선 정리 (Convolution Theorem) 두 벡터 x, y 가 동일한 길이의 벡터라고 할 때,
x 와 y 의 DFT (Discrete Fourier Transform) 의 element-wise product (correlation 연산) 과 x 와 y 의 convolution 연산의 결과물은 동치이다.
수식으로 표현하면 다음과 같다.
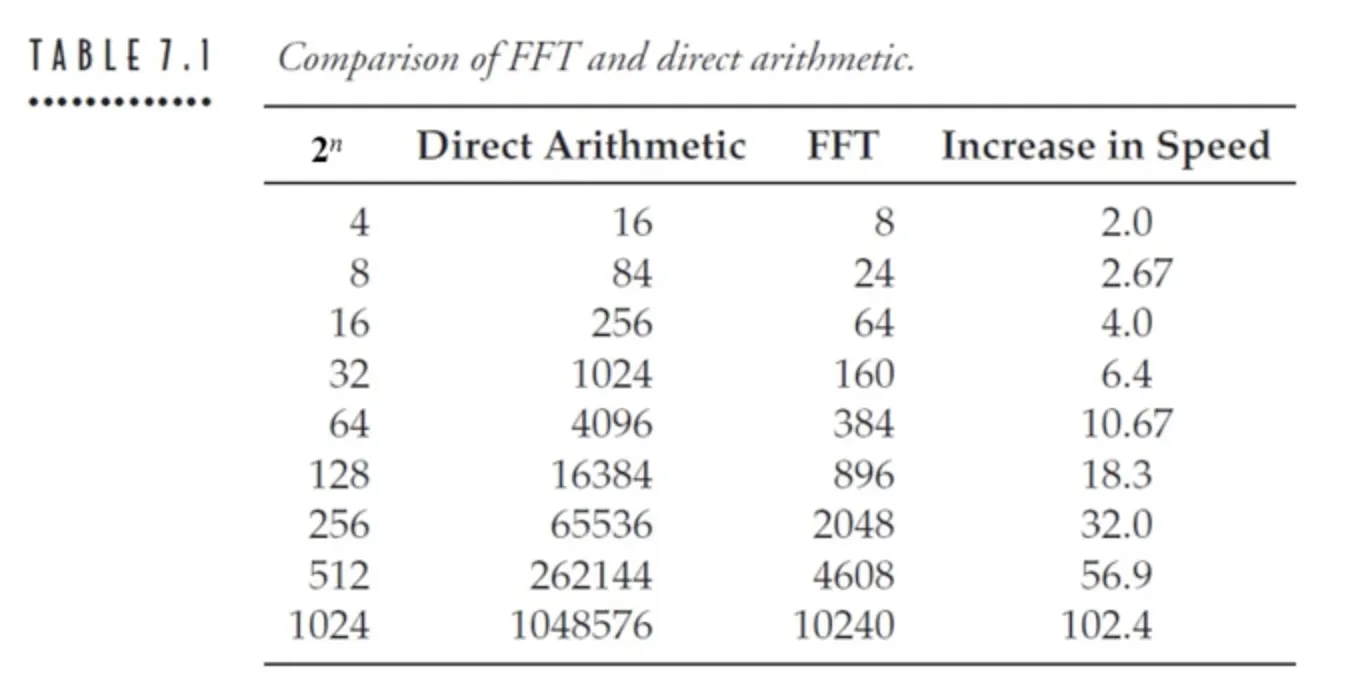
참고 : 고속 푸리에 변환
DFT 를 빠르게 계산하는 알고리즘이 있다.
FFT (Fast Fourier Transform) 은 DFT 를 빠르게 계산하는 알고리즘이다.
2차원 이산 푸리에 변환 (2D DFT)
1차원 DFT 의 경우, input : vector (length 가 N인) , output : vector (length 가 N인) 이었다.
2차원 DFT 의 경우, input : matrix (size 가 N,N 인) , output : matrix (size 가 N,N 인) 이다.
앞에서 배웠듯, 1차원 신호는 sin 과 cos 함수의 합으로 표현할 수 있었다.
2차원 신호인 영상 f(x,y) 는 주름 (corrugation) 함수의 합으로 표현될 수 있다.
하나의 주름함수는 아래 식과 같이 표현할 수 있다.
주름함수의 합으로 분해한다는 개념이 잘 와닿지 않는 경우, 아래 3blue 1brown 의 영상에서 실컷 시각화를 볼 수 있으니 참고하도록 하자.
다시 돌아와서, 영상과 주름함수 사이의 관계는 다음과 같다.
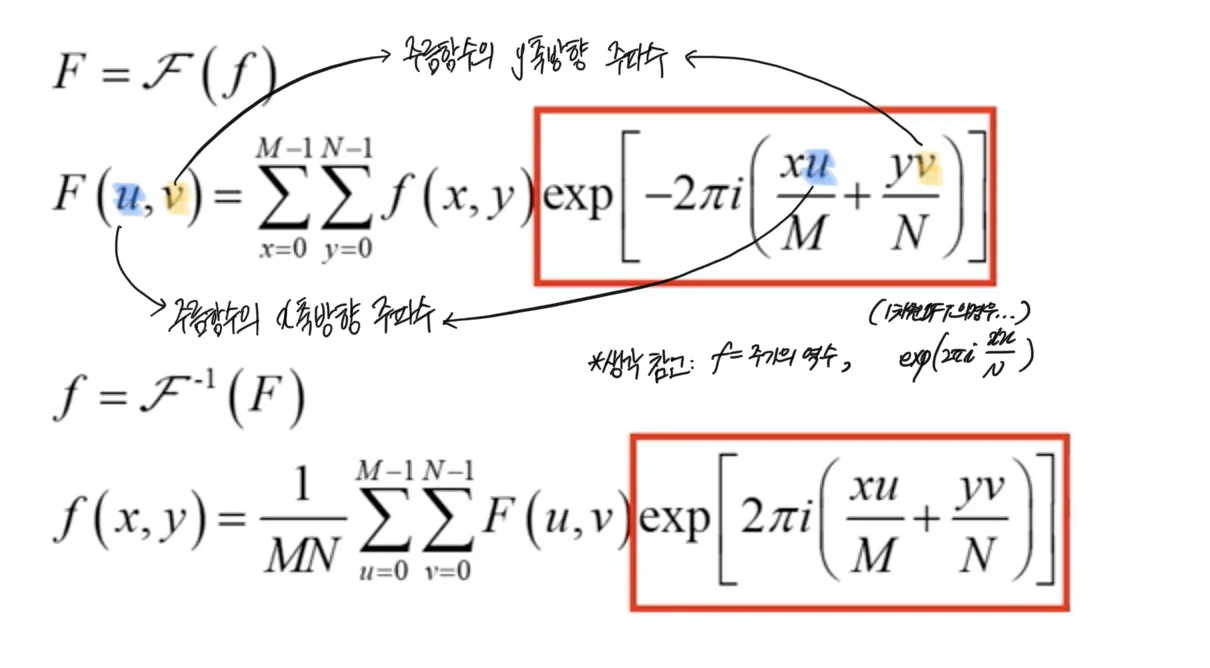
u 와 v 가 무슨 의미를 가지는지 생각을 해 보자.
•
u : 주름함수의 x 축 방향 주파수와 관련된 값
(정확히 주파수는 아니지만, 그런 의미를 담고 있다는 뜻.)
•
v : 주름함수의 y 축 방향 주파수와 관련된 값
(정확히 주파수는 아니지만, 그런 의미를 담고 있다는 뜻.)
두 변수가 어떤 의미를 가지는지 이해를 했다면, 아래와 같은 그림을 우선 한번 보자. 이미지를 통해 주파수 도메인의 신호 F 를 시각화한다면 어느 모습으로 나타나는지 간단히 알아보도록 하자.
아래 그림에서 가운데 이미지는 이미지 a 를 푸리에 변환한 것이고, 우측 이미지는 그냥 푸리에 변환된 이미지를 잘 보이게 스케일링한 것일 뿐이다.
정확히 말하면, 가장 우측의 이미지는 단지 스케일링했을 뿐 아니라 DFT 의 Shifting 이라는 성질을 이용하여 중앙에 저주파성분이 오도록 옮긴 것이다. 하지만, 우선 지금은 그런 것 없이 그냥 중앙의 이미지를 rescale 한 값이고, DFT 된 주파수영역의 이미지를 visualize 하는 것이라고 생각해 보자.
이 이미지를 잘 보면, 가운데 하나의 값만 매우 높은 것을 알 수 있다. 이 값은 잠시 후 배울 DC 라는 값이다. 하지만 지금은 그냥 DFT 의 결과물이라고 생각을 하자.
이 그림에서, 이 각각의 픽셀들이 가지는 의미가 무엇일지 생각을 해 보자. 각 픽셀들이 가지는 intensity 는 (물론 Log 함수로 rescale 되었지만) 주름함수에서 각 u, v 와 관련된 주파수를 가지는 요소들이 얼마나 들어있는가를 나타낸 것이다. 중앙 부분이 가장 밝은 것을 보면, 대충 u=w/2, v=h/2 과 관련된 주파수*를 가지는 요소들이 가장 많이 들어있지 않을까? 하는 상상이 가능하다.
*해당 주파수가 아니고 '관련된' 주파수라고 하는 이유는, 아까도 말했지만 u 와 v가 주름함수를 구성하는 두 변수 x, y 의 주파수를 정확히 의미하지는 않기 때문이다. 하지만, u 와 v 는 x와 y 의 계수이므로, u 와 v 가 높을수록 더욱 고주파를 나타낼 것이라는 상관관계 정도는 알 수 있다.
참고 : 물론 실제로 이 이미지에서 중앙은 DC coefficient 이다.
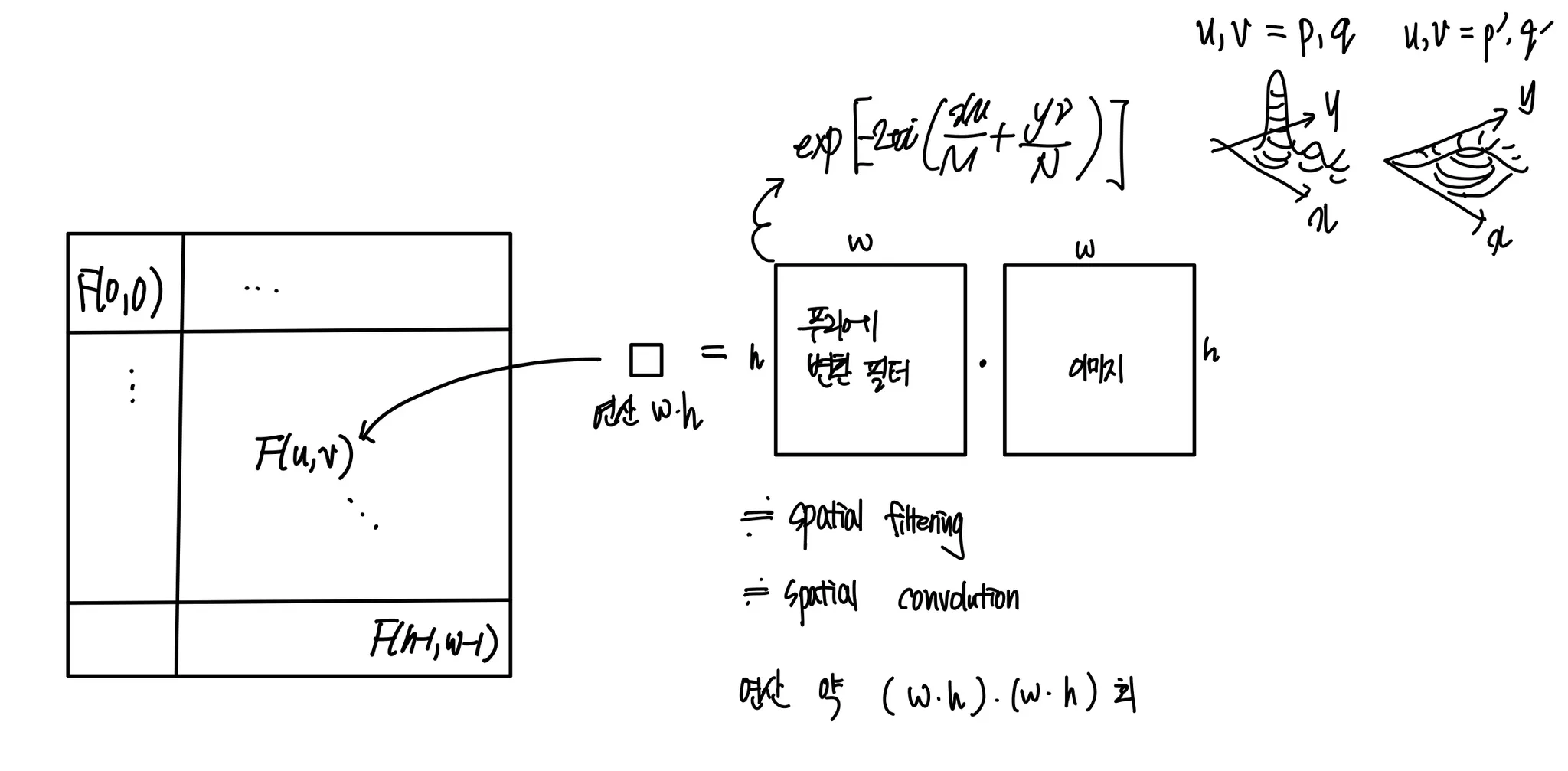
예를 들어, 을 계산하기 위해서는 만을 계산해 두면 되고, 이때 의 정체 는 input image 의 size 와 동일한 (N,M) matrix 이다.
input image 와 (N,M) matrix 와 곱해서 더하므로, 선형 공간 필터 (linear spatial filter) 라고 생각할 수도 있다. 그래서, NxM 개의 (N,M) 행렬을 fourier transformation matrix 라고 하기도 한다.
고차원 표현에 익숙한 사람은, 미리 만들어 둘 수 있는 matrix 의 shape 은 4차원:(N, M, N, M) 이라는 것을 짐작할 수 있을 것이다. 아무리 미리 만들어두어도 그렇지, (N, M, N, M) 은 너무 무겁지 않은가? 라고 생각하는 순간, 2차원 필터의 성질에 대해서 배운다.
2차원 DFT의 성질 : 분리성 (separability)
분리성 (separability) 는 2D DFT 가 2 x 1D DFT 로 분리가능한 성질이다.
원래 연산 횟수
간단하게 생각해서, F(u,v) 를 구하기 위해 sigma 가 두 번 있으므로, N*M 회 연산을 할 것이라는 사실을 알 수 있지만, 아래 그림에서 조금 더 좋은 직관을 얻어 보자.
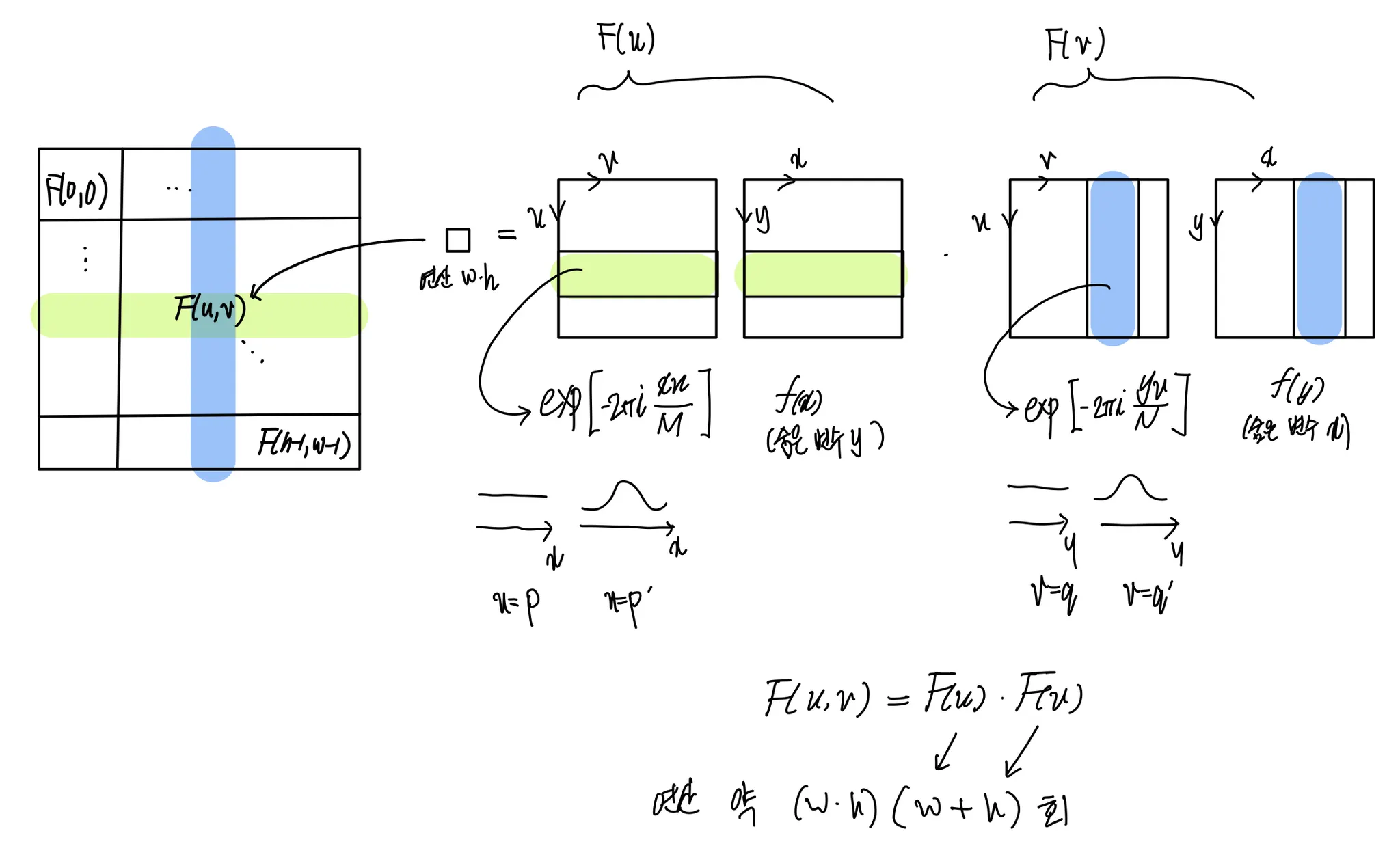
분리 필터 적용 시 연산 횟수
마찬가지로, F(u) 와 F(v) 를 구하기 위해 각각 sigma 가 한 번씩 있으므로, N+M 회 연산을 할 것이라는 사실을 알 수 있지만, 이것도 아래 그림을 통해 직관을 얻어 보자.
2차원 DFT 의 성질 : 선형성 (Linearity)
- 두 신호를 더한 것은 주파수 영역에서 두 신호를 더한것과 동일하다.
- 신호를 k 배 증폭시키는 것과 주파수 영역에서 k 배 증폭시키는 것이 동일하다.
2차원 DFT 의 성질 : 회선 정리 (Convolution theorem)
생각의 정리 를 잠깐 해 보자.
필터 연산은 공간 영역에서 회선 연산이다.*
회선 연산은 회선정리에 따라 주파수 영역에서는 원소별 곱셈 연산이다.
*글의 상단에서 언급했듯, 공간 필터는 필터 자체를 180도 돌려도 동일한 경우가 많다. 또한, 신호가 돌아간다고 해서 영상의 정보가 날아가고 하지도 않는다. 그래서, spatial filter 연산은 convolution 과 동일하다고 상정할 수 있다.
식을 한번 살펴보자.
좌변
•
M : 영상
•
S : 필터
•
: 영상과 필터의 Convolution 연산
우변
•
: Descrete Fourier Transform (DFT)
•
: 영상의 DFT 와 spatial filter DFT 의 elementwise product
여기서 주의해야 하는 것은, elementwise product 를 하기 위해서는 M 과 S 의 size 가 동일해야 한다는 것이다. 하지만 일반적인 상황에서, M 의 size 에 비해 S 의 size 가 작다. 는 과 동일한 사이즈로, 의 원래 크기를 제외한 모든 영역에 0 으로 마스킹이 되어있는 것이다.
해소되지 않는 의문
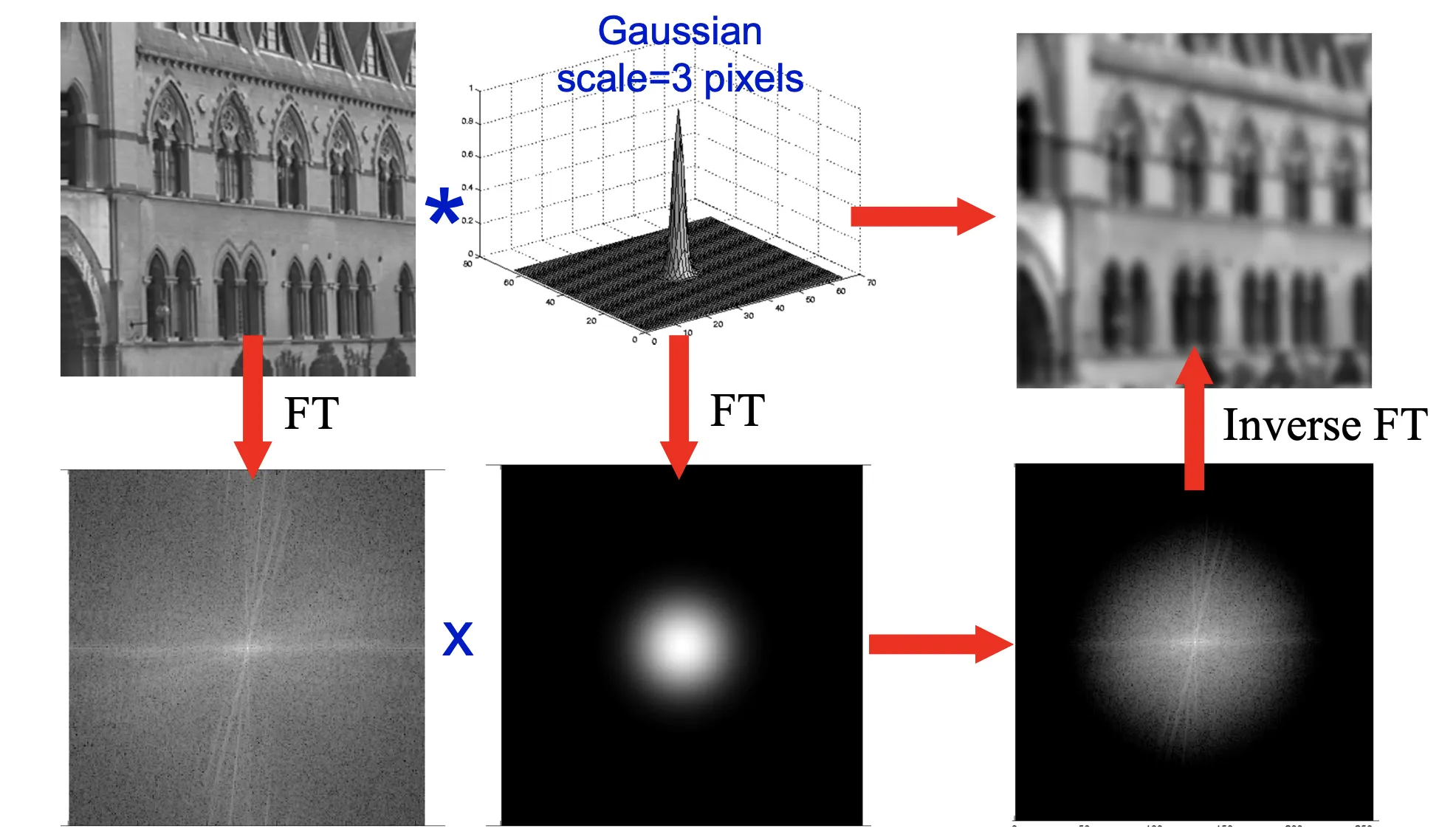
S 에다가 마음대로 0을 붙여서, S' 를 만들면, 원본 신호 S 의 의미가 훼손되는 것 아닌가? 라는 생각이 계속 드는데, 이 의문을 해소하기 위해서는 회선정리식을 유도할 수 있어야 할 것 같다. 그러므로 그냥 지금은 넘어가자.
위 의문의 해답이 될수도 있을만한 이미지이다. 정보가 없어지는 것이 맞다. 출처 https://www.robots.ox.ac.uk/~az/lectures/ia/lect3.pdf
회선정리를 통한 연산량의 절약
TODO
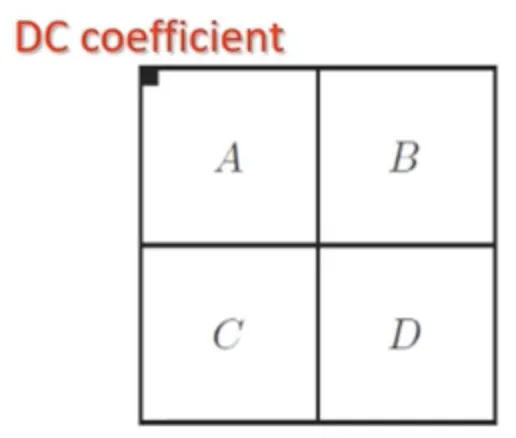
2차원 DFT 의 성질 : 직류 계수 (DC Coefficient)
DFT 의 F(0,0) 을 직류계수라고 한다.
영상의 intensity 를 가로, 세로방향으로 전부 더한 값을 의미한다.
2차원 DFT 의 성질 : 이동성 (Shifting)
이게 성질인가..?
이동성 (Shifting) 은 사람에게 보여주는 등의 디스플레이 목적으로 matrix 의 중심에 직류계수가 위치하도록 이동시킬 수 있다는 것을 의미한다.
Fourier Transform 된 결과의 크기를 디스플레이한 것을 Fourier Transform 의 spectrum 이라고 한다.
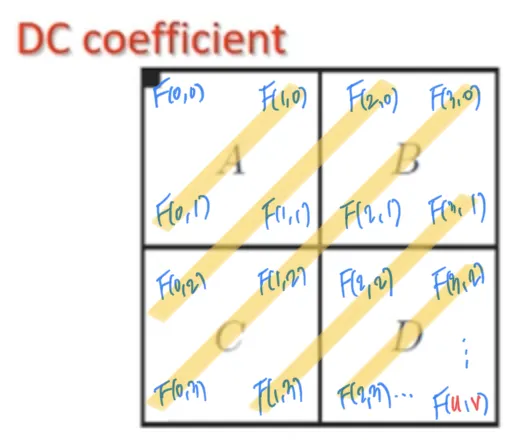
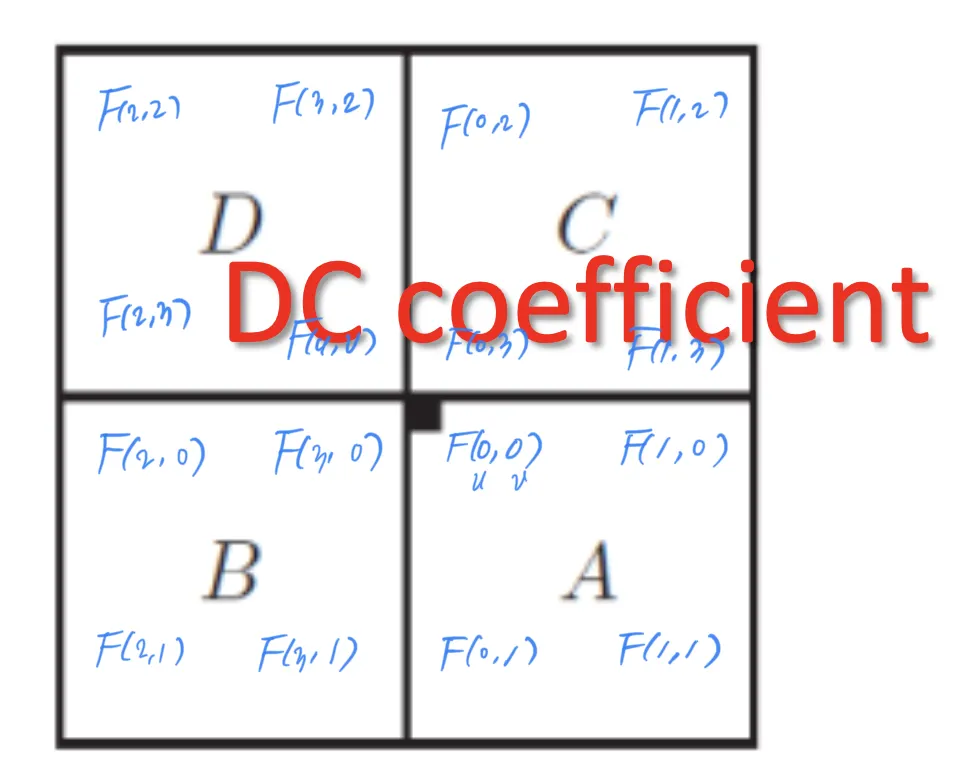
DFT 된 주파수 도메인의 결과가 이렇게 생겼다고 생각해 보자.
지난번에 언급하기를, 의 u, v 는 주파수와 밀접한 연관이 있다고 했다. 명확한 관계식은 알 필요가 없지만, 푸리에 급수 → 푸리에 변환 → 이산 푸리에 변환 의 과정을 잘 추적해 보면, u 와 v 는 주파수와 밀접하게 연관이 있다는 것은 부정할 수 없다. 본문에서 짧게 언급했듯 u, v 가 클수록 고주파 성분이라는 점은 확실하다.
여기까지 이해했다면, Shifting 이 하고자 하는 것을 살펴보자. DC 가 중심으로 왔을 뿐, 뒤죽박죽이 됐다.
해소되지 않는 의문 : 이거 왜 하는거임?
단지 사분면만 옮긴 것은 아닌 것 같은데... 뭔가 더 추가적인 알고리즘이 있나보다.