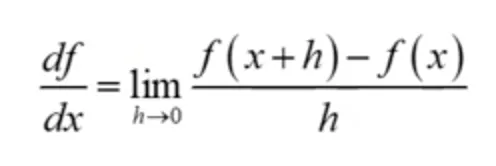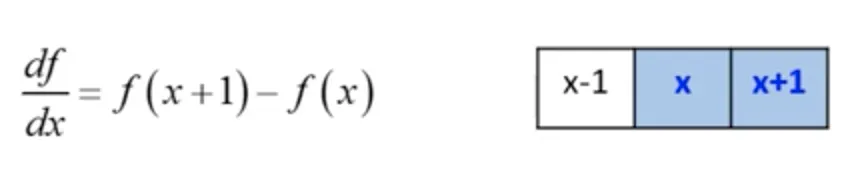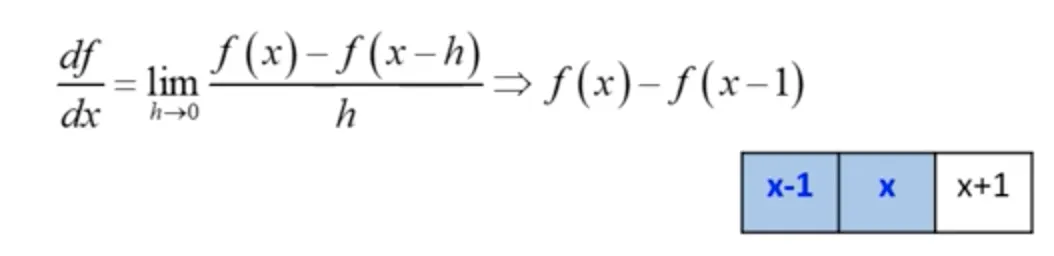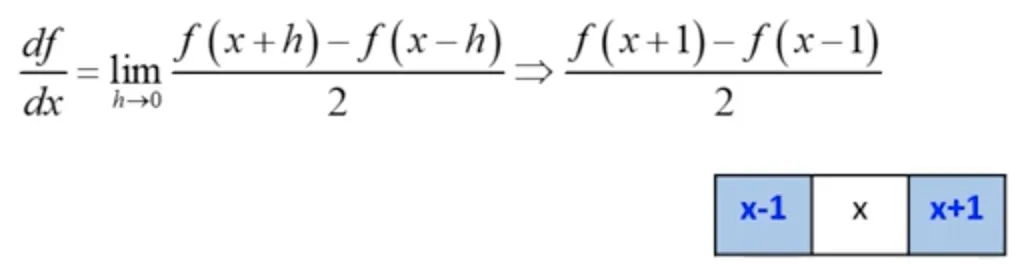Search
9️⃣

영상의 영역 분할 [2021/06/13]

영상의 영역 분할

영상의 영역 분할 (segmentation) 은 영상을 구성 요소로 혹은 분리된 물체로 구분하는 연산이다.
•
문턱치 처리 : thresholding
•
에지 검출 : edge edtection
이 강의에서는 고전적인 segmentation 방법들을 다룬다. 조금 더 다양한 방법들은 을 참고하자

문턱치 처리 (thresholding)

단일 문턱치 처리 (single thresholding)

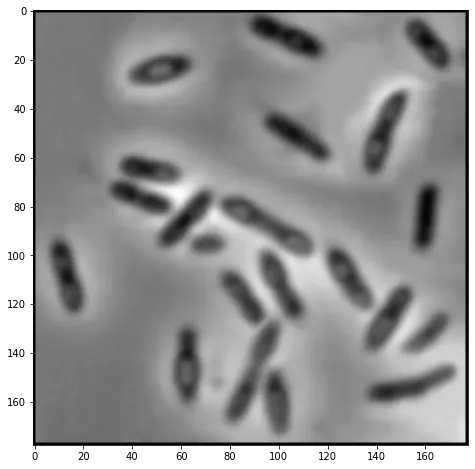
single thresholding 은 밝기값이 T 보다 큰 값은 흰색으로, 작은 값은 검은색으로 변경하여 binary image 로 만드는 알고리즘이다.
•
배경에서 영상을 분리하고 싶을 때
•
영상에서 육안으로는 잘 구분하지 못하는 외관을 보고 싶을 때
im = cv2.imread('bacteria.tif', cv2.IMREAD_GRAYSCALE) plt.figure(111, figsize = [8,8]) plt.imshow(im, cmap='gray')
Python
복사
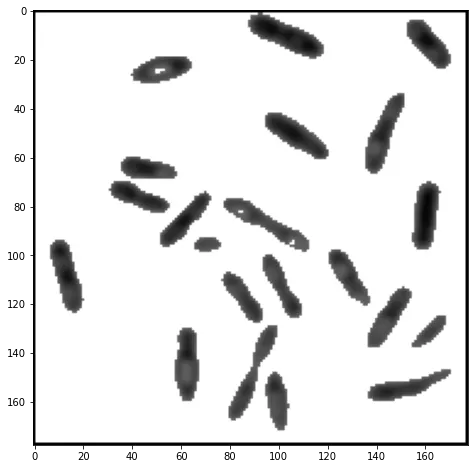
im[im > 100] = 255 plt.figure(112, figsize = [8,8]) plt.imshow(im, cmap='gray')
Python
복사

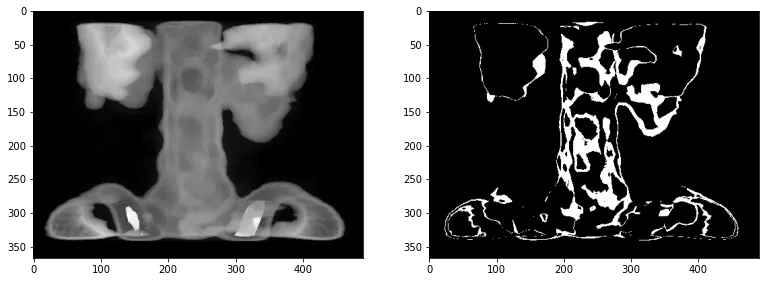
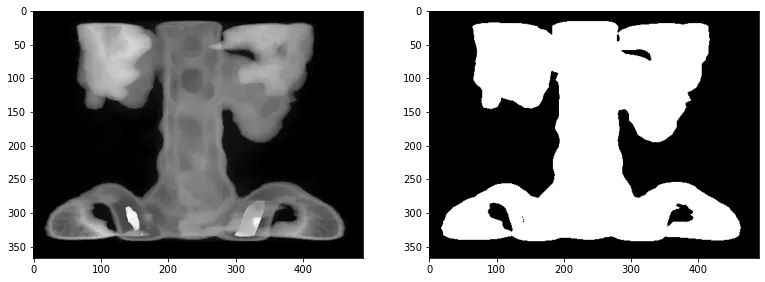
이중 문턱치 처리 (double thresholding)

im_spine = cv2.imread('spine.tif', cv2.IMREAD_GRAYSCALE) plt.figure(114, figsize = [13,5]) plt.subplot(1,2,1) plt.imshow(im_spine, cmap='gray') cond = (im_spine > 115) & (im_spine < 125) im_spine[cond] = 1 im_spine[~cond] = 0 plt.subplot(1,2,2) plt.imshow(im_spine, cmap='gray')
Python
복사

적절한 문턱치 설정

적절한 문턱치를 설정하기 위해 histogram 을 확인해보는 전략을 취할 수 있다.
im_conis = cv2.imread('coins.tif', cv2.IMREAD_GRAYSCALE) plt.figure(115, figsize = [13,5]) plt.subplot(1,2,1) plt.imshow(im_conis, cmap='gray') x_range = [0, 255] bins = 2**8 # 256 plt.subplot(1,2,2) plt.hist(im_conis.flatten(), bins=bins, range=x_range)
Python
복사
•
위 histogram 을 보면, 약 150 정도의 문턱지를 설정하면 좋을 것이다.
•
하지만, 이렇게 설정된 문턱치는 이 영상에 대해서 제한적이다.
•
매번 다른 영상이 들어오더라도 적절한 문턱치를 찾을 수 있도록 진화해야 한다.
영상의 histogram 을 확률분포로 모사한 뒤, 이 분포를 적절히 나눌 수 있는 문턱치를 가져가는 전략을 통해 자동으로 문턱치를 설정할 수 있지 않을까?

Otsu 의 방법론

•
class 는 종류를 의미하는 것으로, 배경과 물체를 나누는 segmentaiton 을 한다고 한다면, 배경과 물체가 각각 1개의 class 를 의미한다고 생각할 수 있다.
•
inter-class variance 는 서로 다른 class 간의 차이를 의미한다.
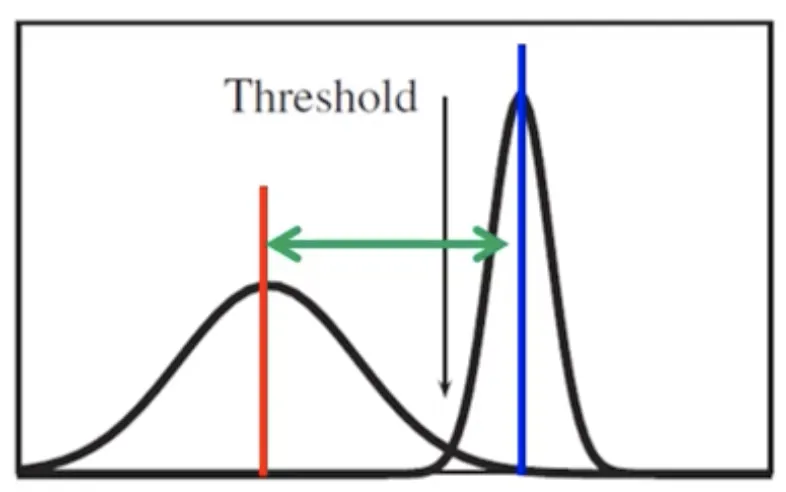
Otsu 의 방법은, Inter-class variance 를 최대화하는 문턱치를 찾는 방법이다.
위 그림을 보자. red : class 1 의 평균, blue : class 2 의 평균일 때, 이 두 class 를 가장 잘 구분할 수 있는 문턱치를 설정한다는 말이 된다.
그렇다면 class 간의 차이를 의미하는 inter-class variance 를 Otsu 는 어떻게 정의했을까?
•
문턱치 tt 가 변함에 따라서, t 보다 작은 영역에 속하는 확률분포가 class 0, t 보다 큰 영역에 속하는 확률분포가 class 1 에 속하는 확률분포 pp 라고 생각해 보자.
•
각 확률 분포의 평균 μ0,μ1{\mu}_0, {\mu}_1 을 구한다.
•
inter-class variance 는 각 확률 분포의 평균 차이의 제곱에 비례한다.
•
inter-class variance 는 각 클래스에 속할 확률의 곱에 비례한다.
f(t)=ω0(t)ω1(t)[μ0(t)−μ1(t)]2f(t)={\omega}_0(t){\omega}_1(t)[{\mu}_0(t)-{\mu}_1(t)]^2
수식을 바라보다 보니 문득 든 생각인데, 어차피 위 함수 f(t)f(t) 를 최대가 되도록 만드는 t 를 찾는 것이기 때문에, 식을 이렇게 변경해도 될 것 같았다. f(t)=(ω0(t)ω1(t))1/2{(μ0(t)−μ1(t))2}1/2f(t)=({\omega}_0(t){\omega}_1(t))^{1/2}\{({\mu}_0(t)-{\mu}_1(t))^2\}^{1/2} 식을 이렇게 변경하게 되면, t 가 갈라놓은 두 확률분포에서, 각 클래스에 해당하는 확률값의 (확률분포의 아래 면적) 기하평균에 비례하고, 두 확률분포의 평균의 차이에 비례하는 어떤 함수를 가장 크게 만드는 t 를 찾는 문제라고 해석할 수 있게 된다.
def otsu(im): t = 0 max_f = 0 for i in range(1, 256): cond = im < i x1 = im[cond] x2 = im[~cond] if len(x1) == 0: continue if len(x2) == 0: continue mu1 = x1.mean() mu2 = x2.mean() _, x1_counts = np.unique(x1, return_counts=True) _, x2_counts = np.unique(x2, return_counts=True) p1 = sum(x1_counts) p2 = sum(x2_counts) f = p1*p2*(mu1-mu2)**2 if max_f < f: max_f = f t = i return t def auto_thresholding(im, return_threshold=False): im = im.copy() t = otsu(im) cond = (im > t) im[cond] = 1 im[~cond] = 0 if return_threshold: return im,t else: return im plt.figure(116, figsize=[13,5]) plt.subplot(1,2,1) plt.imshow(im_conis, cmap='gray') ret, threshold = auto_thresholding(im_conis, return_threshold=True) print("Thresholding with Otsu's method:", threshold) plt.subplot(1,2,2) plt.imshow(ret, cmap='gray')
Python
복사
물론 이렇게 구현해 쓰는 건 병렬처리와 연산 최적화가 되지 않기 때문에 느리고 성능도 별로다.
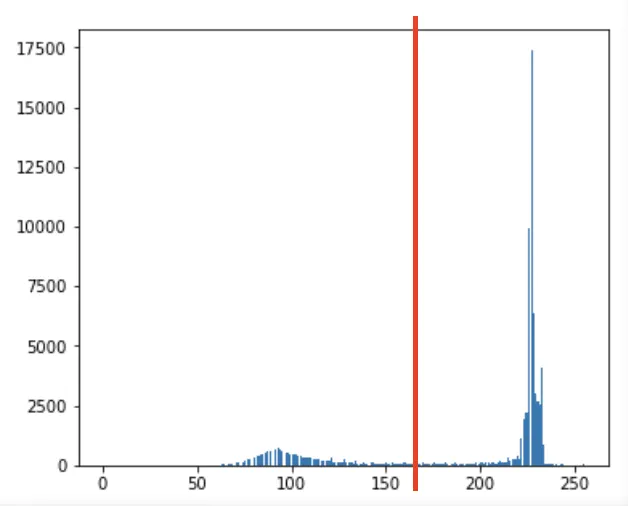
Thresholding with Otsu's method: 166
Plain Text
복사
잘 - 찾았다!
plt.figure(117, figsize=[13,5]) plt.subplot(1,2,1) im_spine = cv2.imread('spine.tif', cv2.IMREAD_GRAYSCALE) plt.imshow(im_spine, cmap='gray') ret, threshold = auto_thresholding(im_spine, return_threshold=True) print("Thresholding with Otsu's method:", threshold) plt.subplot(1,2,2) plt.imshow(ret, cmap='gray')
Python
복사
Thresholding with Otsu's method: 64
Plain Text
복사
plt.figure(117, figsize=[13,5]) plt.subplot(1,2,1) x_range = [0, 255] bins = 2**8 # 256 plt.hist(im_spine.flatten(), bins=bins, range=x_range) plt.subplot(1,2,2) x_range = [0, 255] bins = 2**8 # 256 plt.hist(im_spine[im_spine < threshold].flatten(), bins=bins, range=x_range, color='r') plt.hist(im_spine[im_spine >= threshold].flatten(), bins=bins, range=x_range, color='b')
Python
복사

적응형 문턱치 처리

적응형 문턱치 처리가 필요한 상황을 임의로 생성해 보자.
from mpl_toolkits.mplot3d import axes3d plt.figure(211, figsize=[13,5]) # --- plt.subplot(1,2,1) im_circles = cv2.imread('circles.tif', cv2.IMREAD_GRAYSCALE) plt.imshow(im_circles, cmap='gray') # --- plt.subplot(1,2,2) im_circles_noised = np.ones(im_circles.shape) noise = np.linspace(0,im_circles.shape[-1]-1,im_circles.shape[-1])/2 mask = (im_circles == 0) im_circles_noised[mask] = (im_circles_noised * noise)[mask] noise = np.linspace(0,im_circles.shape[-1]-1,im_circles.shape[-1])/2+50 im_circles_noised[~mask] = (im_circles_noised * noise)[~mask] im_circles_noised = im_circles_noised.astype(np.uint8) plt.imshow(im_circles_noised, cmap='gray')
Python
복사
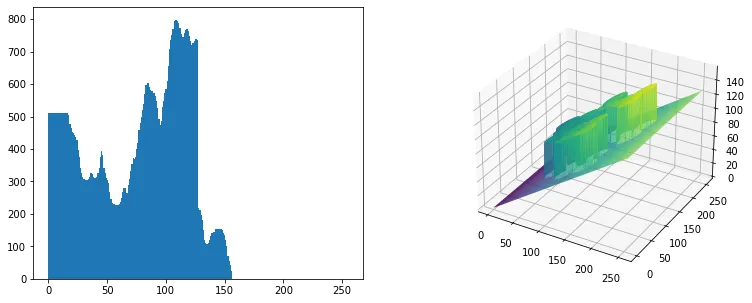
plt.figure(212, figsize=[13,5]) # --- plt.subplot(1,2,1) x_range = [0, 255] bins = 2**8 # 256 plt.hist(im_circles_noised.flatten(), bins=bins, range=x_range) # --- ax = plt.subplot(1,2,2, projection='3d') X = np.linspace(0, im_circles_noised.shape[1]-1, im_circles_noised.shape[1]).astype(np.uint8) Y = np.linspace(0, im_circles_noised.shape[0]-1, im_circles_noised.shape[0]).astype(np.uint8) X, Y = np.meshgrid(X, Y) ax.plot_surface(X, Y, im_circles_noised, rstride=1, cstride=1,cmap="viridis")
Python
복사
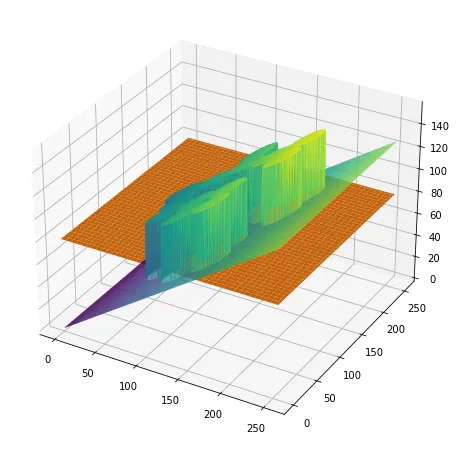
이런 상황에서, 단일 문턱치를 이용해 segmentation 하겠다는 것은 아래 코드와 같은 상황을 나타낸다.
plt.figure(212, figsize=[8,8]) ax = plt.subplot(1,1,1, projection='3d') X = np.linspace(0, im_circles_noised.shape[1]-1, im_circles_noised.shape[1]).astype(np.uint8) Y = np.linspace(0, im_circles_noised.shape[0]-1, im_circles_noised.shape[0]).astype(np.uint8) X, Y = np.meshgrid(X, Y) ax.plot_surface(X, Y, im_circles_noised, rstride=1, cstride=1,cmap="viridis") t = 80 t_surface = np.ones(im_circles_noised.shape)*t ax.plot_surface(X, Y, t_surface)
Python
복사
영상을 작은 부분으로 나누고, 각각에 대하여 문턱치 처리를 해 보는 방법을 생각해 볼 수 있다.
plt.figure(213, figsize=[8,8]) plt.subplot(1,2,1) trial_1 = auto_thresholding(im_circles_noised) plt.imshow(trial_1, cmap='gray') plt.subplot(1,2,2) trial_2_1 = auto_thresholding(im_circles_noised[:,:50]) trial_2_2 = auto_thresholding(im_circles_noised[:,50:100]) trial_2_3 = auto_thresholding(im_circles_noised[:,100:150]) trial_2_4 = auto_thresholding(im_circles_noised[:,150:256]) plt.imshow(np.concatenate([trial_2_1, trial_2_2, trial_2_3, trial_2_4], axis=1), cmap='gray')
Python
복사
좌측은 단순히 Otsu 의 방법을 사용했을 경우이고
우측은 네 영역으로 분할한 뒤 각각에 Otsu 의 방법을 적용한 경우이다.
이런 방법들 외에도, 정말 다양한 아이디어를 낼 수 있을 것이라고 짐작할 수 있다. 이 강의에서는 segmentation 에 대해서 여기까지만 다룬다. 앞으로 나올 edge detection 에서도 너무 깊이 들어가지 않고 가볍게 다룬다.

에지 검출 (edge detection)

에지 (edge) 는 주어진 문턱치를 초과하는 픽셀값들의 국부적인 불연속을 의미한다. 경사 에지 (ramp edge) 는 밝기값이 서시히 변하는 에지를 의미한다. 계단 에지 (step edge) 는 밝기값이 급격히 변하는 에지를 의미한다.

프로파일 (profile) 과 미분 (derivative)

프로파일 (profile) 은 어떠한 변화를 의미한다.
어떤 미분가능한 함수에서 도함수는 아래와 같이 표현한다.
그런데 영상에서 가장 작은 변화의 단위는 1 이다.
이것을 조금만 더 확장해서 생각해서, 최소단위가 2라고 생각해도 무리가 없다.

기울기 (gradient) 와 편미분 (partial derivative)

기울기 (gradient) 는 함수 f(x,y) 에 대해서 밝기값이 증가하는 방향의 벡터이다.
사실 꼭 증가하는 방향으로 정의할 필요는 없는 것 아닐까. 하지만 이렇게 약속함으로써, 오른쪽과 윗쪽은 항상 +, 왼쪽과 아랫쪽은 항상 - 모양의 필터들만 찾을 수 있게 되었다. 그리고 오른쪽과 윗쪽의 f(x+h) 에서 왼쪽과 아랫쪽의 f(x-h) 를 빼 주는 형태가 되었다. 이렇게 된다면 연산의 결과가 반드시 밝기값이 증가하는 방향의 벡터만 나오게 된다. 이렇게 무엇인가를 관례적으로 약속해두면 생각이 상당히 간단해지곤 한다.

에지 검출 필터

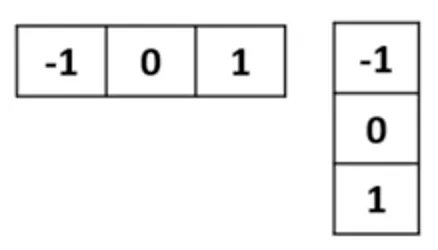
f(x+1)−f(x−1)f(x+1)-f(x-1) 을 도함수로 여기고 필터로 만들면 된다.
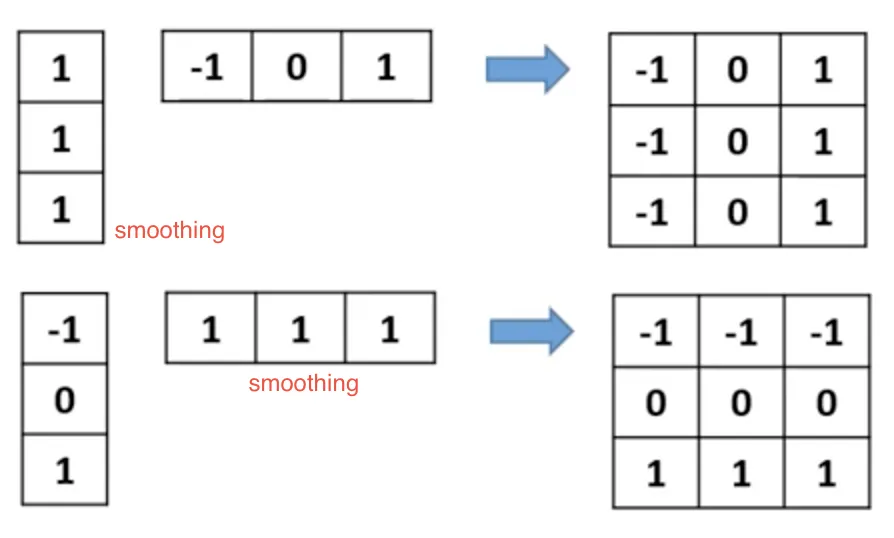
그런데 여기서 검출하려는 방향의 반대 방향으로 복사-붙여넣기 한 형태의 필터는 smoothing 의 역할을 한다. 앞서 영역 단위 영상처리 연산과 필터링 과 영상의 열화와 복원 에서 배웠듯, 커널 (필터) 의 사이즈가 커지면 국소적인 노이즈에 강인해지지만 디테일이 사라지는 등의 문제가 있었던 것을 기억하자.
이렇게 생긴 filter 들을 Prewitt filter 이라고 한다.
Prewitt operator - Wikipedia
The Prewitt operator is used in image processing, particularly within edge detection algorithms. Technically, it is a discrete differentiation operator, computing an approximation of the gradient of the image intensity function. At each point in the image, the result of the Prewitt operator is either the corresponding gradient vector or the norm of this vector.
https://en.wikipedia.org/wiki/Prewitt_operator
좌측 : 원본, 중앙 : x 방향 에지 검출기, 우측 : y 방향 에지 검출기
x 방향 에지 검출기가 만든 결과를 가까이서 들여다 보자. 위 이미지 조각처럼 경계에서는 "픽셀값이 밝아지는 방향" 이 다르기 때문에, 에지 검출기로부터 나타나는 밝기값이 완전히 반대이곤 하다. (하양, 검정).
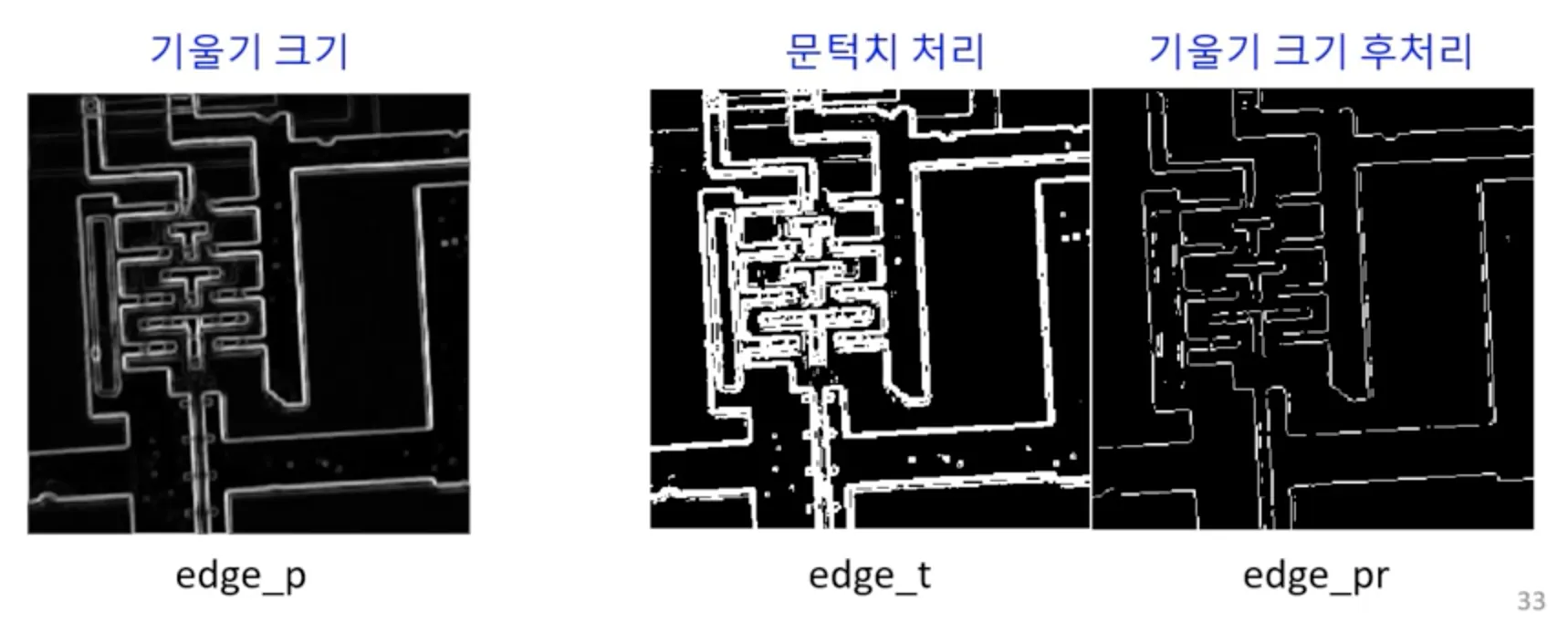
기울기의 크기를 구하는 연산을 거치면 edge_p 가 된다. 그리고 threshold 를 이용해서 일정한 기준으로 에지인 것과 아닌 것을 구분해 주면 edge_t 의 결과를 얻을 수 있다.
추가 자료
이장후_seminar2_image filtering and convolution.pdf
4791.4KB