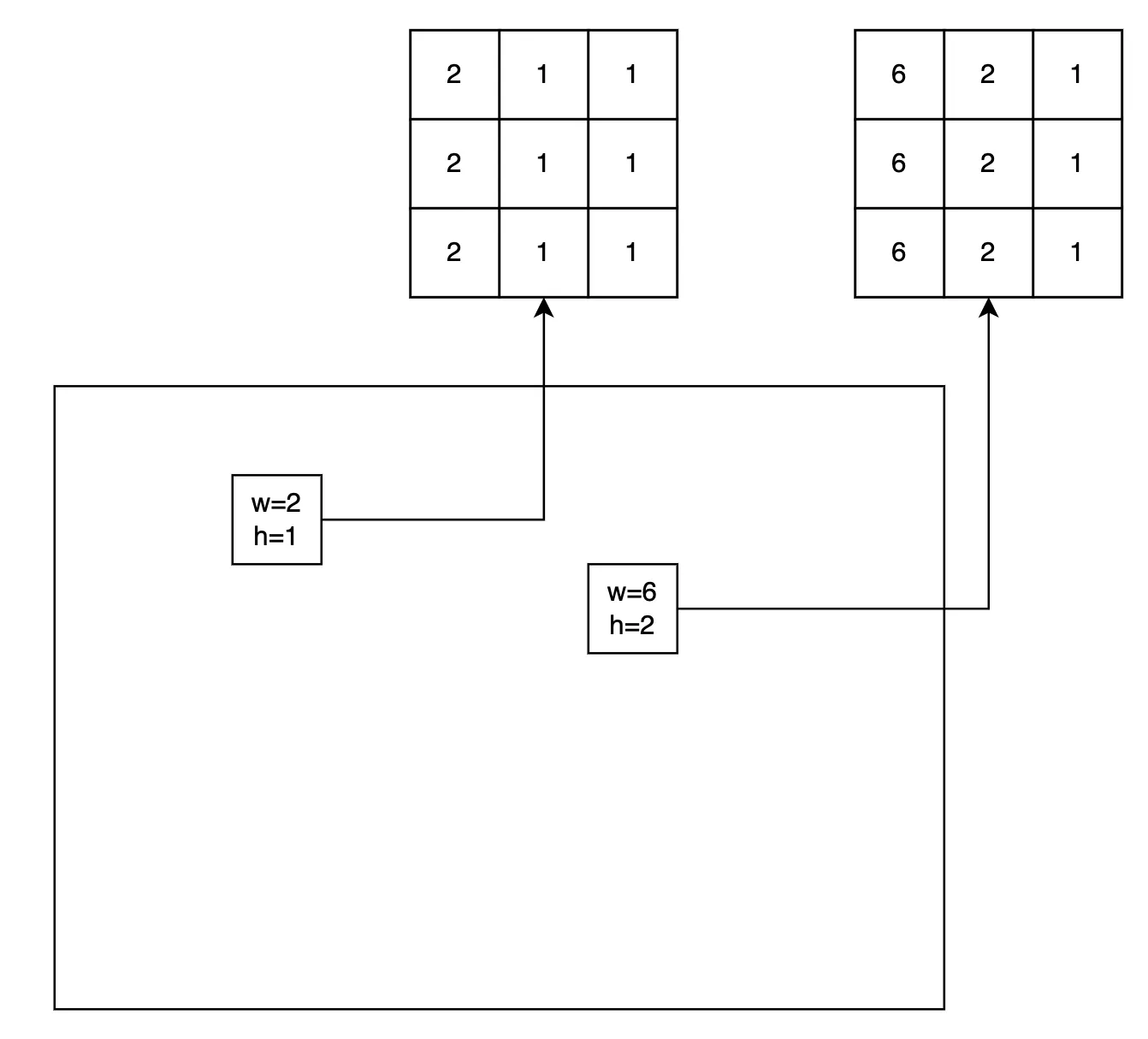
각 채널의 값 범위가 인 homogeneous coordinate meshgrid 가 있다. 이 격자의 회전 후 좌표값을 구하고 싶어서 인 rotation matrix 를 곱하고자 하는 상황을 상상해 보자.
이 과정을 TensorFlow 또는 numpy 에서 처리하기 위해 에 dummy dimension 을 추가해 형태로 바꾸고 과 elementwise multiply 를 취하도록 할 수 있다. 이렇게 하면 브로드캐스팅이 일어나며, 이라는 연산이 일어나게 된다. 그런데 여기서 머리가 지끈지끈해진다. 3차원을 초과해 버린 텐서이기 때문이다. 인간은 태생적으로 이것을 직관적으로 이해할 수 없다. 이것을 어떻게 해석할 수 있을까?
예제는 (참고1) 로부터 가져왔다.
그냥 행렬의 가장 구체적인 차원, 즉 끝단만 생각해 본다. 맨 마지막 두 개 차원만 똑 떼어내면 어떻게 생겼을까?
[[2, 5, 1],
[2, 5, 1],
[2, 5, 1],]
Python
복사
뭐 이렇게 생겼을것이다. 위 자료구조 각각의 값이 무엇을 나타내는지 잘 생각해 보자.
step1
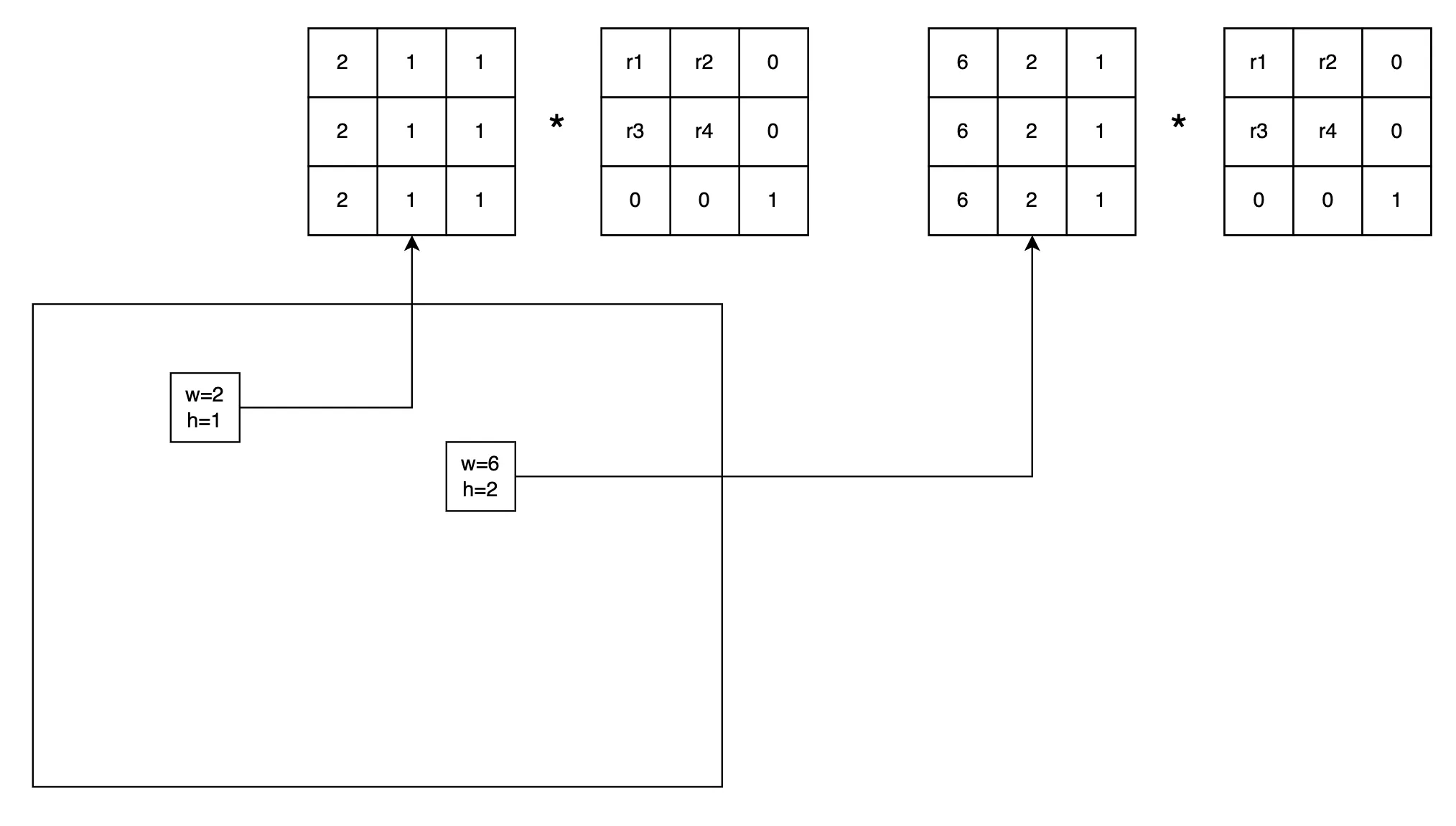
여기에 rotation 행렬을 곱해 준다는 것이 어떤 의미를 지니는지 이해해 본다. 아참 행렬곱이 아니라 elementwise multiply 이다! 행렬곱을 모사하는거다. dot product 과 비슷하지만 곱셈 후 sum 을 하지는 않을 것이다.
[[r1, r2, 0],
[r3, r4, 0],
[ 0, 0, 1],]
Python
복사
그 결과가 어떻게 나올까.
step2
연산을 하는 과정은 위 그림처럼 상상해 볼 수 있다. 그리고 이러한 형태가 의 형태에 맞추어 쭉~ 타일처럼 붙어 있다고 생각하면 된다. 여기까지 이해됐다면 다음 과정은 뻔하다. 이 과정이 무슨 의미를 가질까? 그냥 행렬 곱을 해 주고 싶은데, 행렬 곱을 하기 어려우니까 브로드캐스팅으로 복제하고 elementwise 연산을 한 뒤 Rotation 행렬과 각 meshgrid 의 픽셀마다 연산해서 모든 픽셀의 회전 후의 좌표를 얻고자 하는 과정의 일부일 뿐이다. 그럼 reduce_sum 같은 연산을 통해 행 방향으로 연산 결과를 합해주고, 더미 차원은 없애주는 과정이 다음에 붙어야 한다는 사실을 바로 받아들일 수 있다.
코드 (참고1)
pixel_directions = pixel_directions[..., None, :] # (w, h, 1, 3)
ray_directions = tf.math.multiply(pixel_directions, camera_rotation) # (w, h, 3, 3)
ray_directions = tf.reduce_sum(pixel_directions, axis=-1) # (w, h, 3)
Python
복사
이를 코드 세 줄로 적을 수 있다.
이 설명에서는 ‘가장 낮은 차원의’ 구체적인 케이스 하나를 이해하고 의미를 곱씹어본 뒤, 얻은 의미를 ‘너비(w) 와 높이(h) 라는 좋은 틀을 사용해서’ 귀납적 직관을 이용해 확장해 나가 전체의 맥락에서 다시 의미를 찾았다. 추상적인 정보를 이해하는 원칙이 그대로 적용됐다 (참고2).
참고
1.