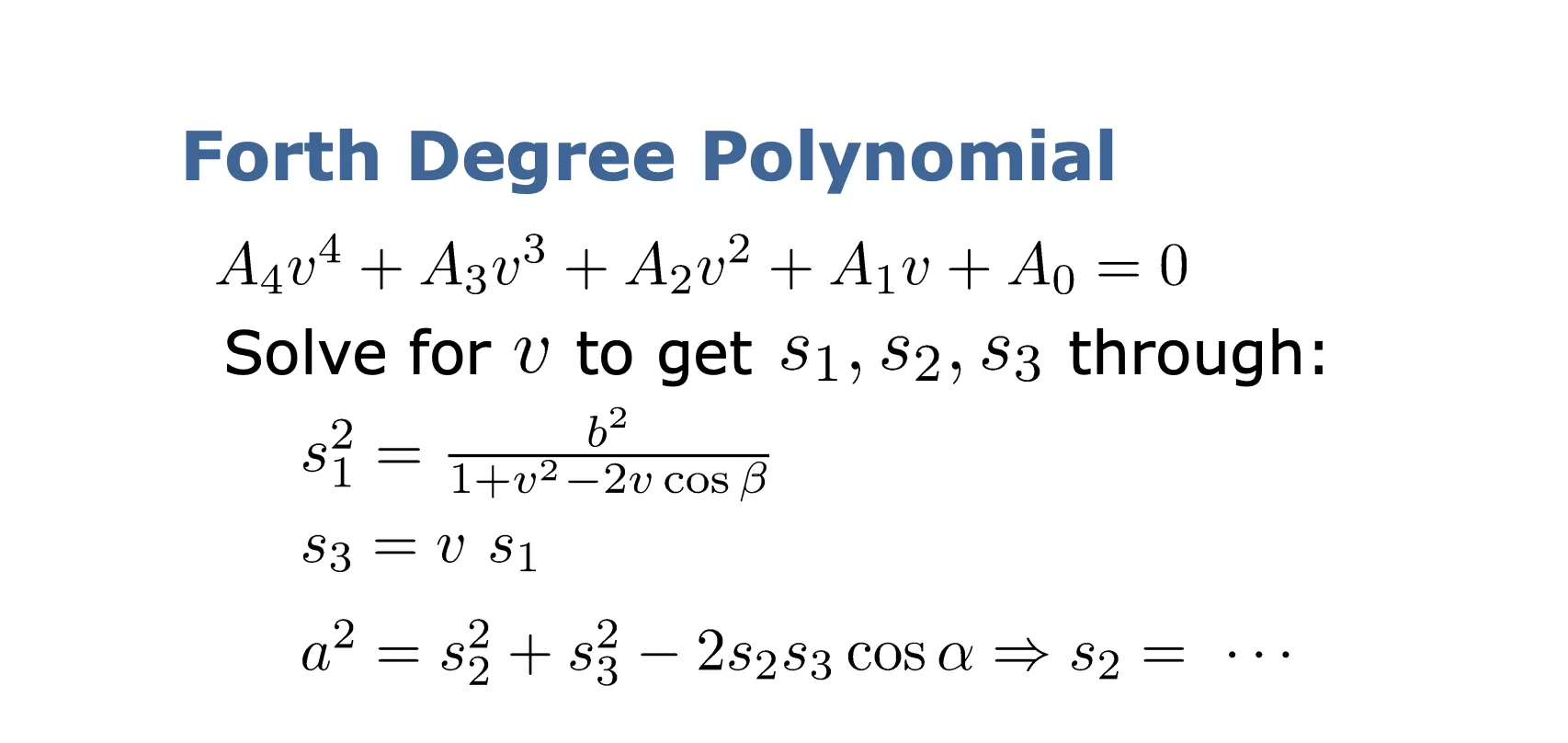Search
🔵

b3.4_5.3. title: 캘리브레이션(‣)된 카메라에 대해서 P3P(‣)로 카메라의 포즈를 추정할 수 있다.

생성
🚀 prev note
♻️ prev note
🚀 next note
14 more properties
sis_i와 XOX_O를 구하기 위한 머나먼 여정을 떠난다. 우선 벡터의 내적을 이용하여 각도를 구한다. α,β,γ{\alpha},{\beta},{\gamma} 는 모두 실수 값으로 알려져 있는 값이다.
P3P 는 직접 해결 방법(‣ Direct solution)의 일종으로(sup1), 위 그림의 sis_i와 XOX_O를 구하는 로컬라이제이션(localization) 문제다.
si kxis=R(Xi−XO), i=1,2,3s_i{~^k{\mathrm{x}^s_i}}=\mathrm{R}(X_i-X_O),\ i=1,2,3
해석 순서
의미
알려짐 여부
1
 kxis{~^k{\mathrm{x}^s_i}}
카메라 원점 좌표계의 언어로 해석한 카메라 원점 XOX_O에서부터 카메라 원점 좌표계의 언어로 해석한 월드 좌표 XiX_i로 향하는 방향의 단위벡터(direction unit vector). kk는 캘리브레이션을 통해 카메라 내부 파라미터를 모두 알고 있음을 의미함,
known
2
sis_i
단위벡터  kxis{~^k{\mathrm{x}^s_i}} 의 스케일
unknown
3
si kxiss_i{~^k{\mathrm{x}^s_i}}
카메라 원점이 시점이고 점 XiX_i이 종점인 벡터를 카메라 원점 좌표계의 언어로 해석한 벡터
unknown
4
Xi−XOX_i-X_O
월드 좌표계의 언어로 해석한 카메라 원점 XO\mathrm{X}_O에서부터 월드 좌표계의 언어로 해석한 월드 좌표 XiX_i로 향하는 방향과 크기를 가진 벡터
XOX_O: unknown XiX_i: known
5
R\mathrm{R}
월드 좌표계와 카메라 좌표계의 변환을 모델링하는 회전 변환 행렬
unknown
우리는 P3P 문제를 풀 때, 카메라 캘리브레이션이 완료되어 있다고 전제한다. 또한 이는 로컬라이제이션 목적으로 만들어진 알고리즘이므로, 월드 좌표계의 언어로 해석한 월드 좌표값을 의미하는 XiX_i를 알고 있음을 전제한다. 따라서 우리는 kxis{~^k{\mathrm{x}^s_i}}을 알고 있다.  kxis{~^k{\mathrm{x}^s_i}}는 다음과 같이 표현할 수 있다.
 kxis=−sign(c)N(K−1xi){~^k{\mathrm{x}^s_i}}=-\mathrm{sign}(c)\mathrm{N(K^{-1}x}_i)
해석 순서
의미
알려짐 여부
1
xi\mathrm{x}_i
카메라 원점 좌표계의 언어로 해석한 카메라 원점에서 이미지 좌표계의 언어로 해석한 이미지 평면 위의 점으로 향하는 크기와 방향을 가진 벡터
known
2
K−1xi\mathrm{K^{-1}x}_i
카메라 원점 좌표계의 언어로 해석한 카메라 원점에서 카메라 원점 좌표계의 언어로 해석한 정규 이미지 평면 위의 점으로 향하는 크기와 방향을 가진 벡터
known
3
N(v)\mathrm{N(v)}
길이가 1인 단위벡터로 만들어주는 함수
known
4
cc
카메라 상수(constant), 카메라 원점과 이미지 평면 사이의 거리. c는 카메라 원점과 이미지 센서 사이의 거리를 의미한다. 그런데 이 거리는 보통 카메라 렌즈와 카메라 원점의 반대 방향을 양의 방향으로 표현하곤 함. 따라서 이 값은 음수가 될수도 있음. sign\mathrm{sign}은 이를 보정하기 위해 존재
known
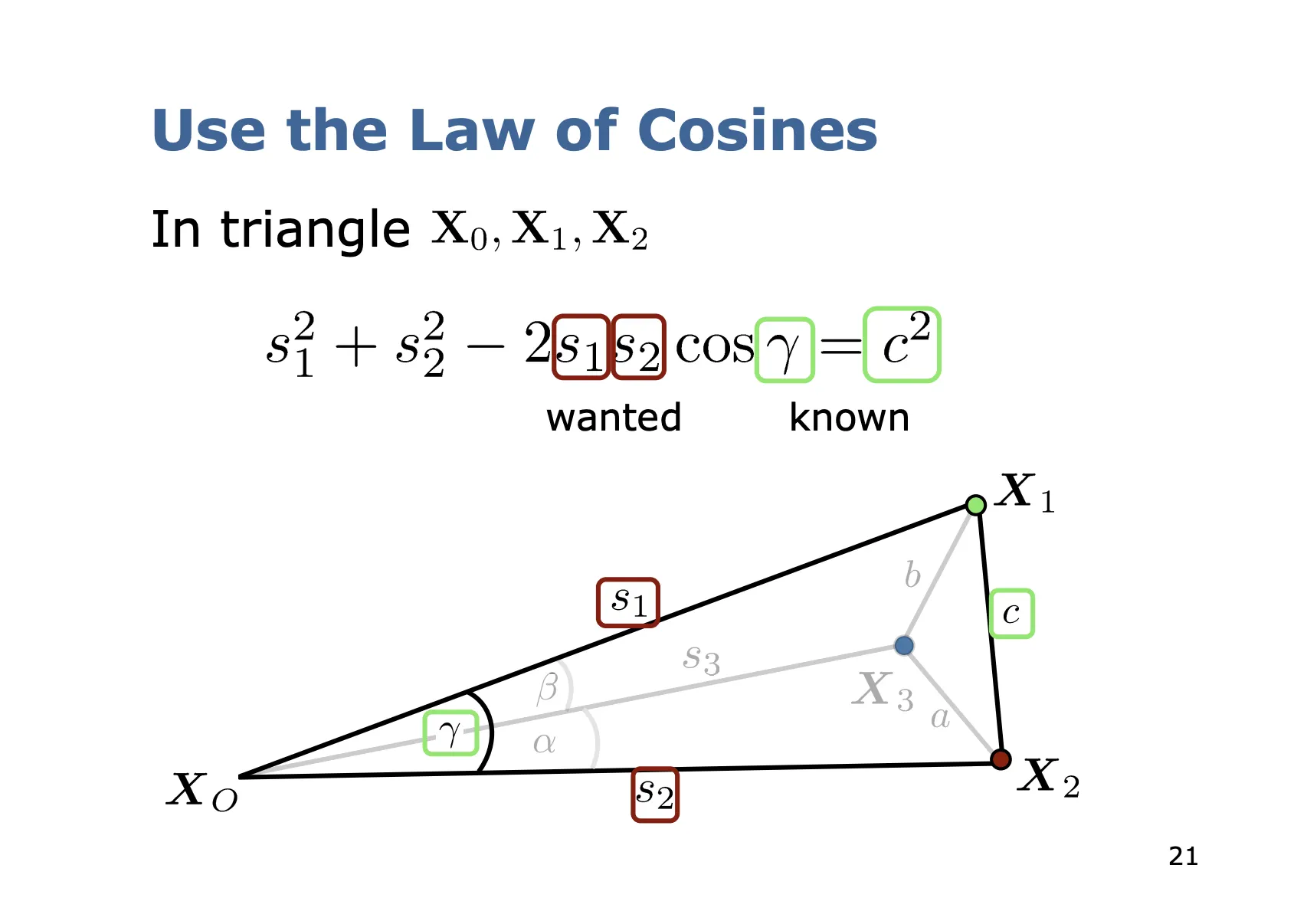
아래부터는 이 식을 풀어 나가는 과정이다.
코사인 법칙을 이용하여 s1,s2s_1, s_2 (모르는 값) γ{\gamma} (내적을 통해 구한 각도값) cc (처음부터 알고 있었던 카메라 상수) 사이 관계식을 세운다. 이를 a,ba,b 에 대해서도 당연히 똑같이 적용한다.
식 정리의 편의를 위해 u,vu,v 를 만들고 이를 이용해 식을 다시 쓴다.
변수는 u,vu,v 이지만 관계식이 두 개이므로 (첫번째 식=두번째 식, 두번째 식=세번째 식), u,vu,v 둘 중 하나를 남기고 정리할 수 있다.
ApA_p 는 모두 알려진 수들만으로 구성되어 있다.
4차방정식을 정리하면, vv 를 얻을 수 있고, vv 를 얻을 수 있으면 s1,s2,s3s_1, s_2, s_3 를 모두 구할 수 있다.
s1,s2,s3s_1, s_2, s_3 를 모두 얻었다면, 맨 처음 식을 다시 살펴보자.
si kxis=R(Xi−XO), i=1,2,3s_i{~^k{\mathrm{x}^s_i}}=\mathrm{R}(X_i-X_O),\ i=1,2,3
si kxiss_i{~^k{\mathrm{x}^s_i}}는 점 XiX_i을 카메라 원점 좌표계의 언어로 해석한 좌표값이라고 했다. si kxiss_i{~^k{\mathrm{x}^s_i}}와 XiX_i 를 알고 있다. 점이 3개 있으므로 관계식은 6개, 구해야 하는 파라미터가 6개이므로 회전변환행렬 R\mathrm{R}과 XOX_O를 구할 수 있다. 이를 연산하는 과정은 추후 서술하도록 하겠다.
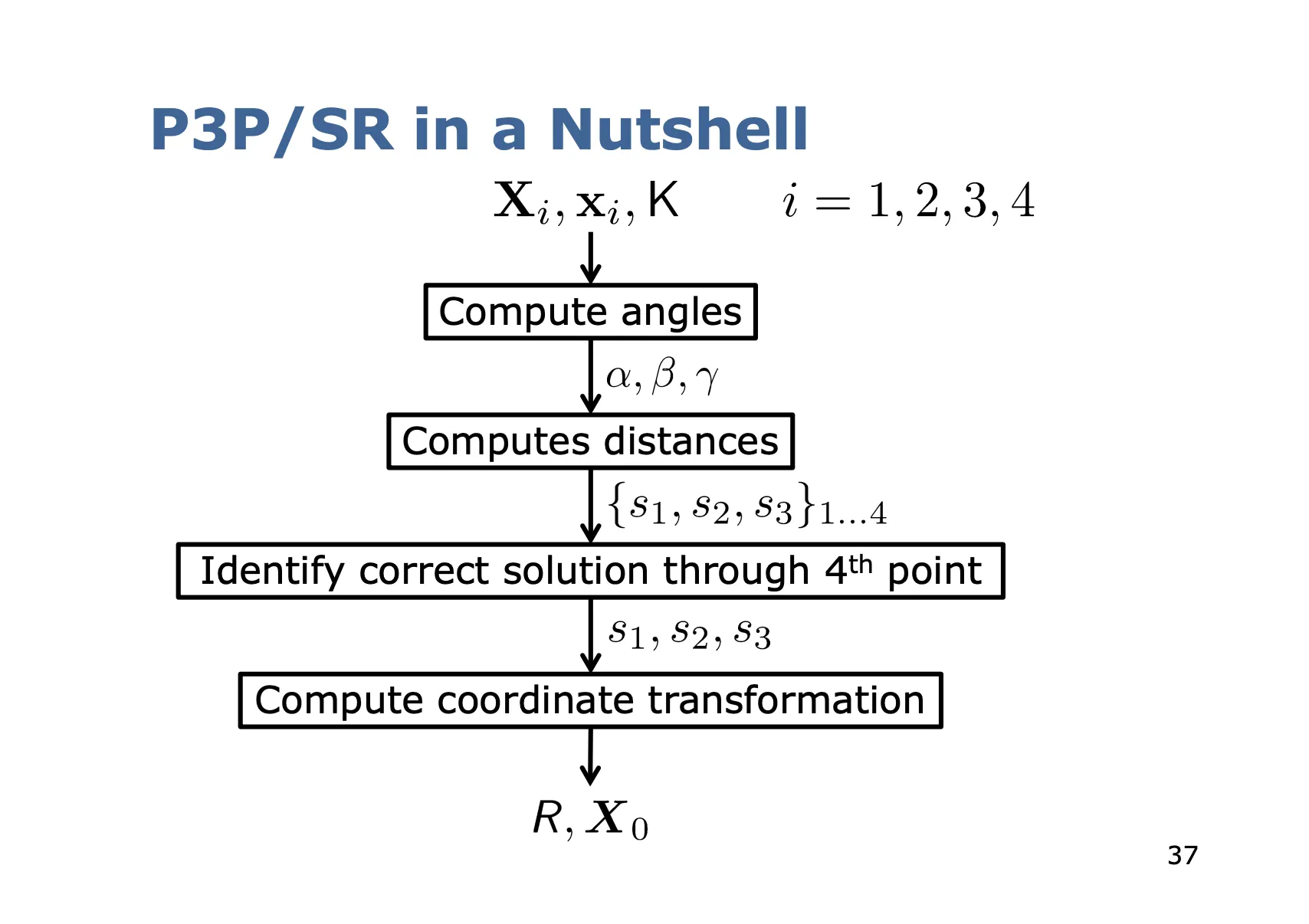
전체적인 파이프라인
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료들.
1.
P3P 이후의 연구들
from : 과거의 어떤 생각이 이 생각을 만들었는가?
1.
None
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는가?
1.
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는가?
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되고 이어지는가?
1.
참고 : 레퍼런스
1.
None