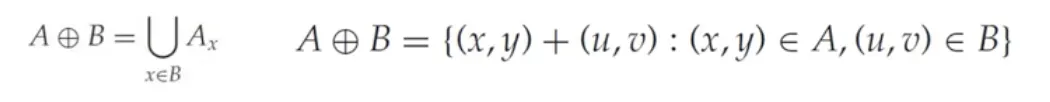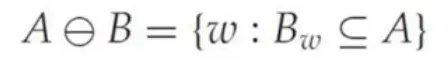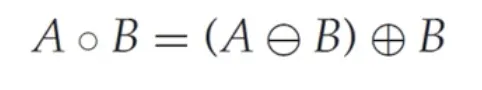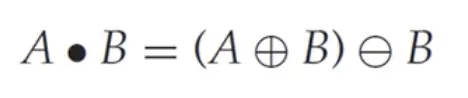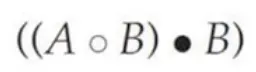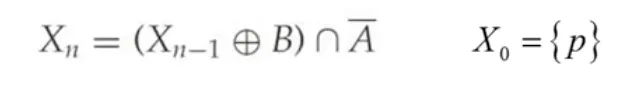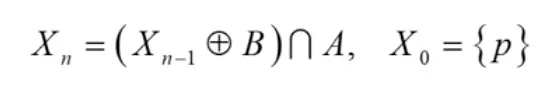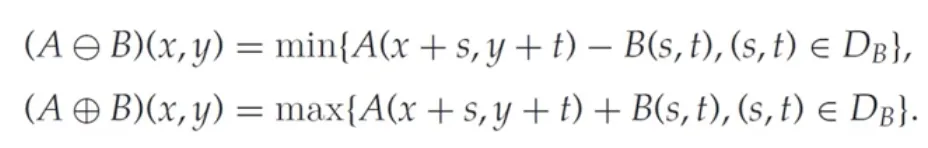영상의 형태적 처리
영상의 형태학 (morphology) 은 영상에서 형태를 분석하는 방법에 대한 분야를 의미한다.
생각의 단순화를 위해, Binary 영상에 대해서 먼저 다양한 형태적 처리를 해 보고, 그것을 Grayscale 로 확장시켜서 생각해보도록 하자.
기본 연산들
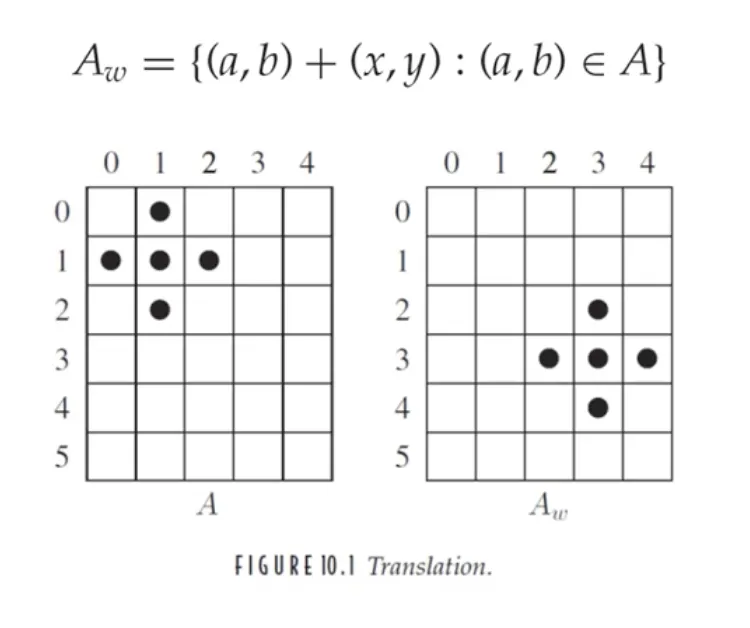
이동 (translation)
•
A 는 이진 (binary) 영상 화소들의 집합이다.
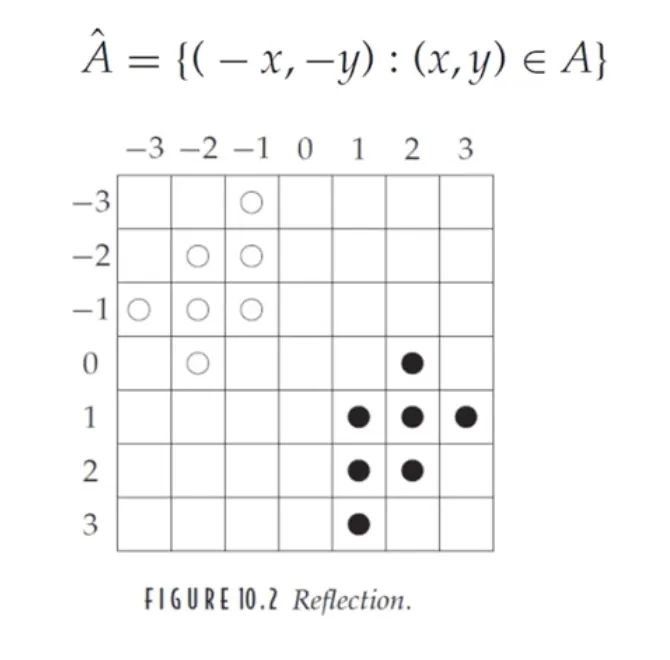
반사 (reflection)
•
A 는 이진 (binary) 영상 화소들의 집합이다.
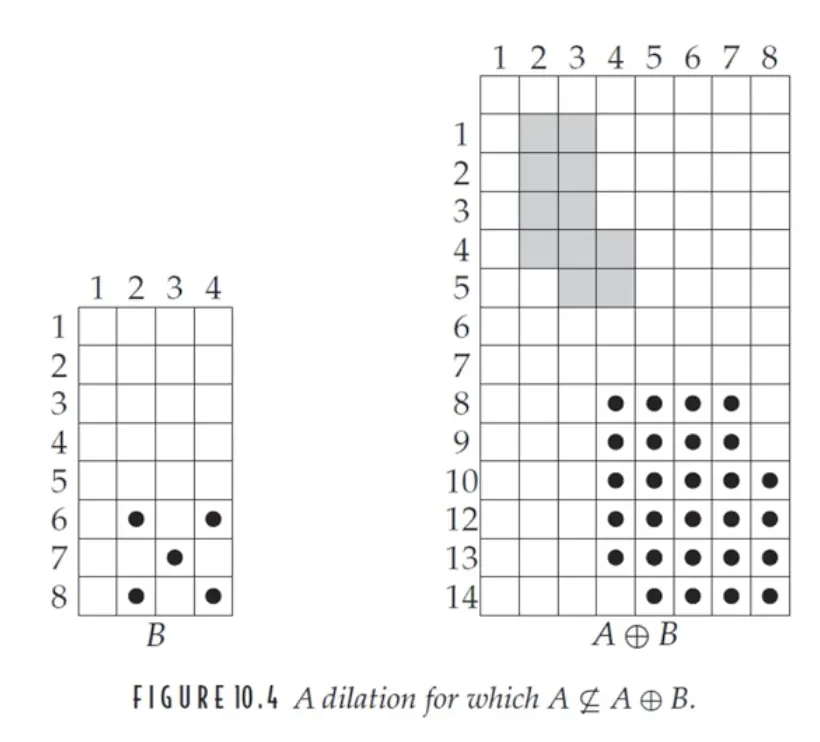
팽창 (dilation)
•
A 와 B 는 이진 (binary) 영상 화소들의 집합이다.
•
B 에 의한 A 의 팽창을 정의한다.
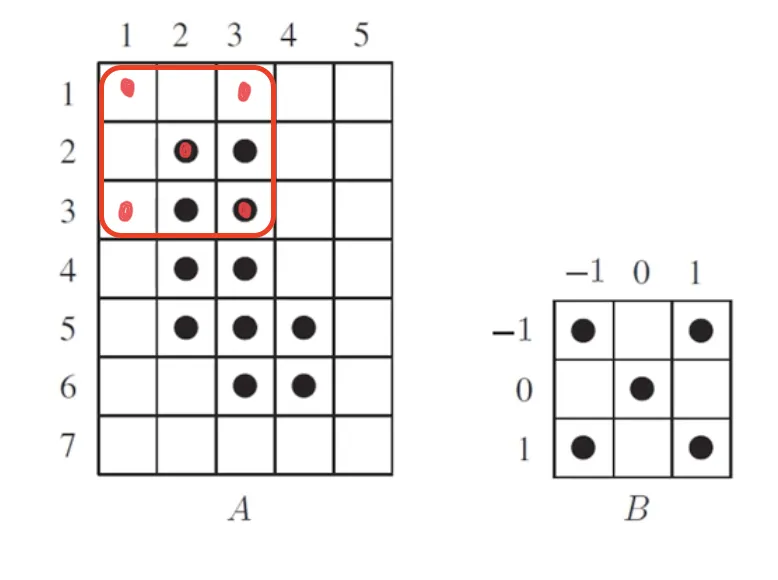
이것을 정확히 표현하면, "A 의 모든 화소 (x,y) 를 B 에 대한 사본으로 치환하여 합한다." 가 된다.
하는 역할의 느낌은 마치 A 가 원본 이미지, B 는 공간 필터처럼 느껴진다.
아래와 같은 괴상한 결과도... 정의에 따르면 팽창이다.
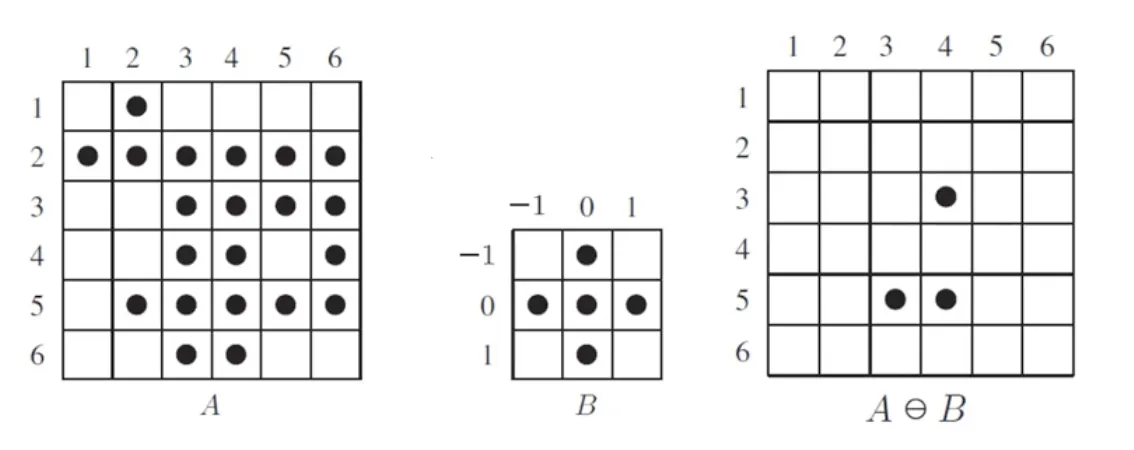
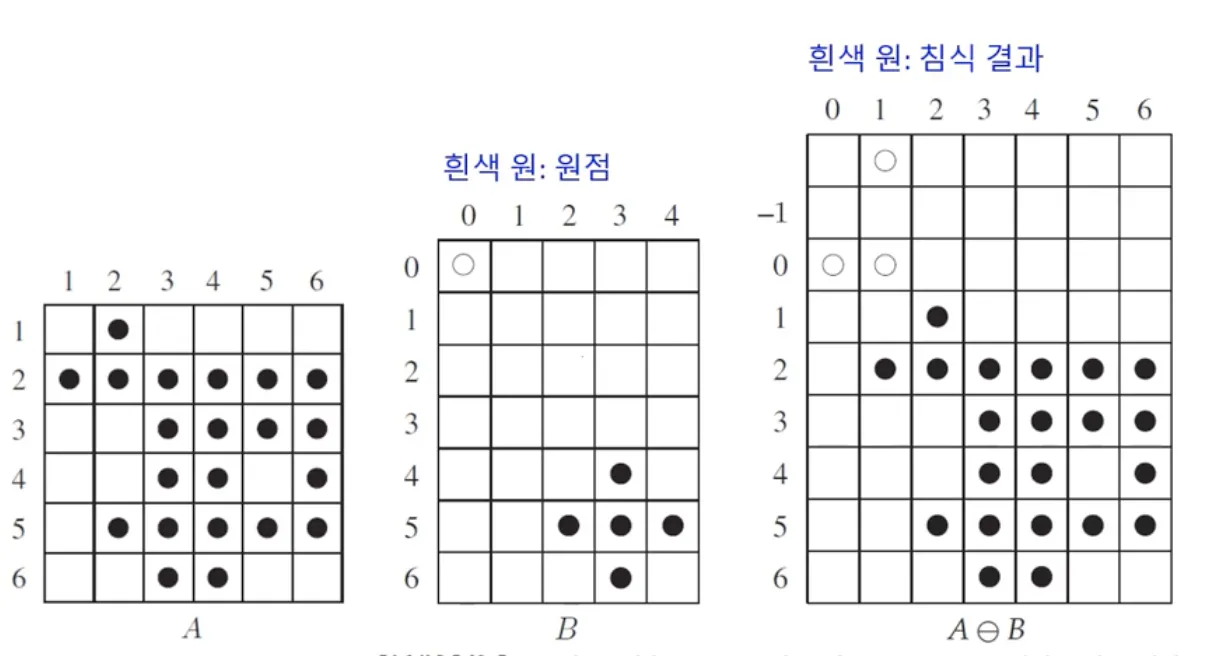
침식 (erosion)
•
A 와 B 는 이진 (binary) 영상 화소들의 집합이다.
•
B 에 의한 A 의 침식을 정의한다.
이것을 정확히 표현하면, "B 를 A에서 이동하며, B 가 A 의 내부에 완전히 속할 때에 B 의 원점 (0,0) 위치에 1 을 표기한다." 가 된다.
B 를 보면 영상의 중앙이 0,0 이다.
아래와 같은 괴상한 결과도... 정의에 따르면 침식이다.
이것은 원점을 어디에 두느냐에 대한 제약이 없기 때문에 생기는 결과물이다.
B 의 좌상단이 0,0 이다.
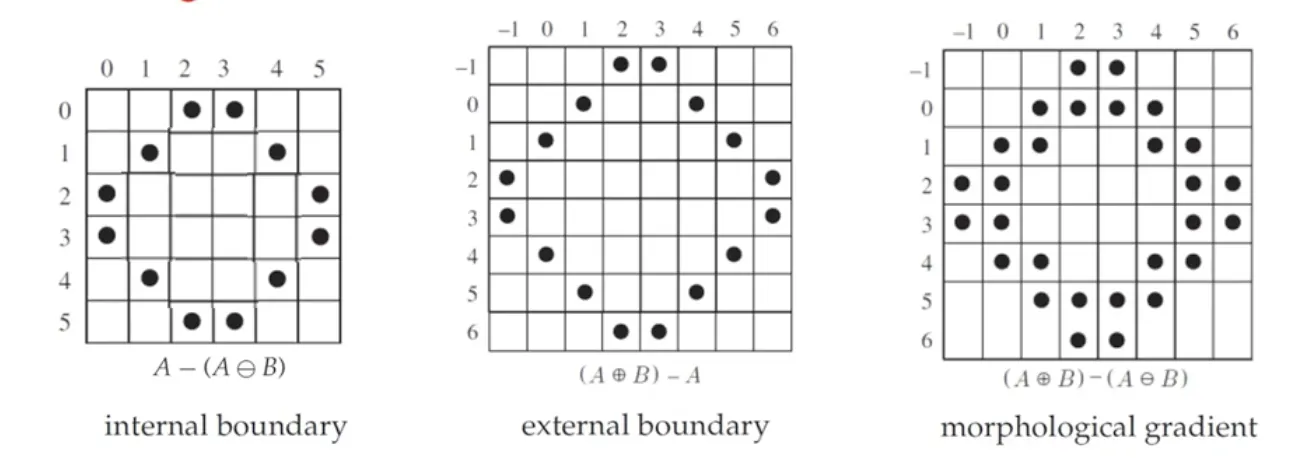
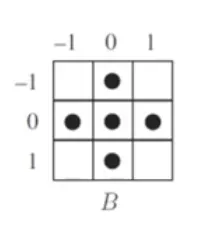
응용예 : 경계선 검출 (boundary detection)
•
A 와 B 는 이진 (binary) 영상 화소들의 집합이다.
•
A 는 영상이라고 하자.
•
B 는 원점에 대해 대칭적인 점들로 구성되는 커널이라고 하자.
•
internal boundary = A - erosion(A, B)
•
external boundary = dilation(A, B) - A
•
morphological gradient = internal boundary + external boundary
응용 연산들
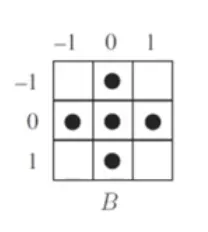
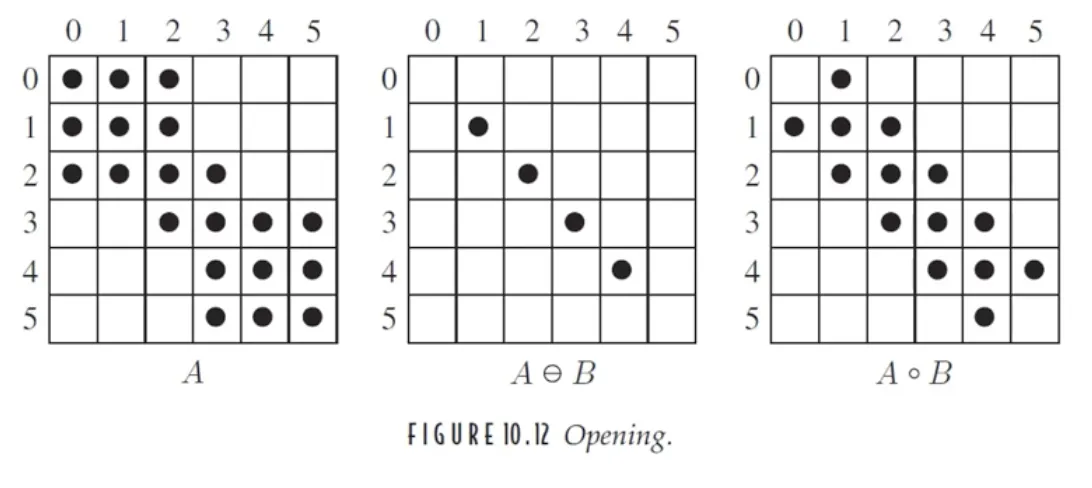
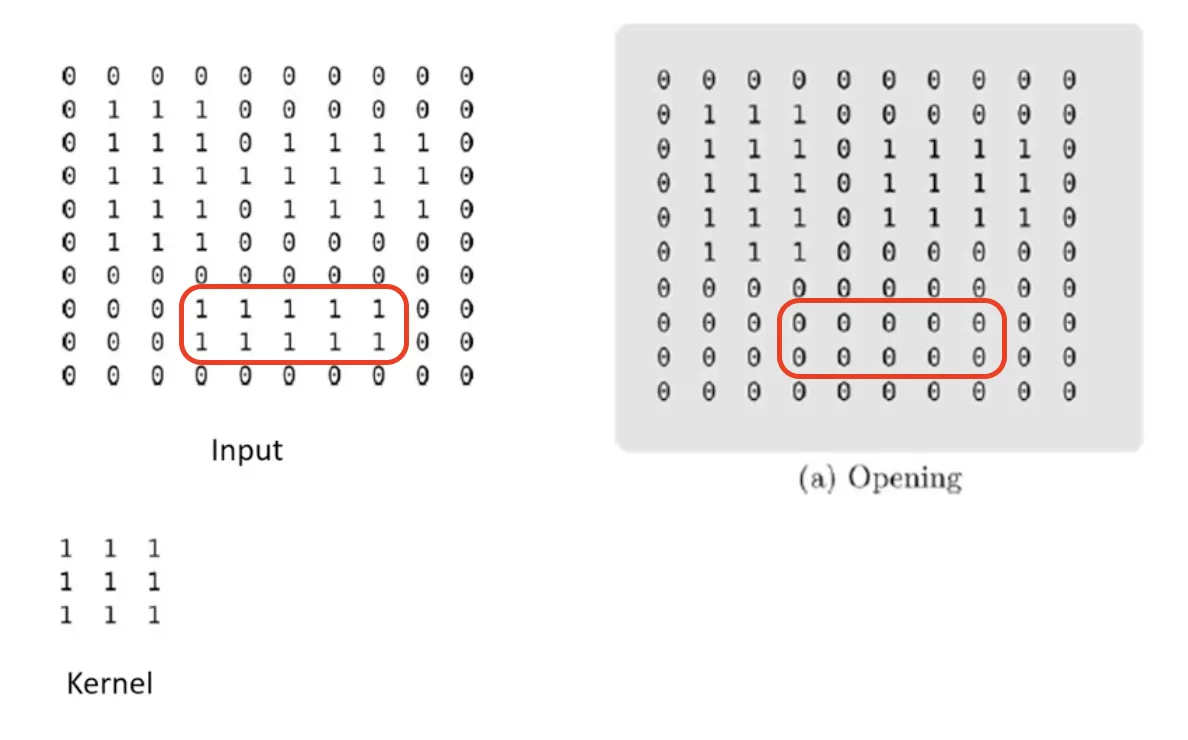
열림 연산 (opening)
침식 연산 후 팽창 연산을 하는 것을 열림 연산 (opening) 이라고 한다.
수학적 성질
•
열림 연산의 결과는 항상 원본 영상에 포함된다.
•
동일한 커널을 통한 열림 연산의 반복은 동일한 결과를 만든다.
•
영상 A 와 부분집합 관계를 가지는 영상 C 가 있다면, 동일한 커널을 적용한 결과 또한 부분집합 관계이다.
형태적 성질
•
좁은 연결점을 끊고, 돌출부분을 제거하는 경향이 있다.
•
영상을 smoothing 하는 경향이 있다.
왜 "좁은 연결점을 끊고, 돌출부분을 제거하는 경향이 있다." 같은 성질을 가지게 되는지 직관적으로 이해해 보자. 수축은 인코딩 - 팽창은 디코딩이라고 생각할 수 있다. 수축을 할 때, 살아남을 수 있는 픽셀로 선택받는 조건은 굉장히 팍팍하다. 영상과 커널이 and 연산을 거치기 때문이다. 여기서 살아남은 픽셀들만 원본으로 복원시킬 (팽창) 권한을 받게 된다는 말이다. 만약 수축된 영상이 모든 픽셀 정보를 다 담고 있게 되는 경우, 팽창의 결과와 원본의 결과물은 동일할 것이다. 이것을 이해하고 난 뒤, 열림연산의 수학적 성질을 본다면, '아 그럴 수밖에 없구나' 싶다.
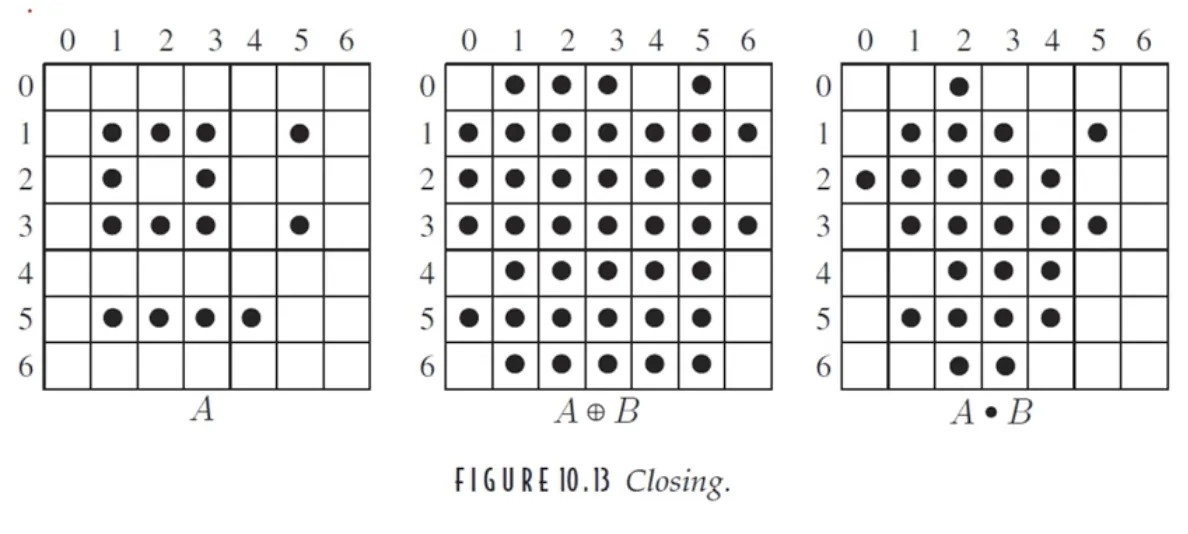
닫힘 연산 (closing)
침식 연산 후 팽창 연산을 하는 것을 열림 연산 (opening) 이라고 한다.
수학적 성질
•
원본 영상은 닫힘 연산의 결과에 항상 포함된다.
•
동일한 커널을 통한 닫힘 연산의 반복은 동일한 결과를 만든다.
•
영상 A 와 부분집합 관계를 가지는 영상 C 가 있다면, 동일한 커널을 적용한 결과 또한 부분집합 관계이다.
형태적 성질
•
갈라진 틈을 좁히며 작은 홀을 제거하는 경향이 있다.
•
영상을 smoothing 하는 경향이 있다.
왜 "갈라진 틈을 좁히며 작은 홀을 제거하는 경향이 있다." 같은 성질을 가지게 되는지 직관적으로 이해해 보자. 이 연산은 작은 기회놓치지 않는다. 그리고 그것을 다시 수축시킨
응용예 : 열림과 닫힘을 활용한 잡음 제거
열림 연산과 닫힘 연산을 한 번씩 적용하면, 소금&후추 (임펄스) 잡음 을 제거할 수 있다.
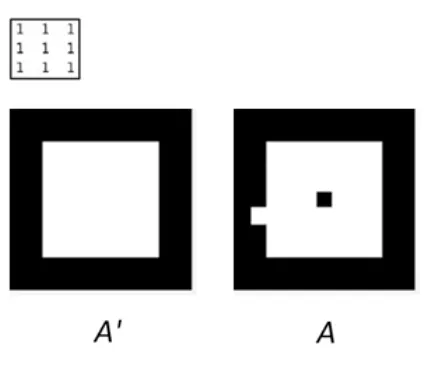
A 는 원본 영상 A' 에서 소금& 후추 잡음 (salt and pepper noise, impulse noise, 참고 :  영상의 열화와 복원) 가 발생한 영상의 예시이다. 어떻게 잡음을 제거할 수 있을까
영상의 열화와 복원) 가 발생한 영상의 예시이다. 어떻게 잡음을 제거할 수 있을까
침식 연산
침식 연산 결과에 팽창 연산을 한번, 두 번 한 결과
좌 : (침식 → 팽창)
우 : (침식 → 팽창) → 팽창
•
열림 연산은 0 의 위치의 1 의 잡음을 제거하는 데에 효과적일 수 있다.
(침식 → 팽창) → (팽창 → 침식)
•
닫힘 연산은 1 의 위치의 0 의 잡음을 제거하는 데에 효과적일 수 있다.
열림 연산과 닫힘 연산을 한 번씩 적용하면 잡음을 제거할 수 있겠다.
•
침식 연산을 적용한 뒤, 팽창 연산을 적용한 것은 열림 연산이니까 (opening)
•
팽창 연산을 적용한 뒤, 침식 연산을 적용한 것은 닫힘 연산이니까 (opening)
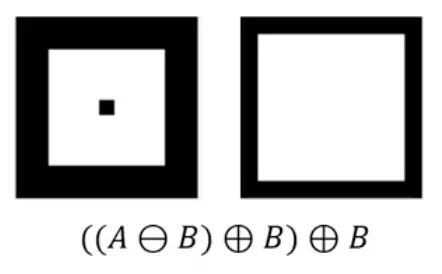
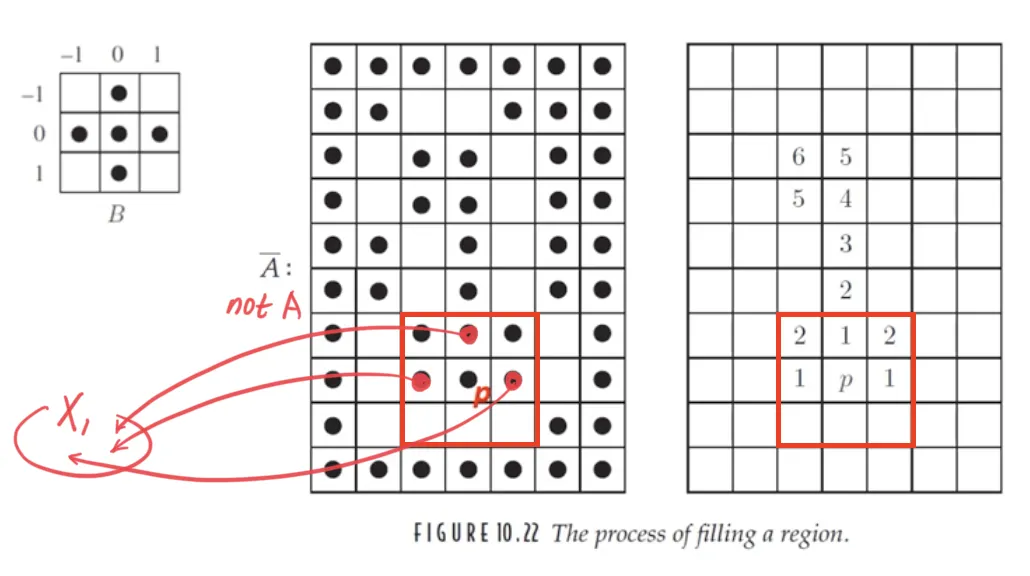
응용예 : 영역 채우기 알고리즘 (region filling)
p 와 B 의 팽창 연산 수행 결과와 ~A 의 교집합을 계산하는 동작을 반복하여 영역을 채울 수 있다.
좌 : B, 중앙 : not X, 우 : result
•
p 는 씨앗과 같은 존재로, 내부 영역의 하나의 픽셀은 알고 있다는 것을 전제로 알고리즘이 돌아간다.
•
변화가 없을 때까지 반복하며, 최종적으로 모든 집합 X 의 합집합을 결과물로 만든다.
def dilation(binary_im, kernel=None):
im = binary_im.astype(np.uint8)
if kernel is None:
kernel = np.array([
[0, 1, 0],
[1, 1, 1],
[0, 1, 0],
], dtype=np.uint8)
im = cv2.dilate(im, kernel, iterations=1)
im = im.astype(np.bool)
return im
def region_filling(im, initial_position):
binary_im = (im / 255).astype(np.bool)
not_im = ~binary_im
x_n = np.zeros_like(im).astype(np.bool)
x_n[initial_position] = 1
last_count = 0
while np.count_nonzero(x_n) != last_count:
last_count = np.count_nonzero(x_n)
x_n = dilation(x_n)
x_n = x_n & not_im
x_n = (x_n * 255).astype(np.uint8)
return x_n
row = 50
col = 200
im = region_filling(im_circbw, (row, col))
plt.figure()
plt.imshow(im, cmap='gray')
Python
복사
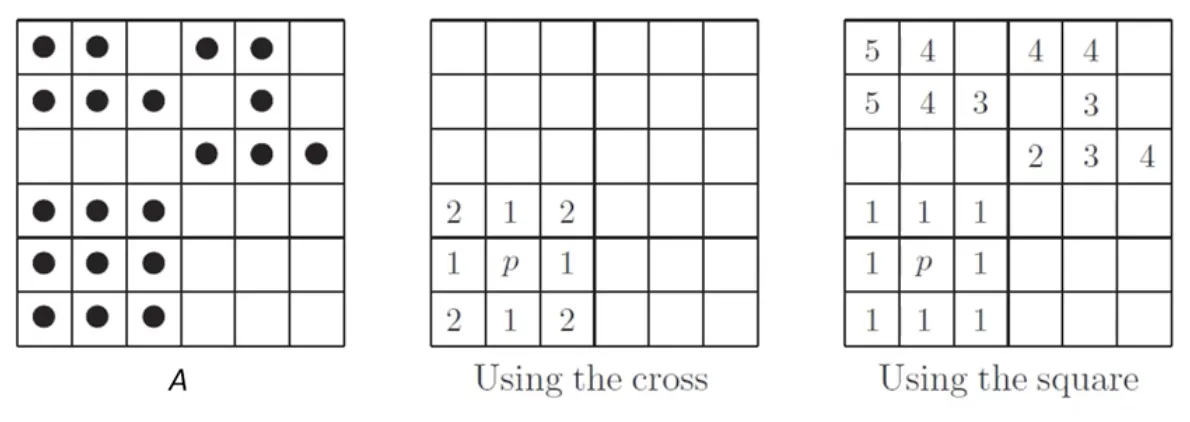
응용 : 연결성분 확인 알고리즘 (connected component)
연결성분 알고리즘은 어떻게 연결되어 있는지 파악하는 알고리즘이다.
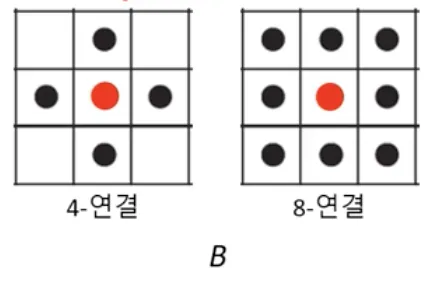
연결을 정의하는 일반적인 방법으로는 4연결과 8연결이 있다.
4연결 성분을 교차형 구조 커널이라고 한다.
8연결 성분을 정방형 구조 커널이라고 한다.
•
p 는 씨앗과 같은 존재로, 내부 영역의 하나의 픽셀은 알고 있다는 것을 전제로 알고리즘이 돌아간다.
•
p 점으로부터 어떤 요소가 연결되어 있는지 알아낼 수 있다.
•
변화가 없을 때까지 반복하며, 최종적으로 모든 집합 X 의 합집합을 결과물로 만든다.
def connected_component(im, initial_position, kernel=(3,3), kernel_type='8_connected'):
binary_im = (im / 255).astype(np.bool)
x_n = np.zeros_like(im).astype(np.bool)
x_n[initial_position] = 1
last_count = 0
while np.count_nonzero(x_n) != last_count:
last_count = np.count_nonzero(x_n)
if kernel_type == '4_connected':
raise NotImplementedError
elif kernel_type == '8_connected':
x_n = dilation(x_n, kernel=np.ones(kernel))
else:
raise NotImplementedError
x_n = x_n & binary_im
x_n = (x_n * 255).astype(np.uint8)
return x_n
row = 70
col = 50
im = connected_component(im_nicework, (row, col), kernel=(3,3))
plt.figure()
plt.imshow(im, cmap='gray')
Python
복사
kernel = (3,3)
kernel = (20,20)
•
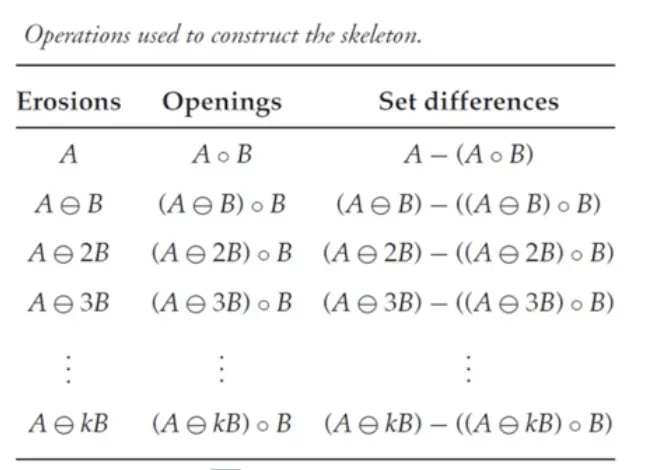
응용 : 골격화 처리 알고리즘 (skeletonization)
골격화 처리 (skeletonization) 이란 이진영상에서 물체의 골격을 찾는 알고리즘이다.
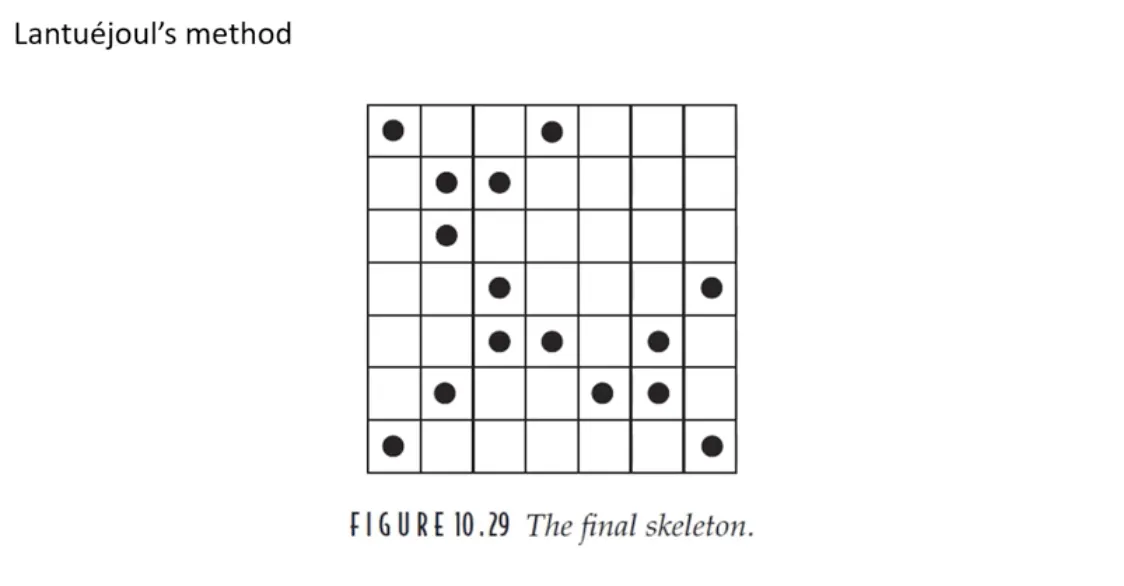
골격을 정의하는 방법은 다양하다. 이번 예제에서는 Lantuejoul's method 를 사용한다.
•
변화가 없을 때 (Opening 이 공집합이 될 때) 까지 반복하며, 최종적으로 모든 집합 X 의 합집합을 결과물로 만든다.
직관적으로 이해해 보자.
A 에 열린연산을 적용하면 열림연산 정리에 따라 A 의 부분집합만 남는다.
뭐, 예를 들어 A 의 B 에 대한 열림연산의 결과를 O 라고 하고 O 는 A 의 90% 가 남았다고 쳐 보자.
이때 O 는 당연히 A 의 중심부이고, 제거되는 부분인 (A-O) 는 변두리에 가깝다.
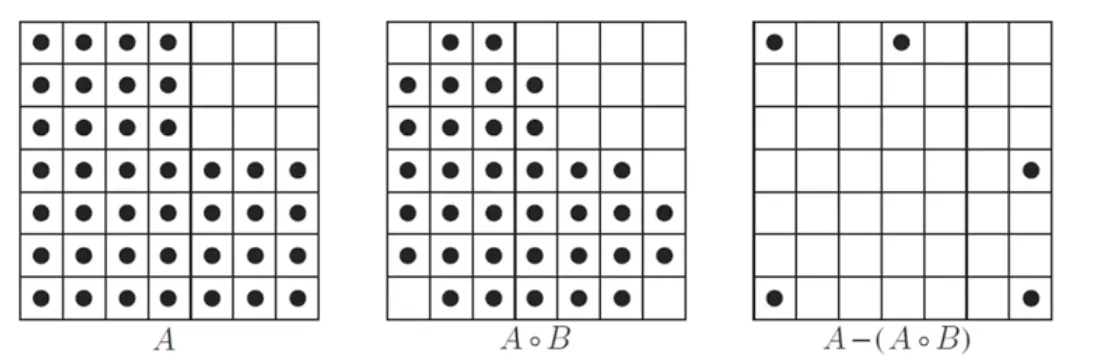
아래 그림으로 시각적인 예시를 확인해 보자.
원본 이미지를 여러 번 침식해 보며, 여러 번 침식된 영상에 변두리를 다시 구한다. A'=(A-kB)
침식된 이미지 A' 에서 열림연산을 취하고 그 나머지를 구해 (A'-O') 라는 변두리를 얻는다.
이렇게 얻은 찌꺼기 (변두리) 들을 전부 모으면, 골격처럼 보인다.
응용 : Grayscale 영상에서의 형태적 처리
지금까지는 binary image 에 대해서만 적용했다.
이것을 일반화해서 grayscale 영상에 적용할 수 있도록 만들어 보자.
침식 및 팽창 연산의 일반화
binary 영상에서 특정 커널에 의한 침식 연산은 아래와 동일한 연산이다.
1.
커널의 원소 값이 0 이고, 영상에 elementwise subtraction 을 적용
2.
min value pooling
binary 영상에서 특정 커널에 의한 팽창 연산은 아래와 동일한 연산이다.
1.
커널의 원소 값이 0 이고, 영상에 elementwise addition 을 적용
2.
max value pooling
식으로 풀어쓰면 아래와 같다.
1.
elementwise addition / subtraction
2.
min / max pooling
열림 연산과 닫힘 연산의 일반화
열림연산과 닫힘연산은 침식연산과 팽창연산의 일반화로 정의되므로 딱히 고민할 것이 없다.