영상의 위상기하학적 처리
영상의 아주 기본적인 형태에만 관심을 가질 때, 기본적 성질을 조사하는 것을
영상의 위상기하학 (image topology), 디지털 위상기하학 (digital topology) 라고 한다.
아 항상 사람들이 topology 분석 이런 이야기를 했던 것이,
그냥 기본적인 형태분석을 하겠다는 거였구나.
이와 관련된 task 의 예시를 한번 들어 보자.
•
흰색 blob 의 개수를 세어야 한다.
•
binary image 의 형태를 넘어 어떻게 흰 블록의 수를 셀 것인가?
이번 장에서는 우선 binary image 에 대해서만 다룬다.
용어 정리
terminology 를 잘 정의하고 가자.
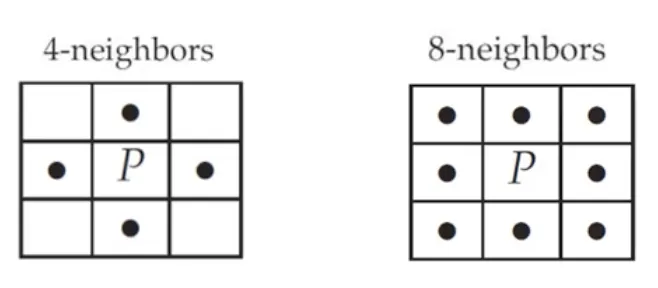
이웃화소 (Neighbors) 와 인접화소 (Adjacency)
인접 (adjacency) 이란 어떠한 조건 (conditions) 아래에서
어떤 픽셀이 어떤 픽셀 옆에 있다고 여겨지는 것이다.
인접 (adjacency) 한 화소를 이웃 (neighbor) 이라고 한다.
방금 배운 내용을 바탕으로, 위와 같은 상황을 정확히 서술해 보면
왼쪽 그림 : 상하좌우 네 방향만 인접하다고 할 것이다. 따라서 이웃은 네 개이다.
오른쪽 그림 : 상하좌우+대각선 모두를 인접하다고 할 것이다. 따라서 이웃은 여덟 개이다.
경로 (Path), 연결 (Connect), 성분 (Component)
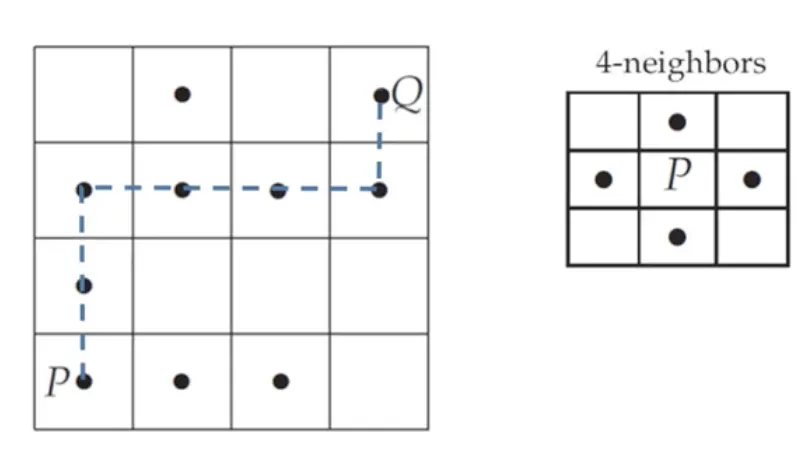
N-인접 화소를 이용해서 두 점 사이의 경로 (path) 를 구성할 수 있다.
두 점은 N-연결형태 라고 불린다.
N-연결할 수 있는 (N-연결된) 모든 화소들의 집합을 N-성분 (component) 이라고 한다.
방금 배운 내용을 바탕으로, 위와 같은 상황을 정확히 서술해 보면
4인접 화소로만 경로 (path) 를 구성한다면, 파란색 선과 같은 결과를 얻을 수 있고,
P 와 Q 는 왼쪽 그림에 존재하는 수많은 4-연결형태 중 하나라고 볼 수 있다.
또한 왼쪽 그림에 보이는 모든 점들은 전부 4-성분 (component) 이다.
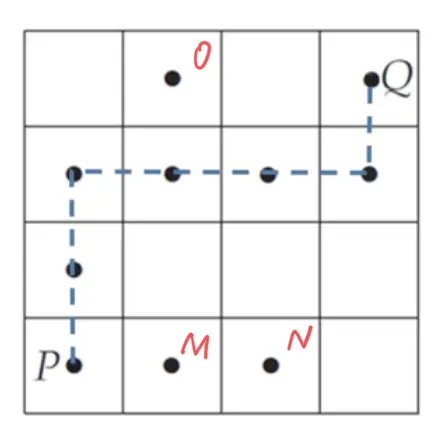
위 그림에서 P,Q 뿐 아니라 (M,N), (M,O), (N,O) 또한 모두 4-연결형태이다. 모든 4-연결형태를 이룰 수 있는 화소들의 집합을 N-성분 이라고 부른다는 점에 주의하자.
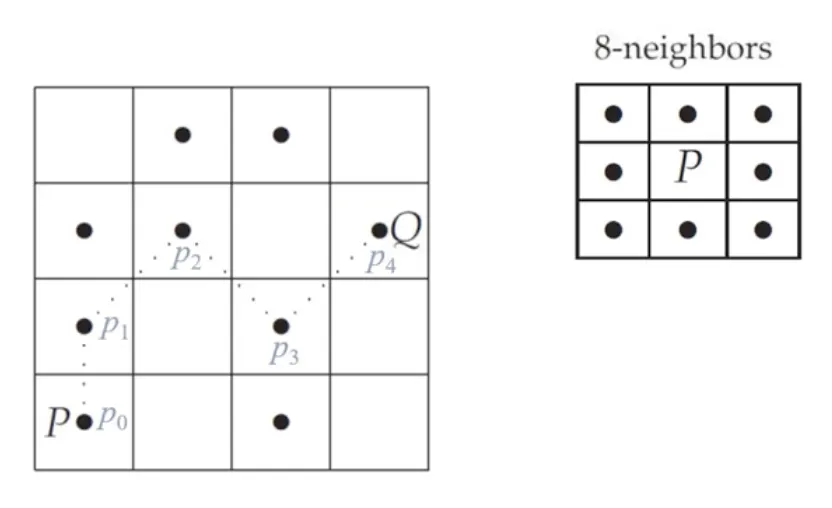
8인접 화소로만 경로 (path) 를 구성한다면, 파란색 점선과 같은 결과를 얻을 수 있고,
P 와 Q 는 왼쪽 그림에 존재하는 수많은 8-연결형태 중 하나라고 볼 수 있다.
또한 왼쪽 그림에 보이는 모든 점들은 전부 8-성분 (component) 이다.
그림에는 4-연결형태로부터 4-성분이 두 개, 8-연결형태로부터 8-성분이 한 개
존재한다는 사실을 볼 수 있다.
성분 (Component) 의 라벨링 (labeling)
라벨링 (labeling) 은 픽셀, 성분 등에 레이블을 붙이는 것을 의미한다.
이진 영상 (binary image) 에서 배경 (background) 이 아닌 것을 목적화소 (forground) 라고 한다.
1.
이진 영상 획득
2.
라벨링
3.
라벨의 수를 계산
Alg labeling:
위에서 아래로, 왼쪽에서 오른쪽으로 스캔하는 라벨링 알고리즘이다.
p 는 좌표
p_list 는 위->아래, 왼쪽->오른쪽 으로 정렬되어 저장되어 있는 이미지의 좌표 리스트
im 은 이진영상
label = 1
for p in p_list:
if is_forground(im, p):
for p' in kernel.interest_coord:
if is_labeled(im, p'):
write_two_pixel_is_same(im[p'].label, label)
label = im[p'].label
im[p].label = label
label += 1
Python
복사
kernel.interest_coord
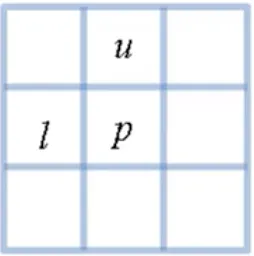
4-성분 라벨링
kernel.interest_coord=[u,l]
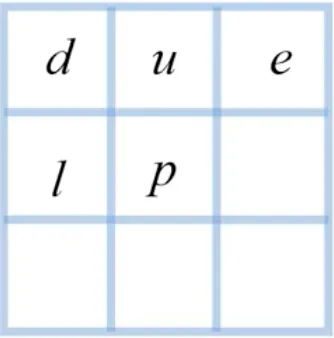
8-성분 라벨링
kernel.interest_coord=[d,u,e,l]
룩-업 테이블 (Look-Up Table, LUT)
Look up table 을 활용해서, binary image 에서 어떻게 N-경계를 찾을 수 있는지 알아보도록 하자.
•
영상처리의 시작: 샘플링, 카메라, 영상, 파일 구조, 색 공간 에서 index 이미지에 대해서 배웠다. 이때 RGB 이미지의 중복되는 색상을 하나의 정수로 표현해서, 이미지의 크기를 줄일 수 있다고 배웠다.•
화소 단위 영상처리 연산과 히스토그램 에서 grayscale 영상의 화소 단위 연산을 해야 하는 상황에서, 미리 lookup table 을 만들어두면 공간을 희생해서 엄청난 시간절약을 할 수 있다고 배웠다.
•
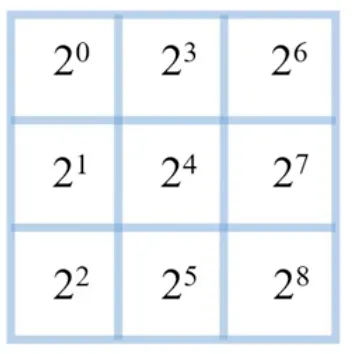
image 와 kernel 를 element-wise 로 곱하고 그 결과를 sum 한다. (spatial filter 과 비슷한 과정으로 동작한다고 생각하면 된다.) 이 연산으로부터 나온 결과 픽셀값 (pixel intensity) 가 index 이다.
•
결과 픽셀들 각각은 최소 0 ~ 최대 511 의 index 를 가질 수 있다. (총 512개)
•
각 위치가 하나의 bit 를 나타내기 때문에, 이 512 개의 index 각각이 나오는 경우는 상호배타적 (mutually exclusive) 이다.
•
이 경우들 중 어떤 경우에 경계영역인지 알아맞추기 등 연산을 하는 경우를 생각해 보자.
◦
예를 들어 4-경계를 검출하고 싶다면 어떻게 해야 할까?
1.
2^4 성분이 (4번째 비트) 1 이어야만 한다.
2.
2^3 성분 또는 2^1 성분 또는 2^5 성분 또는 2^7 성분 넷 중 하나라도 0 이 있어야 한다,
3.
(1, 2) 이들 경우에 해당할 수 있는 모든 index 들에, vector[index] = 1 을 만들어 둔다. 런타임에 복잡한 연산할 것 없이, elementwise multiply → sum 의 결과를 vector 내에서 찾으면 된다.
커널의 값을 위 그림처럼 함수값으로 표현한다고 했을 때 매트랩 인라인함수로 4-경계 판단 인라인함수를 만든 예시이다. 매트랩 인라인함수이지만 어렵지 않게 이해할 수 있다.