우리가 흔히 알고있듯, 이미지(영상) 을 표현하기 위해서는 (h, w, ch) 형태의 table 만 필요하다(참고4). 반면 3D 공간상의 대상은 이렇게 table 로 표현할 수 없다.
3D 공간을 표현하는 대표적인 포맷인 pointcloud 는 3D 공간의 대상에 대해 좌표 (x,y,z) 를 입력하면 색상값을 반환하는 함수 라고 볼 수 있다 (참고5). 이와 조금 다르게, NeRF 에서 함수 는 관측 위치 (x, y, z) 에 더해 density 와 direction 를 추가하여 수식으로는 와 같이 표현 가능하다. 이때 당연히 변환 함수 는 뉴럴넷이다(참고3).
여기서 direction 는 '유리' 나 '물방울' 과 같이 보는 방향에 따라 색상이 달라지는 3D 공간상의 피사체를 모델링하기 위해 추가되었다(참고2). 또다른 변수인 density 는 3D 공간상의 점이 밀(dense)한 정도 혹은 불투명한 정도를 표현한다. 직관적으로 매우 밀하지 않은(sparse) 기체의 경우 완전 투명하게 보이며, 고체의 경우 반대편이 보이지 않기 때문이다. 밀/소 외에도 유리창과 같은 피사체의 경우 그 너머가 보이지만 이보다 밀하지 않은 스펀지는 반대편이 보이지 않는다(참고1).
어떤 공간 위의 단 하나의 점만이 이미지평면에 맺히는 상의 색상에 기여한다고 여기는 투영 모델들에서는 거울 표면이나 유리, 색이 있는 액체같은 것들이 컴퓨터에 모델링되기 어려운 반면(참고6) pointcloud 와 달리 NeRF 를 사용하면 이런 요소들도 모델링할 수 있다.
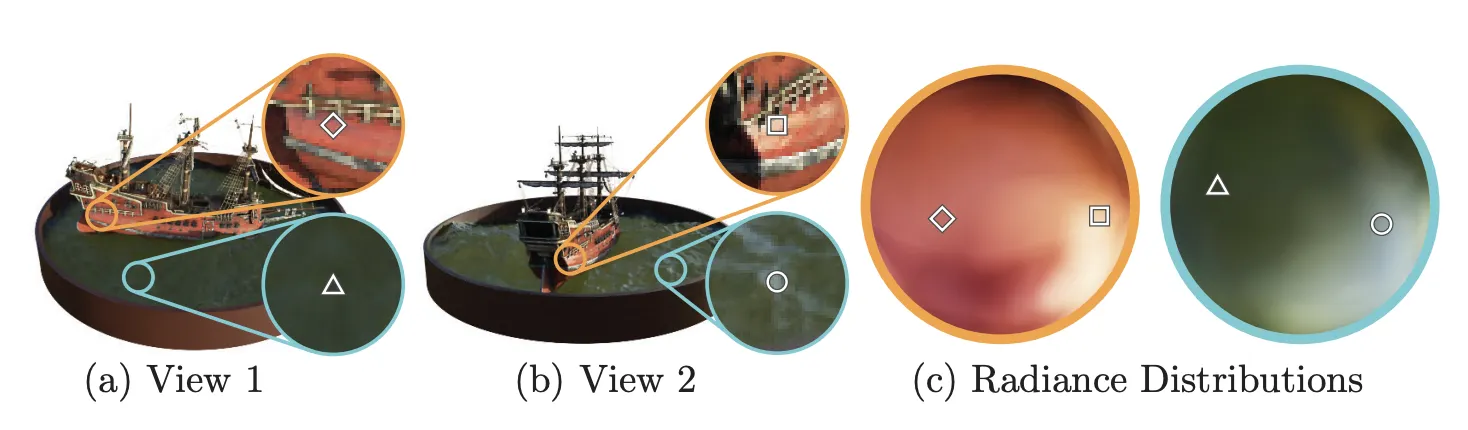
그림 (참고7), 실제로 동일한 3D 공간상의 점이라고 할지라도, 카메라가 바라보는 각도에 따라서 색상이 다르게 보일 수 있다!
그림 (c) 를 보자. NeRF 는 하나의 물리공간상의 지점에 대해, 보는 방향 d 에 따라 해당 지점이 어떤 모습으로 달라보일 수 있는지 연속적으로 모델링할 수 있다.
NeRF 구현하기
NeRF 의 특장점과 NeRF 가 기여하는 점
NeRF 의 한계와 이를 보완하는 것들이 있다.
NeRF 를 이용해 무언가 가치를 만들고 싶을 때, ‘점’ 표현이 아니라 ‘면’ 표현으로 바꿀 수 있어야 한다.
parse me
to
2.
참고