연립일차방정식이 형태로 만들어진다는 것은, 어떤 벡터 에 선형변환 을 취했을 때 영벡터가 된다는 것을 의미한다(from1). 딱 봐도 상당히 평범하지 않은 경우이다. 어떻게 선형변환을 하고 나서 운 좋게 영벡터로 똑 떨어진단 말인가.
선형 변환 행렬 가 변환 후 차원이 변환 전 차원을 보전하지 않을 때, 즉, 풀 랭크(
‣ Full Rank)가 아닌 경우에는(의문)(opp1: 차원이 쪼그라들지 않는 경우 Ax=0 문제), 영벡터를 제외하고도(참고3) 수많은 벡터들이 변환 후 영벡터가 될 수 있다(참고1). 따라서 풀 랭크가 아닌 선형 변환 행렬 가 포함된 식 의 해는 유일하지 않다. 따라서 이 조건에 부합하는 를 서술할 때에는 하나의 벡터로 서술할 수 없기 때문에, 해가 존재하는 공간(‣ Null space (Kernel))을 표현해야 하는 문제가 된다.
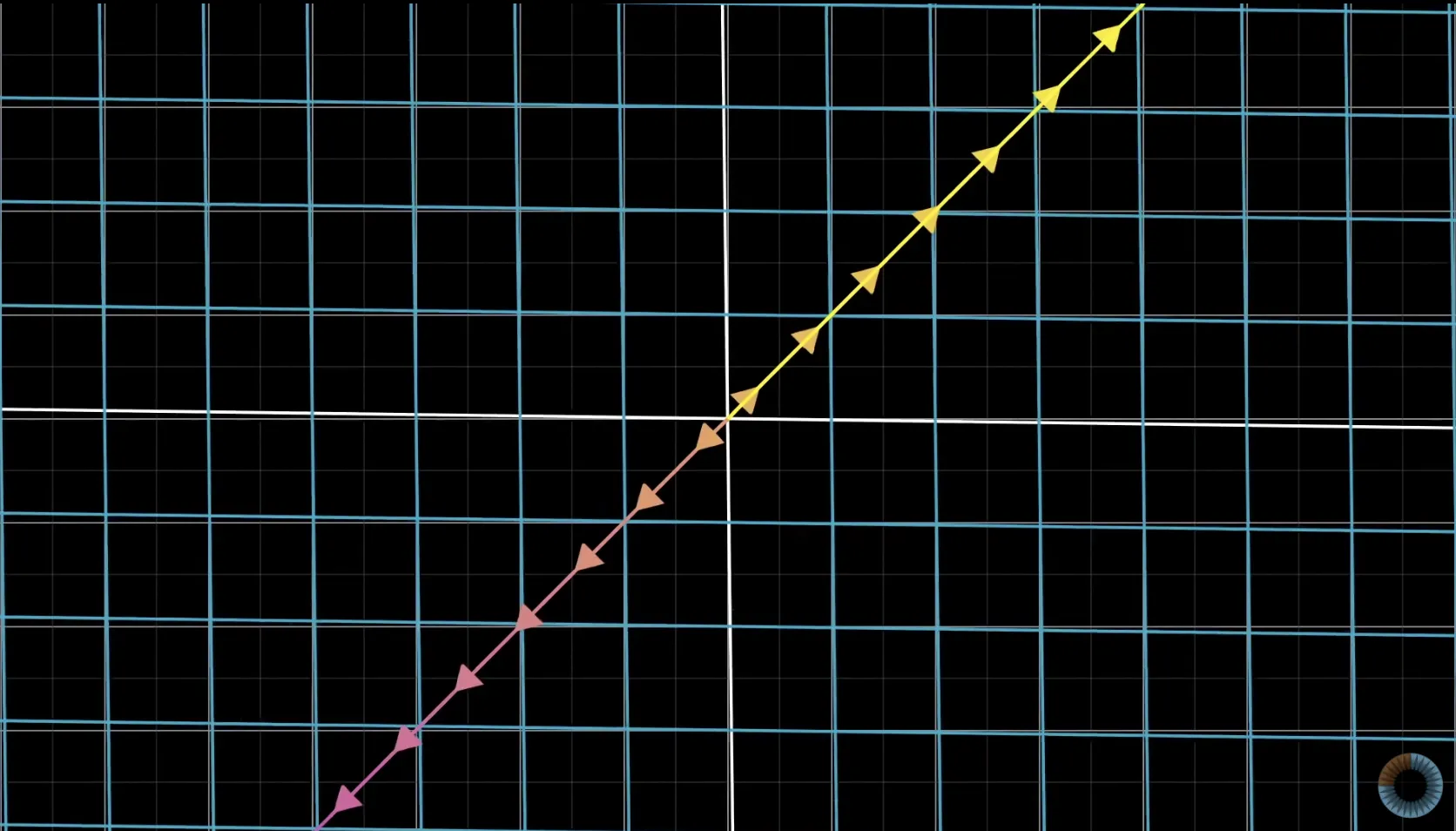
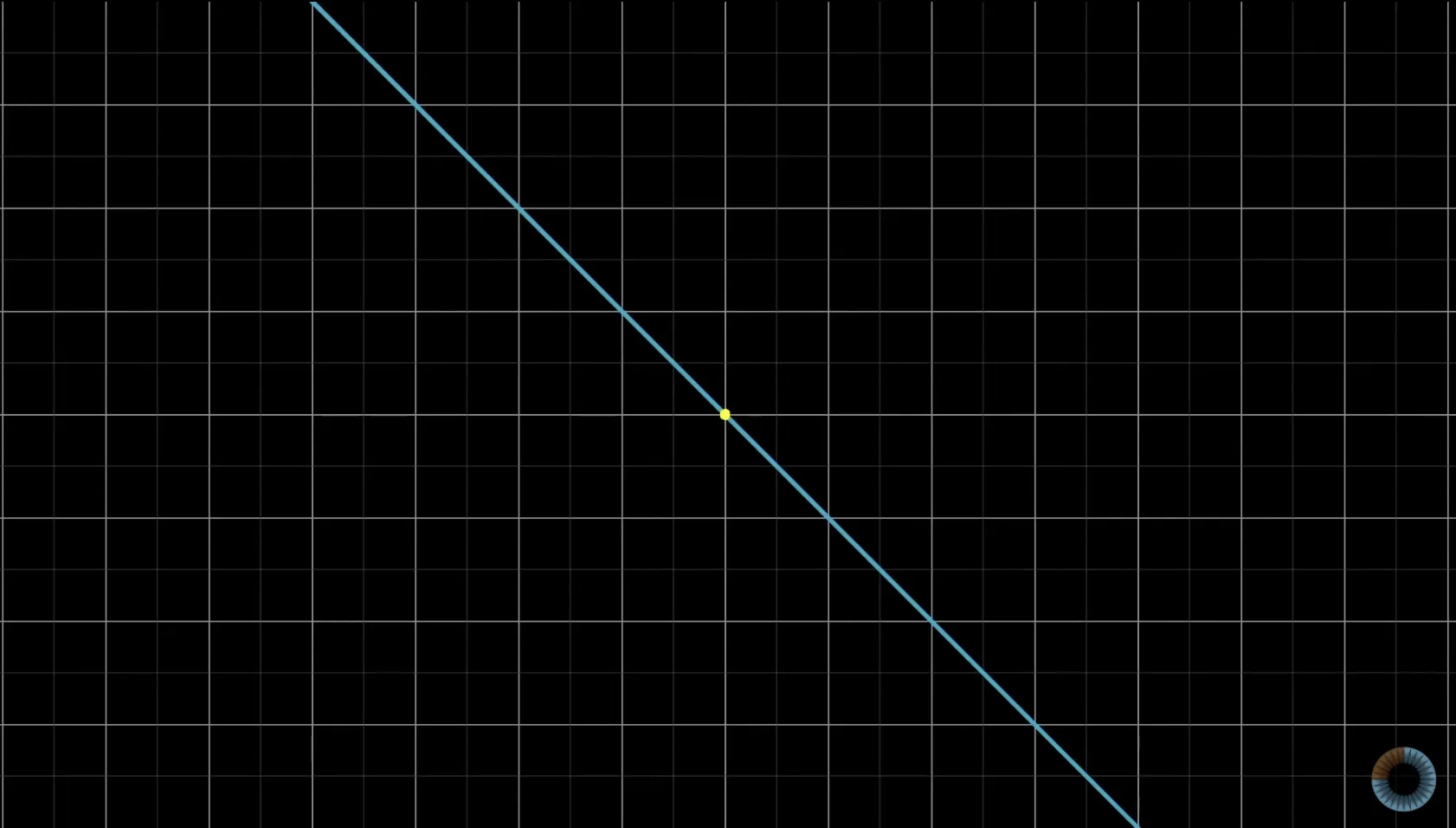
‣ Full Rank)가 아닌 경우에는(의문)(opp1: 차원이 쪼그라들지 않는 경우 Ax=0 문제), 영벡터를 제외하고도(참고3) 수많은 벡터들이 변환 후 영벡터가 될 수 있다(참고1). 따라서 풀 랭크가 아닌 선형 변환 행렬 가 포함된 식 의 해는 유일하지 않다. 따라서 이 조건에 부합하는 를 서술할 때에는 하나의 벡터로 서술할 수 없기 때문에, 해가 존재하는 공간(‣ Null space (Kernel))을 표현해야 하는 문제가 된다.그림 (참고1)
(1) 변환 전 좌표계(하늘색 격자)에 존재하는 벡터들 중 일부 집합(그라데이션)
(2) 2차원 좌표계가 1차원(푸른 선) 으로 변환됐고, (1)에 나타나 있는 모든 벡터들이 영벡터가 되었다.
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료들.
from : 과거의 어떤 생각이 이 생각을 만들었는가?
1.
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는가?
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는가?
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되고 이어지는가?
1.
참고 : 레퍼런스