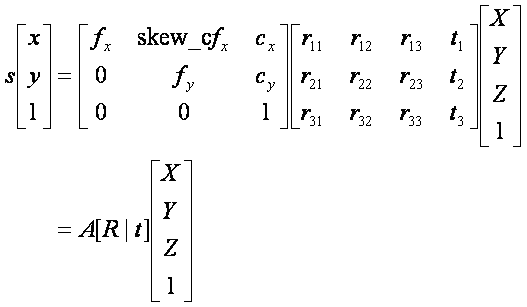🌍

deer.a2_2. title: 동차좌표계와 핀홀 카메라 모델의 행렬 표현

🚀 prev note

♻️ prev note

🚀 next note

♻️ next note

17 more properties

(kx, ky,k)=(x,y,1)=(x,y)

0이 아닌

k

가 곱해진 모든

(kx, ky, k)

에 대해서

(x,y)

또는

(x,y,1)

과 동일한 점(point)이라고 보는 것이 동차좌표계(homogeneous coordinate)이다.

당연히 여기에서 등호가 있다고 연산할 때 마음대로 치환해도 된다는 것은 아니다.

(kx, ky, k)

는 동차좌표계에서 정의된 점이고,

(x, y)

는 유클리드 좌표계에서 정의된 점이기 때문이다.

W=(X,Y,Z)

(x',y',z')=(x,y)=(x'/z',y'/z',1)

(2d 에서는 모든 z' 에 대해 공평해!)

이렇게 표현하는 이유는, 모든 z' 에 대해 (참고3), 또는 카메라 원점 좌표계 기준 3D 공간상의 점의 모든 Z 방향 값 (참고1 의 notation) 에 대해서 상관없는 점임을 표현할 수 있기 때문이다.

이를 생각해 두고, 핀홀 카메라 모델의 투영식 (참고2) 을 이해해 볼 수 있다.

그림 (참고2)

s(x,y,1) = KA[R|t](X,Y,Z,1)

계수 s (참고1:k의 역할과 비슷함) 를 밖으로 빼준다고 생각해 보자. 남은 벡터 [x, y, 1] 은 x'/z' 와 y'/z' 를 표현한 것일 뿐이다.

동적좌표계를 사용했을 때 저절로 따라오는 장점은 2D 를 3D 상에서 올리면서 복잡해질 것 같음에도 오히려 기하적 특징들을 해석하기가 더 쉬워진다는 점이다 (참고1). 가령 정규이미지 평면은 카메라 좌표계와 거리가 1 만큼 (단위거리만큼) 떨어진 평면이다. 2D 카메라 원점 좌표계를 동차 좌표계로 표현하면 아주 쉽게 실제 '거리가 1 만큼 떨어진 점' 이라는 의미를 띠도록 만들 수 있다.

참고

14p, Represent a 2D point (x,y) (참고1) by a 3D point (x’,y’,z’) by adding a “fictitious” third coordinate. Note: (x,y) = (x,y,1) = (2x, 2y, 2) = (kx, ky, k) for any nonzero k (can be negative as well as positive)

카메라 영상은 3차원 공간상의 점들을 2차원 이미지 평면에 투사(perspective projection)함으로써 얻어집니다. 핀홀(pinhole) 카메라 모델에서 이러한 변환 관계는 다음과 같이 모델링됩니다. (그림 참고)  s[x,y,1] = KA[R|t](X,Y,Z,1) 여기서, (X,Y,Z)는 월드 좌표계(world coordinate system) 상의 3D 점의 좌표, [R|t]는 월드 좌표계를 카메라 좌표계로 변환시키기 위한 회전/이동변환 행렬이며 A는 intrinsic camera matrix입니다. 

시점으로 보이는 점들의 위치가 중요한 것이 아니라 시점으로 부터의 방향이 중요하기 때문에 동차좌표를 사용합니다. 서로 다른 3차원의 점도 2차원에 투영 될 때는 하나가 되버린다는 점을 알 수 있습니다. (참고 : 달리 말하면, 하나의 2차원의 점도 서로 다른 3차원의 점이 될 수 있다.)

3:14, 그래서, 사실은 우리는 다른 언어를 사용하고 있다. 3:40, 공간 자체는 본질적으로 그리드를 가지고 있지 않는다. 다른 좌표계에 서식하는 Jennifer 이 그리드를 그린다고 해도, 이것은 단순히 만들어진 구조물일 뿐이다. 그녀의 좌표를 이해하는 데 도움이 되면 그만이다. 제니퍼의 공간에서 표현되는 벡터를 우리 방식대로 표현하고 싶다면, 제니퍼 공간의 기저를 알면 된다. 6:35 이 행렬이 하는 일은, 우리의 오해를 제니퍼가 의미하는 바로 변환시키는 것이다. 기하적으로, 이 행렬은 우리의 그리드를 제니퍼의 그리드로 변환시키는 것이다. 수치적으로, 이 행렬은 그녀의 언어에서 우리의 언어로 변역하는 것이다. … 10:25 제니퍼의 언어로 쓰여진 임의의 벡터로 시작한다. 그녀의 언어에서 무엇이 일어나는지 따라가기보다는 먼저 기저행렬의 변환을 통해 우리의 언어로 번역할 것이다. (공간적으로는 그녀 좌표공간으로 옮겨가는거지만 수치적으로는 그녀의 언어를 우리 언어로 번역하는 것이다. 열벡터 각 요소는 그녀의 기저벡터가 우리 언어의 무엇을 의미하나는지 나타낸다.) 그리고 우리의 언어에서 벡터를 움직인다. 마지막으로 역행렬을 곱해서 제니퍼의 언어로 되돌려놓는다. ... 11:43 이 과정으로 나오는 변환행렬은, 그녀의 좌표계에 있는 벡터에 곱할 때, 그녀의 언어로, 그녀의 좌표계에서 재표현되는 벡터가 나온다는 것이다. 그래서 같은 변환을 나타내고 싶지만 좌표계가 다를 때 A^(-1)MA 같은 표현이 사용되게 된다.