Search
🌍

deer.a2_2.1.1_1. title: 카메라 좌표계를 정의하는 방법은 다양하다. 좌표계를 어떻게 정의하냐에 따라 카메라 내부 파라미터(‣)의 부호가 달라진다.

🚀 prev note
♻️ prev note
🚀 next note
♻️ next note
18 more properties
‘좌표계의 기준이 [아래쪽, 오른쪽, 뒷쪽] 이다 혹은 [−y,x,z][-y, x, z] 이다.’ 라는 말은 무슨 말일까? 그렇다면 ‘COLMAP(참고2)에서 제시하는 좌표계(frame)는 [x,−y,−z][x, -y, -z] 이다' 같은 말은 도대체 무슨 뜻일까(참고1)? 둘이 다른 말이라면, 둘은 무슨 차이가 있을까?

Case 1

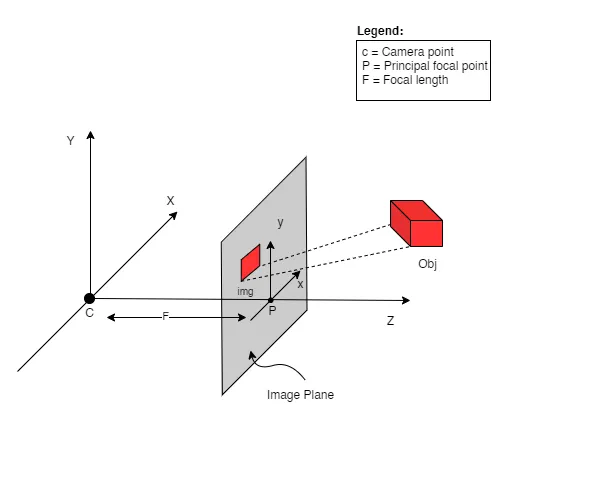
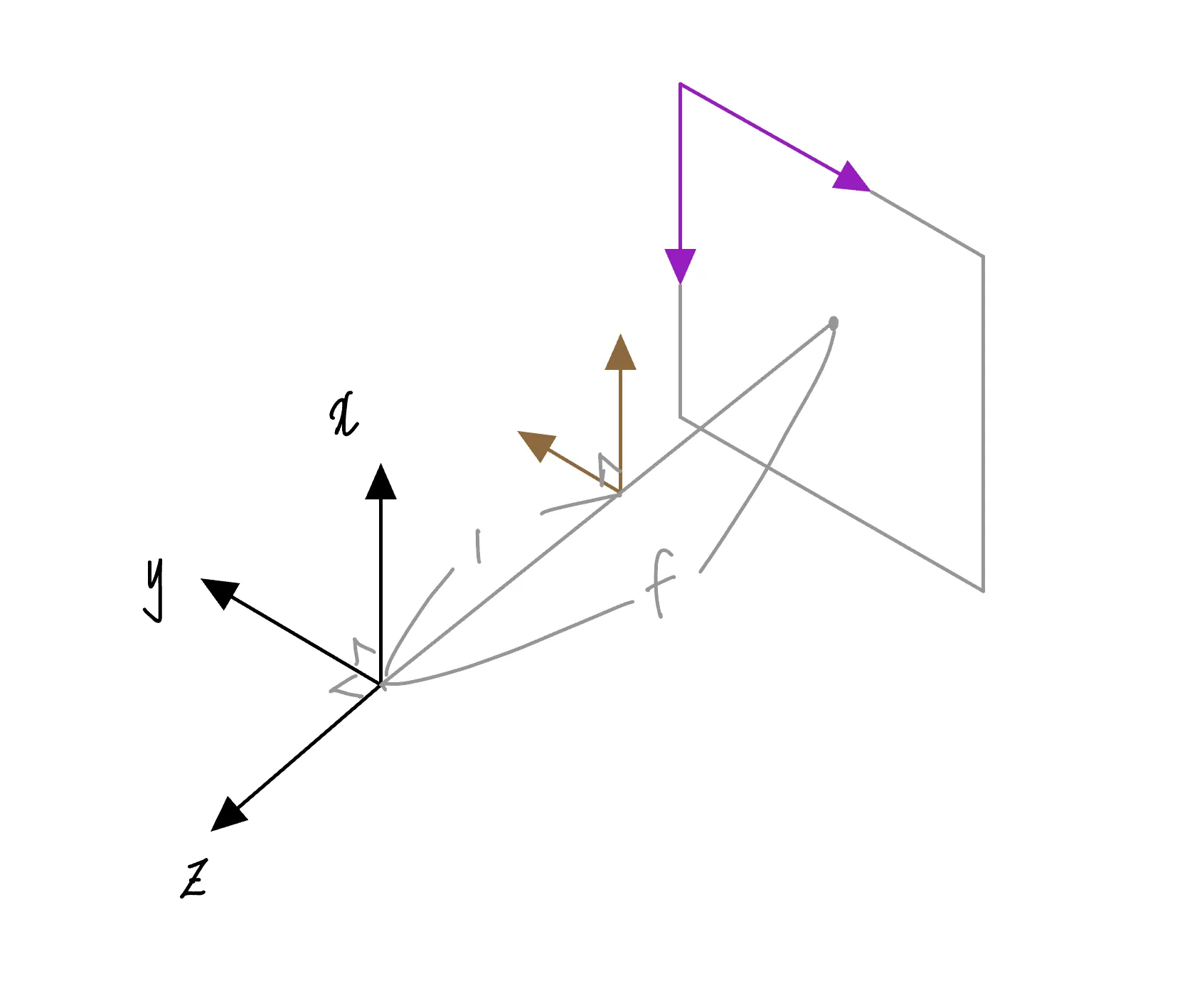
그림 (참고1)
위 그림을 보자. 위 그림에는 카메라 원점 좌표계와 이미지 평면 그려져 있고, 카메라 정규 좌표계는 생략되어 있다. 이 그림에 따르면, 카메라가 바라보는 방향이 +z+z 이다. 그러니까 ‘전방’ 이다. 오른손으로 위 그림의 좌표계를 표현해 보았다. 검지손가락을 나에게서 멀어지는 방향으로 두고 +z+z 방향이라고 둔다면, +x+x 은 왼쪽 방향, +y+y 는 윗쪽 방향이라고 할 수 있겠다.
카메라 원점 좌표
카메라 원점 좌표 (빨강), 이미지 좌표 (연녹). 기저벡터의 길이 차이를 표현했다.
3D 공간상에 존재하는 점인데, 카메라 원점 좌표계의 언어로 해석한 좌표값 {}x(ox,oy,oz)\mathrm{x_{(o_x,o_y,o_z)}}를(혹은 정규 이미지 좌표계의 언어로 해석한 좌표값 x(u,v)\mathrm{x_{(u,v)}}를(from4)), 이미지 평면 좌표계 의 언어 x(p,q)\mathrm{x_{(p,q)}}로 해석하고 싶다고 생각해 보자(from3). 둘 사이의 관계를 정의하는 변환 K\mathrm{K} 는 다음과 같이 표현 가능하다. 이때 좌표들이 동차좌표라는 뜻을 담기 위해 HG\mathrm{HG} 를 적어 주었다(from2).
(1):x(p,q)HG=Kx(ox,oy,oz)(1):\mathrm{x_{(p,q)}^{HG}=Kx_{(o_x,o_y,o_z)}}
(2):x(p,q)HG=Kx(u,v)HG(2):\mathrm{x_{(p,q)}^{HG}=Kx_{(u,v)}^{HG}}
카메라 내부 파라미터의 정의에 따라, f>0f>0 이다. 또한, 위 그림으로 보았을 때 kx,ky<0k_x, k_y<0 (from5)이고, cx,cy<0c_x, c_y<0 이다. 동차좌표의 정의에 따라, x(p,q)=(p,q)=(hp,hq,h)HG=x(p,q)HG\mathrm{x_{(p,q)}}=(p,q)=(hp,hq,h)^{\mathrm{HG}}=\mathrm{x_{(p,q)}^{HG}} 이므로, (1)(1) 이든 (2)(2) 이든 여부에 상관없이 K\mathrm{K} 는 다음과 같이 모델링 가능하다. hh 의 부호는 당연히 모른다.
h∗(kxf)h * (k_xf)
0
h∗cxh*c_x
0
h∗(kyf)h * (k_yf)
h∗cyh*c_y
0
0
hh
부호를 관찰해 보자. hh 가 양수이면, 다음과 같은 결과가 나온다.
-
-
-
-
+
hh 가 음수이면, 다음과 같은 결과가 나온다.
+
+
+
+
-
뭐 어쩌라고..? 조금만 더 가보자.

Case 2

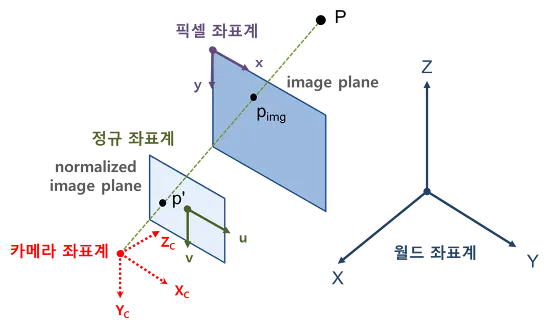
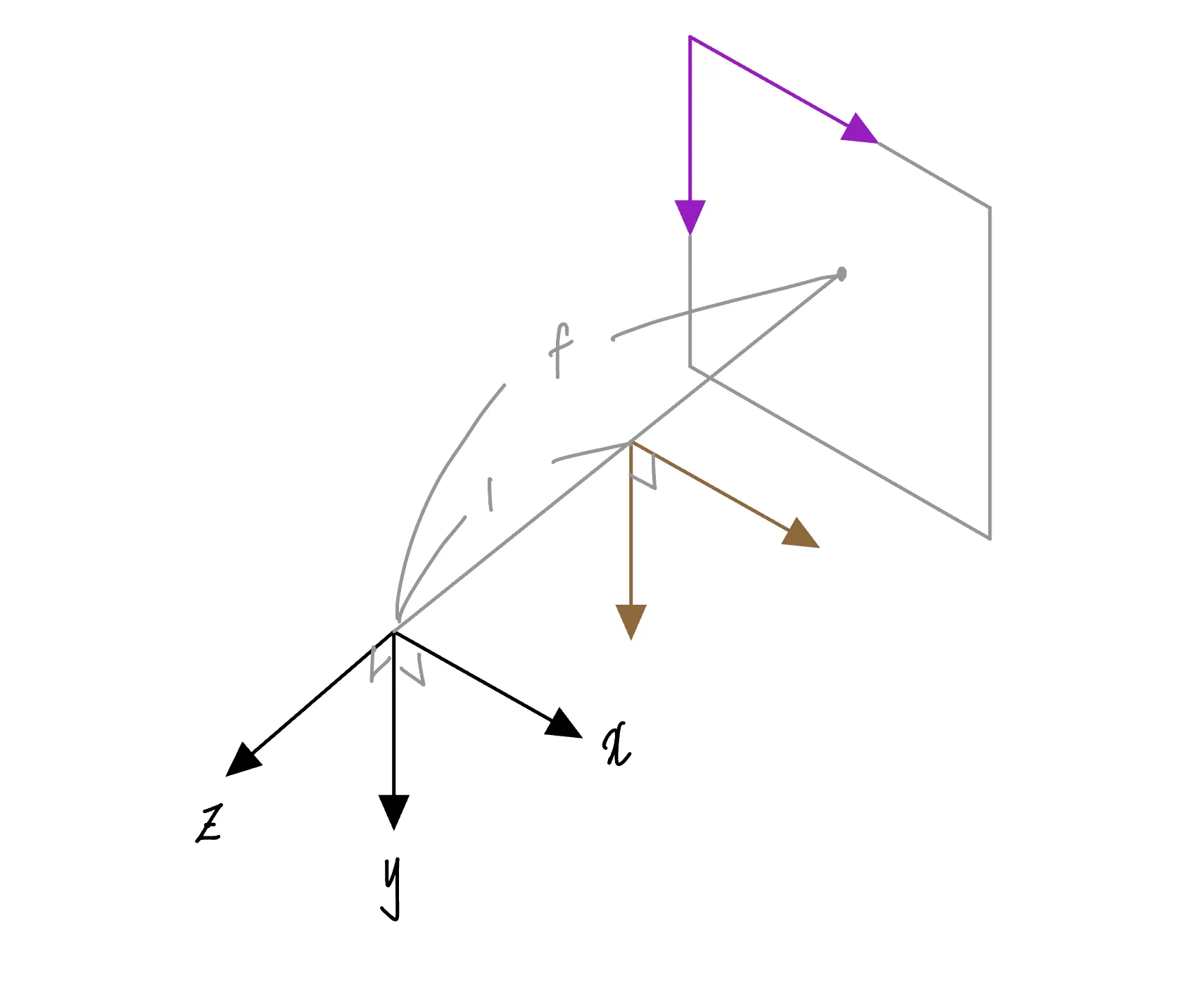
그림 (참고2)
이번에는 조금 다르게 생긴 그림을 가져왔다. 그림을 보자. 위 그림에는 카메라 원점 좌표계, 이미지 좌표계가 그려져 있고, 카메라 정규 좌표계도 그려져 있다. 이 그림에 따르면, 카메라가 바라보는 방향이 +zc+z_c 이다. 그러니까 ‘전방’ 이다. 이번에는 왼손으로 위 그림의 좌표계를 표현해 보았다. 검지손가락을 나에게서 멀어지는 방향으로 두고 +z+z 방향이라고 둔다면, +x+x 은 오른쪽 방향, +y+y 는 아랫쪽 방향이라고 할 수 있겠다.
카메라 원점 좌표
이 경우에도 카메라 내부 파라미터의 정의에 따라, f>0f>0 이다. 하지만, 이번 상황에선 이미지 좌표계의 좌표축 방향과 카메라 원점 좌표계의 방향이 동일하므로, kx,ky>0k_x, k_y>0 이고, 이미지 좌표계의 원점이 카메라 원점 좌표계 기준 음수 방향으로 평행이동했으므로 cx,cy>0c_x, c_y>0 이다. 이후는 똑같은 논리로, 동차좌표의 정의에 따라, x(p,q)=(p,q)=(hp,hq,h)HG=x(p,q)HG\mathrm{x_{(p,q)}}=(p,q)=(hp,hq,h)^{\mathrm{HG}}=\mathrm{x_{(p,q)}^{HG}} 이므로, (1)(1) 이든 (2)(2) 이든 여부에 상관없이 K\mathrm{K} 는 다음과 같이 모델링 가능하다. hh 의 부호는 당연히 모른다.
h∗(kxf)h * (k_xf)
0
h∗cxh*c_x
0
h∗(kyf)h * (k_yf)
h∗cyh*c_y
0
0
hh
부호를 보자. hh 가 양수이면, 다음과 같은 결과가 나온다.
+
+
+
+
+
hh 가 음수이면, 다음과 같은 결과가 나온다.
-
-
-
-
-

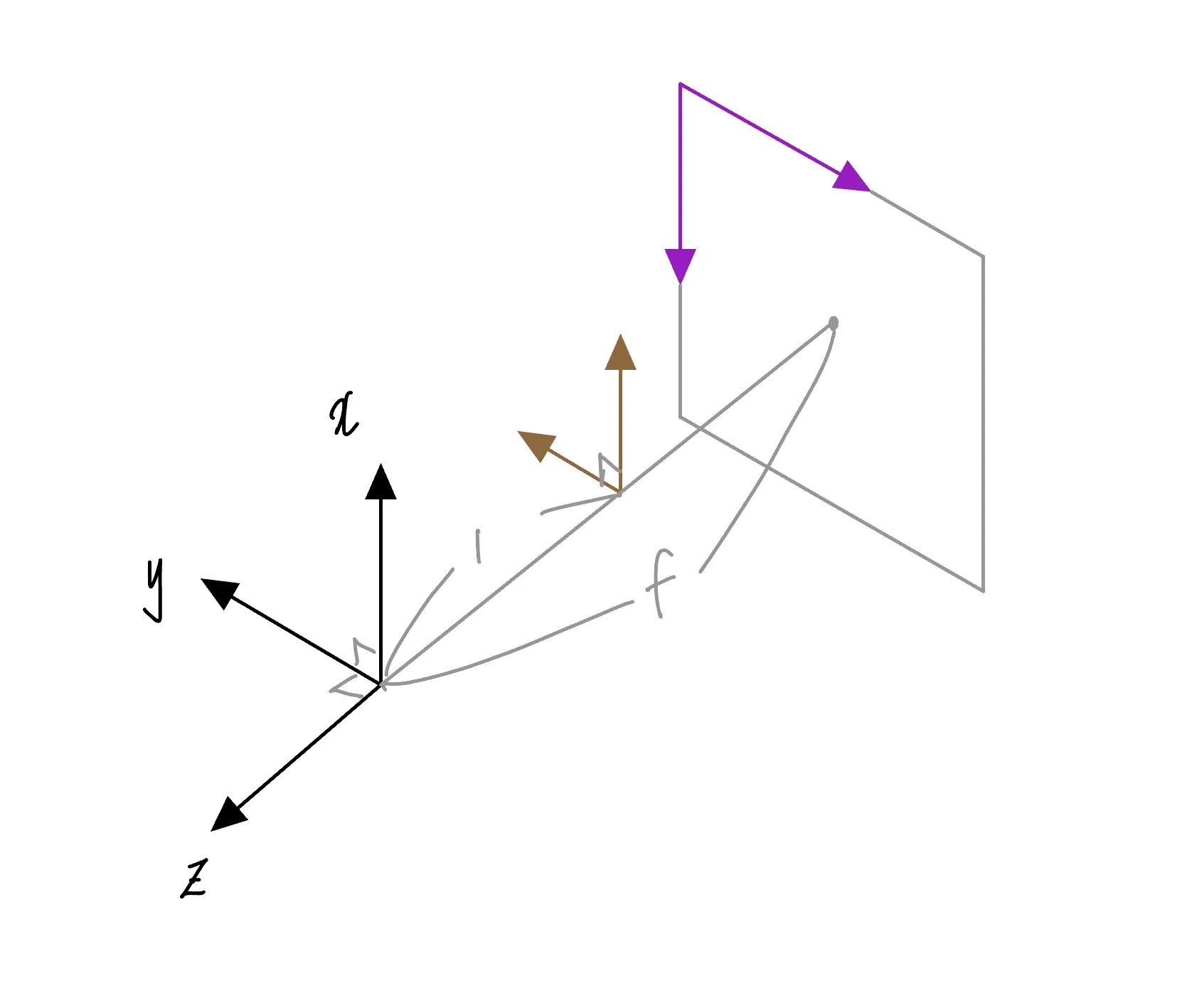
Case 3

위 그림에는 카메라 원점 좌표계, 카메라 정규 좌표계, 이미지 좌표계가 그려져 있다. 이 그림에 따르면, 지금까지 보았던 경우들과 반대로 카메라가 바라보는 방향이 −z-z 이다. 그러니까 ‘후방’ 이다.
카메라 내부 파라미터의 정의에 따라, f>0f>0 이다. 이번 상황에선 이미지 좌표계의 좌표축 방향과 카메라 원점 좌표계의 좌표축 방향이 반대이므로, kx,ky<0k_x, k_y<0 이고, 이미지 좌표계의 원점이 카메라 원점 좌표계 기준 양수 방향으로 평행이동했으므로 cx,cy<0c_x, c_y<0 이다.
hh 가 양수이면, 다음과 같은 결과가 나온다.
-
-
-
-
+
hh 가 음수이면, 다음과 같은 결과가 나온다.
+
+
+
+
-

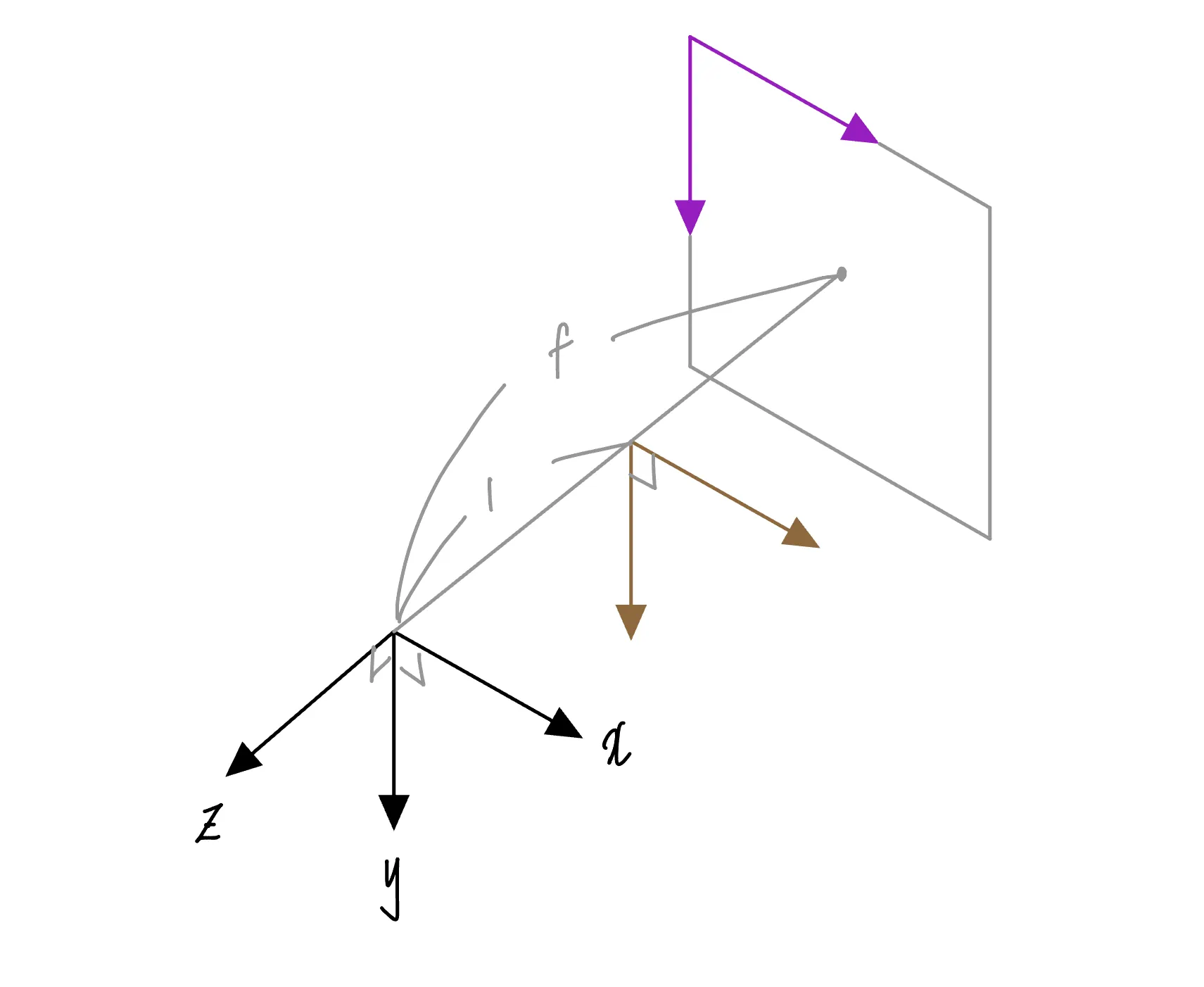
Case 4

위 그림에는 카메라 원점 좌표계, 카메라 정규 좌표계, 이미지 좌표계가 그려져 있다. 마찬가지로, 카메라가 바라보는 방향이 −z-z 이다. 그러니까 ‘후방’ 이다.
카메라 내부 파라미터의 정의에 따라, f>0f>0 이다. 이번 상황에선 이미지 좌표계의 좌표축 방향과 카메라 원점 좌표계의 좌표축 방향이 일치하므로, kx,ky>0k_x, k_y>0 이고, 이미지 좌표계의 원점이 카메라 원점 좌표계 기준 양수 방향으로 평행이동했으므로 cx,cy>0c_x, c_y>0 이다.
hh 가 양수이면, 다음과 같은 결과가 나온다.
+
+
+
+
+
hh 가 음수이면, 다음과 같은 결과가 나온다.
-
-
-
-
-
분명히 각각의 경우 카메라 내부행렬 K 의 구성원소들의 크기가 똑같더라도 부호는 다를수밖에 없다. 그런데 좌표계에 대한 명칭이나 기호, 좌표축 방향 등은 프레임워크에 따라, 사람에 따라 정의하기 나름이기 때문에 이에 따라서 조금씩 차이가 있을 수 있다(참고3). 카메라와 관련된 좌표계들의 방향이 서로 어떻게 관계하는지에 따라 카메라 내부 행렬 K 의 값이 내포하는 바가 달라지므로 이 부분을 인지하고 있어야 한다.
이제 마지막 사고 과정이다. 지금까지 사고과정의 핵심이 되었던 이 두 식에는 어떤 차이가 있을까?
(1):x(p,q)HG=Kx(ox,oy,oz)(1):\mathrm{x_{(p,q)}^{HG}=Kx_{(o_x,o_y,o_z)}}
(2):x(p,q)HG=Kx(u,v)HG(2):\mathrm{x_{(p,q)}^{HG}=Kx_{(u,v)}^{HG}}
두 식 중 특히 (1)(1) 에 주목해 보자. 식 (1)(1) 은 다음 식으로부터 쉽게 얻을 수 있다. 아래 식에서 x(wx,wy,wz)HG\mathrm{x^{HG}_{(w_x,w_y,w_z)}} 은 “3D 월드 좌표계의 언어로 해석한 3D 월드 위의 점의 동차좌표 표현” 을 나타낸다.
x(p,q)HG=K([R∣t]x(wx,wy,wz)HG)=Kx(ox,oy,oz)\mathrm{x_{(p,q)}^{HG}=K([R|t]x^{HG}_{(w_x,w_y,w_z)})=Kx_{(o_x,o_y,o_z)}}
x(ox,oy,oz)\mathrm{x_{(o_x,o_y,o_z)}}은 3차원 데카르트 좌표(Cartesian Coordinates in Euclidean World (Conventional Coordinates))이다. “3D 월드상에 존재하는 어떤 지점의 좌표를 카메라 원점 좌표계의 언어로 해석한 표현”이다. 즉, 카메라의 렌즈가 바라보고 있는 방향이 +z+z 라면, oz>0\mathrm{o_z}>0 이어야만 한다는 것이다. 하지만 렌즈가 바라보고 있는 방향이 −z-z 라면 oz<0\mathrm{o_z}<0 이어야만 한다. 즉, h>0, if oz>0h>0,\ if\ \mathrm{o_z}>0 이고 h<0, if oz<0h<0,\ if\ \mathrm{o_z}<0 이다. 정리하면 다음과 같다.

Case 1 의 K

-
-
-
-
+

Case 2 의 K

+
+
+
+
+

Case 3 의 K

+
+
+
+
-

Case 4 의 K

-
-
-
-
-
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료들.
1.
None
from : 과거의 어떤 생각이 이 생각을 만들었는가?
1.
2.
4.
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는가?
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는가?
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되고 이어지는가?
1.
참고 : 레퍼런스