그림 (참고4)
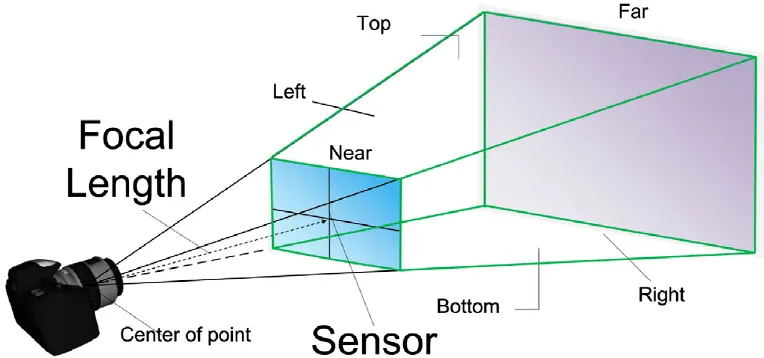
위 그림처럼 Left, Top, Bottom, Right 과 Near, Far 로 둘러싸인 각뿔대를 view volume 또는 viewing frustum (시야 사각뿔대: viewing  Frustum) 이라고 부른다.
Frustum) 이라고 부른다.
그림 (참고3)
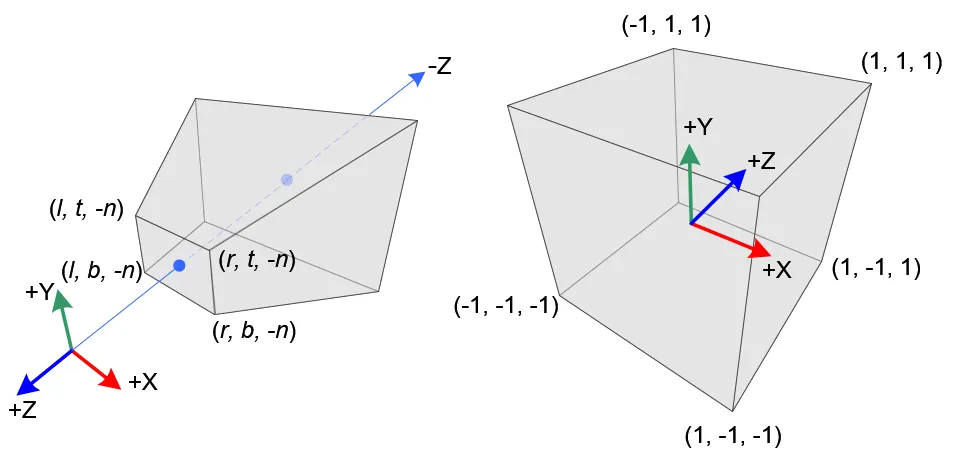
우리 눈 또는 카메라 는 위 그림 왼쪽 사각뿔대(Pyramid  Frustum) 형태의 공간에 있는 물체들에 대한 정보들을 near plane 이라는 2D 평면에 투영시킨다. Perspective projection (
Frustum) 형태의 공간에 있는 물체들에 대한 정보들을 near plane 이라는 2D 평면에 투영시킨다. Perspective projection ( Perspective Projection Transform) 은 이러한 사각뿔대 모양의 공간을(3D) 오른쪽 그림과 같은 직육면체 큐브(참고12,13:정육면체 아님) 공간(
Perspective Projection Transform) 은 이러한 사각뿔대 모양의 공간을(3D) 오른쪽 그림과 같은 직육면체 큐브(참고12,13:정육면체 아님) 공간( Canonical View Volume) 과 그 좌표계(
Canonical View Volume) 과 그 좌표계( Normalized Device Coordinate) 로(3D) 변환하는 것을 의미한다 (참고5, 6). 이때 Canonical View Volume 은 이름에도 나타나 있듯 정규화되어 (참고6) [-1, 1] 범위에만 존재한다 (참고12,13:Z방향은API 마다 다름). 이는 유연한 해상도 조절에 도움이 된다 (참고11).
Normalized Device Coordinate) 로(3D) 변환하는 것을 의미한다 (참고5, 6). 이때 Canonical View Volume 은 이름에도 나타나 있듯 정규화되어 (참고6) [-1, 1] 범위에만 존재한다 (참고12,13:Z방향은API 마다 다름). 이는 유연한 해상도 조절에 도움이 된다 (참고11).
분명히 projection 을 번역하면 ‘투영’ 이고, ‘투영’ 이란 3D 정보를 2D 로 구겨넣는 것을 의미하는데 (참고10:perspective projection transform vs homography vs perspective transform), perspective projection 이 3D → 3D 의 의미를 가진다니! 도대체 어찌된 일일까. 추측하기로는, 어차피 near plane 으로부터 변환(transform) 된 canonical view volume 의 한 면으로 volume 내 모든 좌표값을 정사영시키면 (z 값을 삭제해버리면) 바로 2D 정보를 얻어낼 수 있게 되기 때문에 사실상 2D 영상을 두 장 가지고 있다고 생각할 수 있을 것이라는 생각이 있지 않았을까. 물론 Projection 이라는 단어의 사전적 정의는 3D 를 2D 로 만드는 것이고 수학 및 컴퓨터비전에서는 3D → 2D 라는 투사과정에 주목하지만, 컴퓨터그래픽스에서는 평면처럼 보이지만 다시 3D 정보를 구해내야 할 경우에 대비한 reprojection 이나 depth testing (질문) 을 대비하여 (참고11) 3D → 2D 를 포함하는 3D → 3D 과정에 더 집중한다고 생각하면 편할 것 같다 (참고7, 13).
정리해 보면 이 projection 이라는 단어가 3D → 2D 과정을 의미하기도 하고, 3D → 3D 과정을 의미하는 것 같아 헷갈리는 것이 사실이지만 우리가 컴퓨터그래픽스를 다루는 동안에는 Perspective projection 이란 3D → 3D 과정이라는 것, (참고8) Perspective projection matrix 는 3D( Frustum)→3D(NDC) 변환을 표현한 행렬을 의미한다는 것을 기억하자.
Frustum)→3D(NDC) 변환을 표현한 행렬을 의미한다는 것을 기억하자.
이 카메라 좌표계(또는 눈 좌표계) 의 viewing frustum 에 perspective projection 이라는 것을 적용하여 NDC 의 canonical view volume 으로 매핑하면 어떤 일이 일어나는 것인지 아래 그림을 통해 시각적으로 알아보자.
그림 (참고9)
참고
5.