그림(ref5)
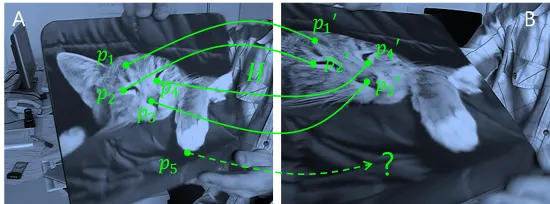
어느 위치에서 어느 방향으로 3D 물체를 바라보는지에 따라 그 모습이 달라진다는 사실을 모르는 사람은 없을 것이다. 카메라를 사용하는 경우도 마찬가지다. A, B는 같은 자세로 마우스패드를 잡고 있는 사람을 다른 위치와 다른 각도에서 촬영한 결과물이다. 과연 영상 A를 얻었을 때와 영상 B를 얻었을 각각의 경우 카메라는 어떻게 배치되어 있었을까? 이렇게 얻은 영상들의 형태는 다르지만 원래 동일한 피사체로부터 출발했다는 의미로 호모그래피(homography) 관계라고 불린다(ref4).
그림(ref3)
도로의 노면, TV 스크린, 유리창과 같이 평평해서 3차원 공간에 존재하지만 평면이라고 바라볼 수 있는 피사체를 ‘평평한 평면’( Planar Surface) 피사체라고 한다. 평평한 평면 피사체의 경우, 호모그래피 관계는 원근변환 또는 원근투영변환(
Planar Surface) 피사체라고 한다. 평평한 평면 피사체의 경우, 호모그래피 관계는 원근변환 또는 원근투영변환( Perspective Projection Transform)으로 표현가능하다.
Perspective Projection Transform)으로 표현가능하다.
평평한 평면 피사체 이야기가 나온 이유가 무엇일까? 호모그래피, 원근변환, 투시변환, 투영변환, 원근투영변환의 관계 때문이다. 이를 이해하기 위해서는 다양한 변환과 그 표현방식에 대해 살펴보아야 한다.
변환 | Transform |
원근(투시)변환 | Perspective Transform |
투영변환 | Projective Transform |
직교투영변환 | Orthographic Projection Transform |
원근투영변환 | Perspective Projection Transform |
몇몇 사람들은 원근변환과 투영변환이 동일한 것이라고 이야기하고, 투영변환이 원근투영변환과 같은 것이라고 이야기한다. 또 누군가는 투시변환과 투영변환이 동일한 것이라고 이야기한다. 여기에 호모그래피라는 단어까지 끼어들다 보니 머리가 복잡해진다. 하지만 내가 정리한 바에 따라 엄밀하게 따지면 원근변환과 투시변환이 같은 것일 뿐, 나머지는 모두 다른 개념을 의미하고 그 목적이 조금씩 다르다.
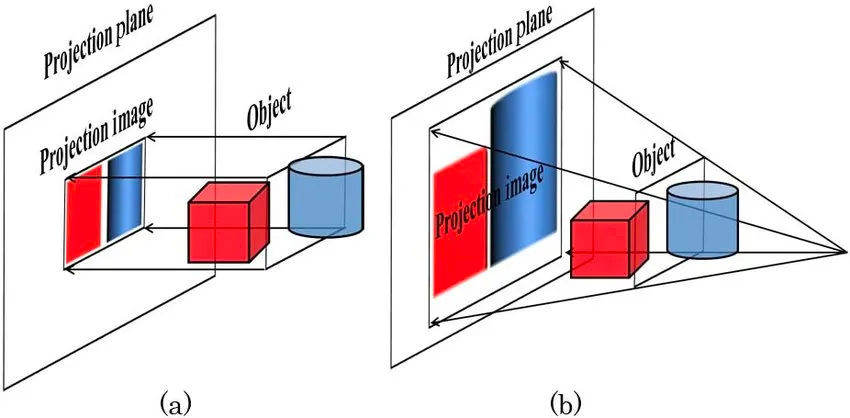
투영변환 먼저 살펴보자. 3D공간상의 물체를 2D로 투영하는 방식은 유일하지 않다. 대표적으로 잘 알려진 투영 방법은 두 가지로, 원근감을 반영하지 않은 직교투영(위 그림의 a)과 원근법을 적용한 원근투영(위 그림의 b)이다. 따라서 엄밀하게 따진다면 투영변환과 원근투영변환을 동급으로 두는 것은 옳지 않다. 투영변환은 직교투영변환과 원근투영변환을 모두 포함하기 때문이다. 하지만 대부분의 경우, 관습적으로 투영이라고 하면 원근투영을 떠올린다. 그래서 많은 사람들이 편하게 ‘원근투영변환’이라고 길게 쓰는 대신 ‘투영변환’이라고 쓴다(ref7). 하지만 이들을 잘 구분해두지 않으면 개념을 습득할 때 잔잔한 걸림돌이 된다. 이 글에서는 둘을 엄밀히 구분하기 위해 앞으로 원근변환과 원근투영변환이라는 표현을 구분해 사용하겠다.
그림 (ref8)
그 다음으로 살펴볼 것은 변환, 원근변환, 투영변환, 원근투영변환의 차이이다. 우리가 흔히 알고 있는 변환은 회전(Rotation), 평행이동(translation), 아핀(affine) 등의 변환이다. 이들과 마찬가지로 이 글에서 소개한 원근(투시)변환, 투영변환도 모두 일종의 변환이다. 여기서 [회전, 평행이동, 아핀, 원근] 변환과 투영변환을 나누는 기준은 차원이다. 전자들은 2D → 2D 또는 3D → 3D와 같이 차원이 유지되는 nD → nD 변환이라는 공통점이 있다. 후자는 투영이라는 단어가 시사하듯 원근투영변환이라는 단어는 3D → 2D와 같이 차원이 축소되는 변환임을 내포한다. 원근변환과 원근투영변환이 매우 비슷한 결과물을 낸다고 할지라도, 투영을 통한 차원 축소의 측면을 강조하고자 할 때에는 원근투영변환, 동일한 차원의 변환임을 강조하고자 할 때에는 원근변환이라고 표현하는 것이 좋다.
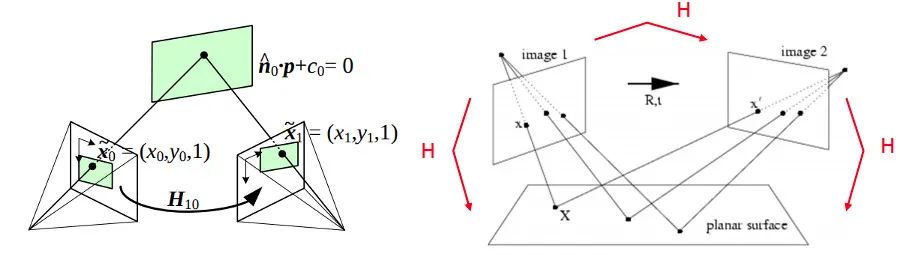
이렇게 개념이 정리되었다면 호모그래피, 원근(투시)변환, 원근투영변환의 관계를 평평한 평면 피사체 개념과 함께 설명할 수 있다. 취득한 영상들의 형태는 다르지만 원래 동일한 피사체로부터 출발했다는 것을 호모그래피 관계라고 표현하는데, 피사체는 3D 공간에 존재한다. 만약 3D 공간의 피사체가 2D 영상으로 차원이 축소되었다는 것을 강조하고자 할 때에는 원근투영변환이라는 표현을 사용한다. 한편 3D 공간의 피사체가 3차원 공간에 존재하지만 평면이라고 바라볼 수 있는 피사체인 평평한 평면 피사체라면 영상과 피사체 사이의 변환을 차원이 유지되는 변환이라고 볼 수 있고, 이 경우에는 호모그래피 또는 원근(투시)변환이라는 표현을 사용한다. 하나 더하면, 호모그래피라는 단어는 2D → 2D 변환인 경우에 사용되어(ref6) nD → nD (n > 2)인 변환을 표현할 때에는 호모그래피라는 단어를 잘 사용하지 않는 듯하다.
2D → 2D | 원근(투시)변환, 호모그래피 | perspective transform, homography |
3D → 2D | 원근투영변환 | perspective projection transform |
nD → nD | 원근(투시)변환 | perspective transform |
nD → (n-1)D | 원근투영변환 | perspective projection transform |
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료을 보관해 두는 영역입니다.
3.
from : 과거의 어떤 원자적 생각이 이 생각을 만들었는지 연결하고 설명합니다.
1.
•
NDC라는 개념을 학습할 때 원근(투시)변환, 원근투영변환, 호모그래피 등의 개념들이 정확히 잡혀 있지 않아 이해하는 데 시간이 오래 걸렸다.
2.
•
앞의 글에서는 아핀 변환에 대해 설명한다.
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는지 연결합니다.
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는지 연결합니다.
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되거나 이어지는지를 작성하는 영역입니다.
1.
None
ref : 생각에 참고한 자료입니다.
6.