그림(ref2)
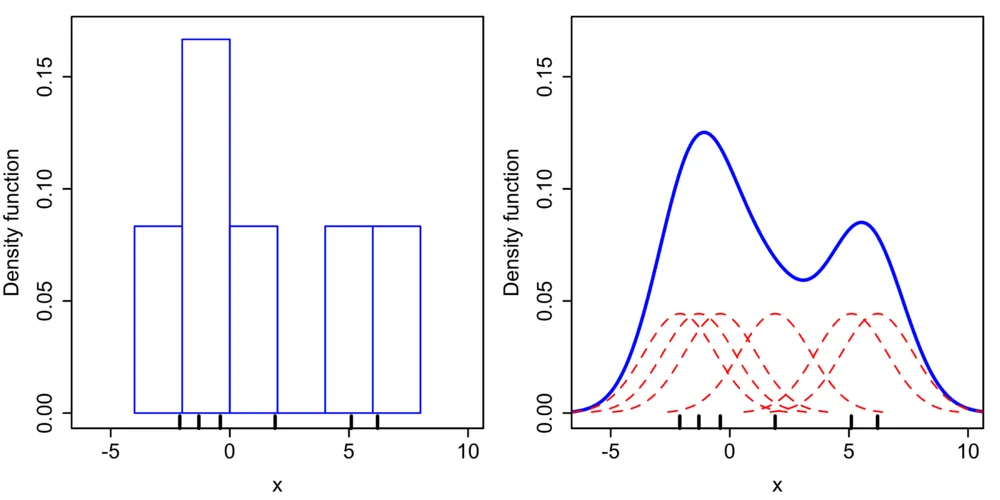
히스토그램은 이산적인 데이터를 적당한 구간으로 나누고 해당 구간 안에 포함되는 데이터포인트들의 개수를 세어 만들어낸 분포 시각화를 의미한다(ref3). 예를 들어 나와 친한 10명의 친구들의 키를 수집하고, 친구들의 키를 5cm 구간으로 나누어 시각화하면 그림(ref2)의 왼쪽과 같은 히스토그램을 만들 수 있다.
그런데 나는 저렇게 삐죽거리는 히스토그램이 딱히 마음에 들지 않는다. 아무리 훌륭하게 구간을 나누어도, 구간의 경계에서 불연속성을 띤다. 히스토그램이 이렇게 삐죽거릴수밖에 없는 이유의 본질에는 자연에서 추출해 관측한 데이터의 개수가 유한하기 때문이다. 이러한 히스토그램을 사용하지 않고 그림(ref2)의 오른쪽 파란색 그래프같이 연속 함수로 스무스하게 데이터를 표현하고 싶다면 어떻게 해야 할까?(ref6)
이산적으로 관측된 각각의 데이터 포인트들을, 관측된 데이터 포인트를 중심으로 서서히 줄어드는 안개의 일종으로 보는 것이다(ref4). 마치 그림(ref2) 중 오른쪽 그래프에 보이는 빨간 점선처럼 말이다. 정규분포와 같이 좌우 대칭이고 연속인 함수가 빨간 점선의 후보로 많이 사용된다. 우리는 고등학교 때, 연속함수와 연속함수를 더하면 연속함수가 된다는 사실을 배웠다. 빨간 점선 각각을 함수로 보고, 이들 함수를 모두 더하면 파란색 분포를 만들어줄 수 있다.
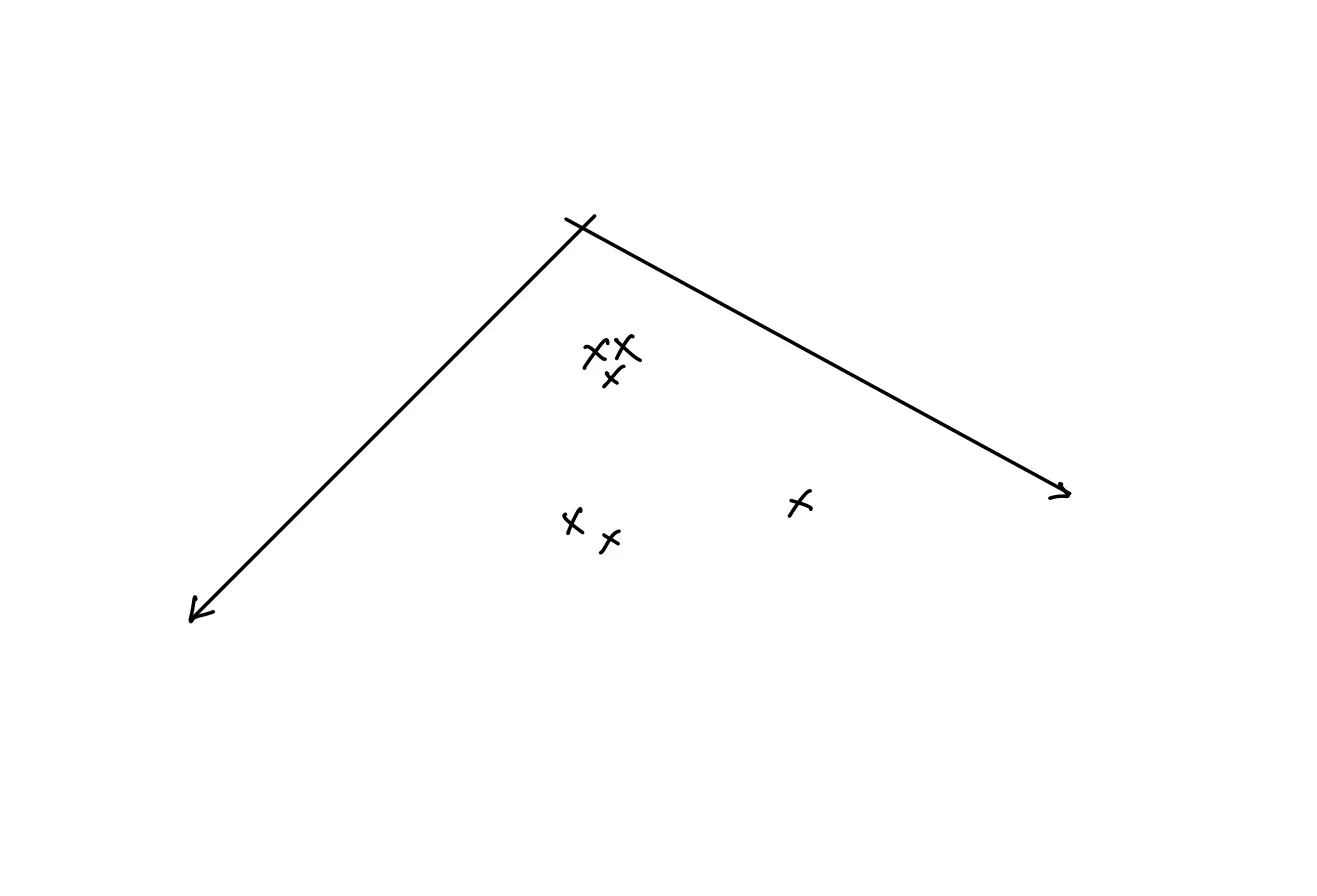
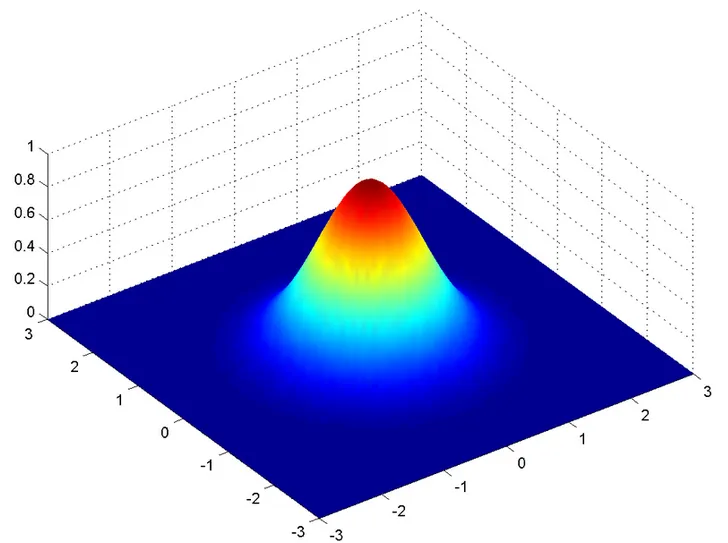
이는 비단 위와 같은 1D 데이터 분포에만 사용할 수 있는 것은 아니다. 2D 의 경우에도 동일한 논리가 적용된다. 위와 같이 퍼져 있는 각각의 점들에 아래 그림과 같은 형태의 분포가 할당되어 있다고 생각해 보자.
그림(ref1)
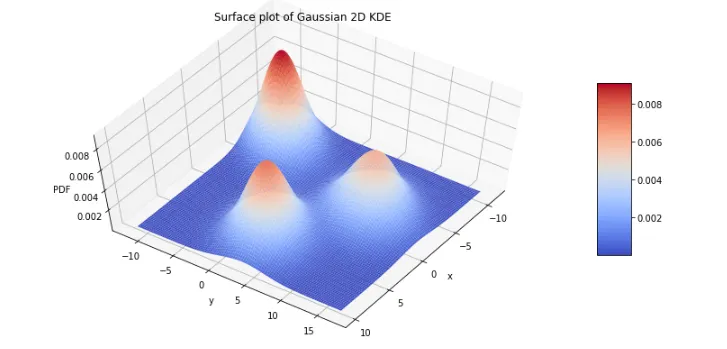
그림(ref5): 형태만 보고 x, y, z 축의 값을 신경쓰지는 말자.
이번에는 그림(ref1)에 보이는 연속함수 이 그림(ref2)의 오른쪽 빨간 점선같은 존재가 된다. 각각의 이산적인 점을 연속함수로 보고 전부 더하면, 그림(ref5)와 같은 결과를 얻을 수 있다.
parse me : 언젠가 이 글에 쓰이면 좋을 것 같은 재료을 보관해 두는 영역입니다.
1.
None
from : 과거의 어떤 원자적 생각이 이 생각을 만들었는지 연결하고 설명합니다.
1.
2.
•
나중에 보니 Mean Shift Algorithm은 KDE의 일종이었다(ref7,ref8).
supplementary : 어떤 새로운 생각이 이 문서에 작성된 생각을 뒷받침하는지 연결합니다.
1.
None
opposite : 어떤 새로운 생각이 이 문서에 작성된 생각과 대조되는지 연결합니다.
1.
None
to : 이 문서에 작성된 생각이 어떤 생각으로 발전되거나 이어지는지를 작성하는 영역입니다.
ref : 생각에 참고한 자료입니다.